2.6.3 有理数加减混合运算的实际应用 课件(共12张PPT)
文档属性
| 名称 | 2.6.3 有理数加减混合运算的实际应用 课件(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1002.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 06:48:04 | ||
图片预览





文档简介
(共12张PPT)
北师大版 七年级上册
第二章 有理数及其运算
6 有理数的加减混合运算
第3课时 有理数加减混合运算的实际应用
导入新课
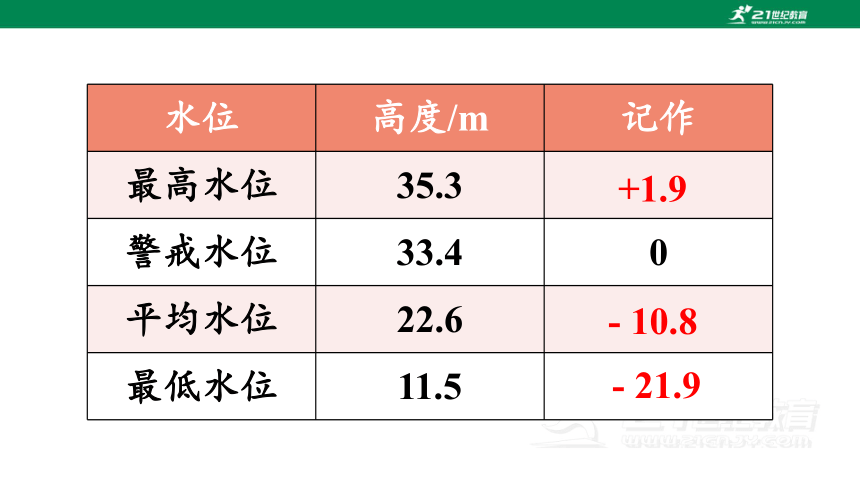
右图是流花河的水文资料(单位:m),取河流的警戒水位作为 0 点,那么图中的其他数据可以分别记作什么?
35.3
33.4
22.6
11.5
流花河水位
最高水位
警戒水位
平均水位
最低水位
水位 高度/m 记作
最高水位 35.3
警戒水位 33.4 0
平均水位 22.6
最低水位 11.5
+1.9
- 10.8
- 21.9
探究新知
探究
下表是某水位站记录的潮汛期某河流一周内的水位变化情况(“+”号表示水位比前一天上升,“-”号表示水位比前一天下降,上周末的水位恰好达到警戒水位.单位:m)
星期 一 二 三 四 五 六 日
水位变 化/m 0.20 0.81 -0.35 0.13 0.28 -0.36 -0.01
(1)本周哪一天河流水位最高,哪一天河流水位最低,它们位于警戒水位之上还是之下,与警戒水位的距离分别是多少?
(2)与上周末相比,本周末河流的水位是上升还是下降了?
(3)完成本周水位记录表.
星期 一 二 三 四 五 六 日
水位变 化/m 0.20 0.81 -0.35 0.13 0.28 -0.36 -0.01
解:(1)前两天的水位是上升的,第1天的水位是+0.20 m;
第2天的水位是+0.20+0.81=+1.01(m);
第3天的水位是+1.01-0.35=+0.66(m);
第4天的水位是+0.66+0.13=+0.79(m);
第5天的水位是0.79+0.28=+1.07(m);
第6天的水位是1.07-0.36=+0.71(m);
第7天的水位是0.71-0.01=+0.7(m);
则水位最低的是第一天,高于警戒水位;水位最高的是第5天;
(2)+0.20+0.81-0.35+0.13+0.28-0.36-0.01=+0.7(m),则本周末河流的水位上升了0.7 m;
(3)如下表:
星期 一 二 三 四 五 六 日
水位变 化/m 33.6 34.41 34.06 34.19 34.47 34.11 34.1
应用举例
例1 光明中学七(1)班学生的平均身高是160 cm.
(1)下表给出了该班6名学生的身高情况(单位:cm).试完成下表:
姓名 小明 小彬 小丽 小亮 小颖 小山
身高 159 162 160 154 163 165
身高与平均 身高的差值
(2)这6名学生中谁最高?谁最矮?
(3)最高与最矮的学生身高相差多少?
解:(2)小山最高,小亮最矮;
(3)最高与最矮的学生身高相差5-(-6)=11(cm).
-1
+2
0
-6
+3
+5
例2 下表为某个雨季某水库管理员记录的水库一周内的水位变化情况,警戒水位为15 m(上周末的水位达到警戒水位).
星期 一 二 三 四 五 六 日
水位变化/m +0.38 +0.25 +0.54 +0.13 -0.45 +0.36 -0.19
注:正数表示比前一天水位上升,负数表示比前一天水位下降.
(1)本周哪一天水位最高?有多少米?
(2)根据给出的数据,请利用折线统计图分析本周内该水库的水位变化情况(在不放水的情况下).
解:(1)星期四水位最高为(+0.38+0.25+0.54+0.13)+15=16.3(m);
(2)由已知条件,可求出一周内各天相对于警戒水位的变化情况,列表如下:
星期 一 二 三 四 五 六 日
水位变化/m +0.38 +0.63 +1.17 +1.30 +0.85 +1.21 +1.02
以警戒水位为0点,用折线统计图表示在不放水的情况下该水库一周内的水位变化情况如图所示.
随堂练习
1.某天上午6:00柳江河水位为80.4 m,到上午11:30水位上涨了3.2 m,到下午6:00水位又跌了2.1 m,则下午6:00水位应为( )
A.76 m B.85.7 m C.81.5 m D.86.8 m
2.某地一天早晨的气温是-5 ℃,中午上升了9 ℃,午夜又下降了7 ℃,则午夜的气温是( )
A.-3 ℃ B.-5 ℃ C.5 ℃ D.-9 ℃
C
A
3.现有10包棉签,以每包100根为标准,超过的根数记作正数,不足的根数记作负数,每包的数据记录如下(单位:根):
+3,-2,-1,0,+5,-1,+4,-2,-5,+2.
回答下列问题:
(1)这10包棉签中根数最多的有____根,最少的有____根;
(2)这10包棉签一共有多少根?
解:(+3)+(-2)+(-1)+0+(+5)+(-1)+(+4)+(-2)+
(-5)+(+2)=3(根),100×10+3=1 003(根).
答:这10包棉签一共有1 003根.
105
95
北师大版 七年级上册
第二章 有理数及其运算
6 有理数的加减混合运算
第3课时 有理数加减混合运算的实际应用
导入新课
右图是流花河的水文资料(单位:m),取河流的警戒水位作为 0 点,那么图中的其他数据可以分别记作什么?
35.3
33.4
22.6
11.5
流花河水位
最高水位
警戒水位
平均水位
最低水位
水位 高度/m 记作
最高水位 35.3
警戒水位 33.4 0
平均水位 22.6
最低水位 11.5
+1.9
- 10.8
- 21.9
探究新知
探究
下表是某水位站记录的潮汛期某河流一周内的水位变化情况(“+”号表示水位比前一天上升,“-”号表示水位比前一天下降,上周末的水位恰好达到警戒水位.单位:m)
星期 一 二 三 四 五 六 日
水位变 化/m 0.20 0.81 -0.35 0.13 0.28 -0.36 -0.01
(1)本周哪一天河流水位最高,哪一天河流水位最低,它们位于警戒水位之上还是之下,与警戒水位的距离分别是多少?
(2)与上周末相比,本周末河流的水位是上升还是下降了?
(3)完成本周水位记录表.
星期 一 二 三 四 五 六 日
水位变 化/m 0.20 0.81 -0.35 0.13 0.28 -0.36 -0.01
解:(1)前两天的水位是上升的,第1天的水位是+0.20 m;
第2天的水位是+0.20+0.81=+1.01(m);
第3天的水位是+1.01-0.35=+0.66(m);
第4天的水位是+0.66+0.13=+0.79(m);
第5天的水位是0.79+0.28=+1.07(m);
第6天的水位是1.07-0.36=+0.71(m);
第7天的水位是0.71-0.01=+0.7(m);
则水位最低的是第一天,高于警戒水位;水位最高的是第5天;
(2)+0.20+0.81-0.35+0.13+0.28-0.36-0.01=+0.7(m),则本周末河流的水位上升了0.7 m;
(3)如下表:
星期 一 二 三 四 五 六 日
水位变 化/m 33.6 34.41 34.06 34.19 34.47 34.11 34.1
应用举例
例1 光明中学七(1)班学生的平均身高是160 cm.
(1)下表给出了该班6名学生的身高情况(单位:cm).试完成下表:
姓名 小明 小彬 小丽 小亮 小颖 小山
身高 159 162 160 154 163 165
身高与平均 身高的差值
(2)这6名学生中谁最高?谁最矮?
(3)最高与最矮的学生身高相差多少?
解:(2)小山最高,小亮最矮;
(3)最高与最矮的学生身高相差5-(-6)=11(cm).
-1
+2
0
-6
+3
+5
例2 下表为某个雨季某水库管理员记录的水库一周内的水位变化情况,警戒水位为15 m(上周末的水位达到警戒水位).
星期 一 二 三 四 五 六 日
水位变化/m +0.38 +0.25 +0.54 +0.13 -0.45 +0.36 -0.19
注:正数表示比前一天水位上升,负数表示比前一天水位下降.
(1)本周哪一天水位最高?有多少米?
(2)根据给出的数据,请利用折线统计图分析本周内该水库的水位变化情况(在不放水的情况下).
解:(1)星期四水位最高为(+0.38+0.25+0.54+0.13)+15=16.3(m);
(2)由已知条件,可求出一周内各天相对于警戒水位的变化情况,列表如下:
星期 一 二 三 四 五 六 日
水位变化/m +0.38 +0.63 +1.17 +1.30 +0.85 +1.21 +1.02
以警戒水位为0点,用折线统计图表示在不放水的情况下该水库一周内的水位变化情况如图所示.
随堂练习
1.某天上午6:00柳江河水位为80.4 m,到上午11:30水位上涨了3.2 m,到下午6:00水位又跌了2.1 m,则下午6:00水位应为( )
A.76 m B.85.7 m C.81.5 m D.86.8 m
2.某地一天早晨的气温是-5 ℃,中午上升了9 ℃,午夜又下降了7 ℃,则午夜的气温是( )
A.-3 ℃ B.-5 ℃ C.5 ℃ D.-9 ℃
C
A
3.现有10包棉签,以每包100根为标准,超过的根数记作正数,不足的根数记作负数,每包的数据记录如下(单位:根):
+3,-2,-1,0,+5,-1,+4,-2,-5,+2.
回答下列问题:
(1)这10包棉签中根数最多的有____根,最少的有____根;
(2)这10包棉签一共有多少根?
解:(+3)+(-2)+(-1)+0+(+5)+(-1)+(+4)+(-2)+
(-5)+(+2)=3(根),100×10+3=1 003(根).
答:这10包棉签一共有1 003根.
105
95
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
