12.3 角的平分线的性质(第1课时)课件
文档属性
| 名称 | 12.3 角的平分线的性质(第1课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 320.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-28 18:37:10 | ||
图片预览


文档简介
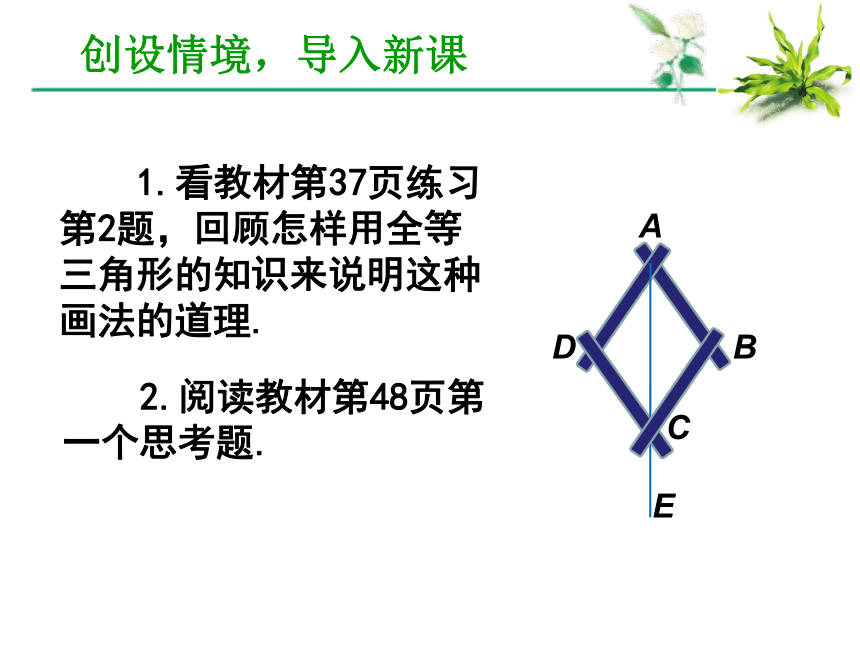
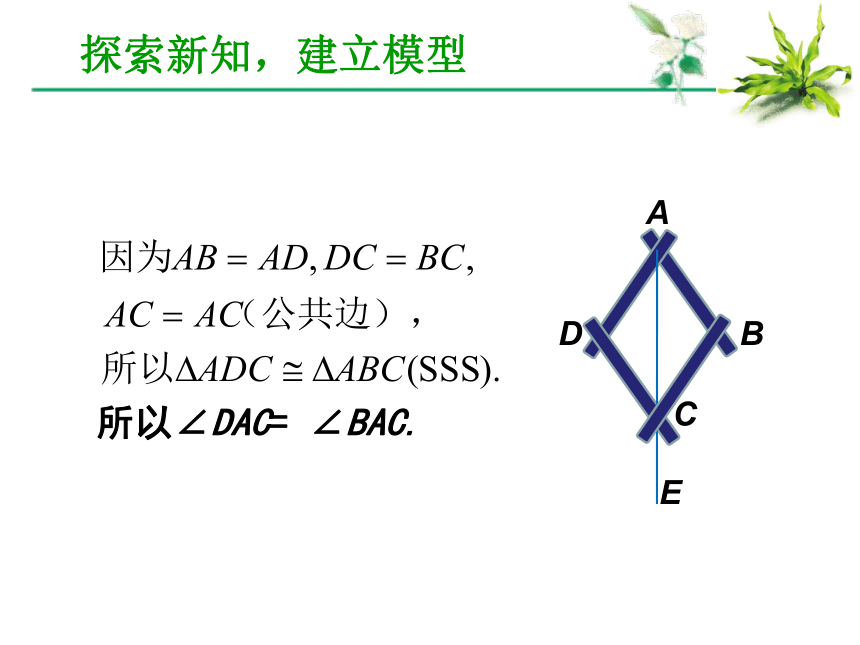
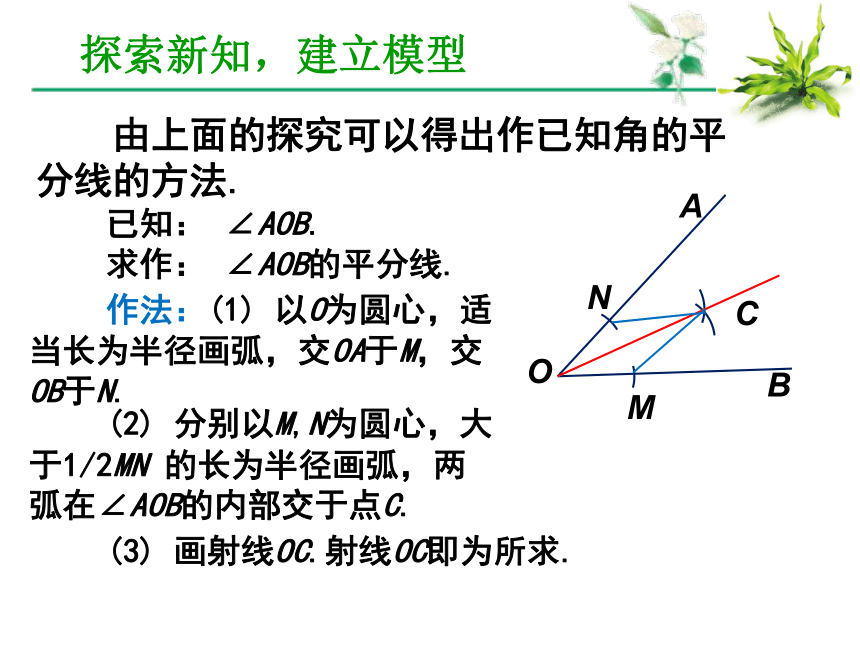
课件11张PPT。第十二章 全等三角形创设情境,导入新课 1.看教材第37页练习第2题,回顾怎样用全等三角形的知识来说明这种画法的道理. 2.阅读教材第48页第一个思考题.DCBAE探索新知,建立模型DCBAE所以∠DAC= ∠BAC.探索新知,建立模型 由上面的探究可以得出作已知角的平分线的方法. 已知: ∠AOB. 求作: ∠AOB的平分线. 作法:(1) 以O为圆心,适当长为半径画弧,交OA于M,交OB于N. (2) 分别以M,N为圆心,大于1/2MN 的长为半径画弧,两弧在∠AOB的内部交于点C. (3) 画射线OC.射线OC即为所求.OCBAMN探索新知,建立模型 练一练教材第51页习题12.3第1题.看一看 角平分线的性质.gsp 试一试 角平分线的识别.gsp角平分线的判定:探索新知,建立模型 角的平分线上的点到角的两边的距离相等.角平分线的性质: 角的内部到角的两边的距离相等的点在角的平分线上.探索新知,建立模型 一般情况下,我们要证明一个几何中的命题时,会按照类似的步骤进行,即(1)明确命题中的已知和求证;(2)根据题意,画出图形,并用数学符号表示已知和求证;(3)经过分析,找出由已知推出求证的途径,写出证明过程. 如图, ∠AOC = ∠BOC,点P在OC上,PD⊥OA,
PE⊥OB,垂足分别为点D,E.求证PD=PE. 探索新知,建立模型证明:∵PD⊥OA,PE⊥OB,∴ ∠PDO = ∠PEO=90°.在△PDO和△PEO中,∠PDO = ∠PEO,∠DOP = ∠EOP,OP = OP,∴ △PDO ≌ △PEO(AAS).∴ PD = PE.OPBAEDC解析、应用与拓展 1.(教材第49页思考题) 分析:把公路、铁路看成两条相交线,先作其角的平分线OB(O为顶点),再在OB上作OS,使OS=2.5 cm,点S 即为所求. 2.如图,在△ABC 中, ∠C =90°,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离DE长为多少? 3.你能用尺规作出一个45°的角吗?OSBAEDC (3)证明一个文字几何命题一般分三步走. (1)本节课学到了哪些角平分线的知识?小结归纳 (2)角平分线有多种画法(借助量角器、透明纸、角尺、平分角的仪器等),但尺规作图最佳,作图的道理可以通过三角形全等的证明来获得.布置作业 1.必做题:
(1)教材第51页习题12.3第 2、4题.
(2)教材第56页复习题12第 13题. 2.选做题:
(1)教材第55页复习题12第 5题.
(2)作一个三角形三个内角的平分线,你发现了什么?与同伴进行交流.
PE⊥OB,垂足分别为点D,E.求证PD=PE. 探索新知,建立模型证明:∵PD⊥OA,PE⊥OB,∴ ∠PDO = ∠PEO=90°.在△PDO和△PEO中,∠PDO = ∠PEO,∠DOP = ∠EOP,OP = OP,∴ △PDO ≌ △PEO(AAS).∴ PD = PE.OPBAEDC解析、应用与拓展 1.(教材第49页思考题) 分析:把公路、铁路看成两条相交线,先作其角的平分线OB(O为顶点),再在OB上作OS,使OS=2.5 cm,点S 即为所求. 2.如图,在△ABC 中, ∠C =90°,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离DE长为多少? 3.你能用尺规作出一个45°的角吗?OSBAEDC (3)证明一个文字几何命题一般分三步走. (1)本节课学到了哪些角平分线的知识?小结归纳 (2)角平分线有多种画法(借助量角器、透明纸、角尺、平分角的仪器等),但尺规作图最佳,作图的道理可以通过三角形全等的证明来获得.布置作业 1.必做题:
(1)教材第51页习题12.3第 2、4题.
(2)教材第56页复习题12第 13题. 2.选做题:
(1)教材第55页复习题12第 5题.
(2)作一个三角形三个内角的平分线,你发现了什么?与同伴进行交流.
