1.3 勾股定理的应用 课件(共18张PPT)
文档属性
| 名称 | 1.3 勾股定理的应用 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
北师大版 八年级上册
第一章 勾股定理
3 勾股定理的应用
导入新课
多媒体投影图片,引出问题:有一块长方形绿地,绿地周边是小路,在绿地旁边的B处有健身器材.居住在A处的居民为了走近路而不惜践踏草地直接从A到B.
问题1:各位同学,你知道他们为什么不走绿地周边的小路吗?
问题2:如图,假设入口A到拐角C处3m,拐角C到健身器材B处4m,你能计算出小草受伤的代价是他们少走几步吗?(假设2步为1m)
解:AB2=AC2+BC2=32+42=25,AB=5m,5×2=10(步).
3+4=7(m),7×2=14(步).
14-10=4(步).
探究新知
探究
李叔叔想要检测如图所示的雕塑底座正面的边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺.
连接对角线AC,只要分别量出AB、BC、AC的长度即可.
AB2+BC2=AC2
△ABC为直角三角形
(1)你能替他想办法完成任务吗?
(2)李叔叔量得边AD长是30cm,边AB长是40cm,点B,D之间的距离是50cm.边AD垂直于边AB吗?
在△ABD中,AD=30cm,AB=40cm,BD=50cm,
因为AD2+AB2=302+402
=900+1600=2500,
BD2=502=2500,
所以AD2+AB2=BD2,
所以△ABD是直角三角形,
所以∠DAB=90°
所以AD⊥AB .
(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验边AD是否垂直于边AB吗?边BC与边AB呢?
测量方法不唯一;
例如在AD边上测量一段AE=6cm,在AB边上测量一段AF=8cm,
再测量点E,F两点间的距离EF,
若EF=10cm,
由AE2+AF2=62+82=36+64=100=EF2,可知△AEF是直角三角形,且∠EAF=90°,
∴DA⊥AB.边BC与边AB是否垂直可以用类似的方法测量.
探究新知
探究
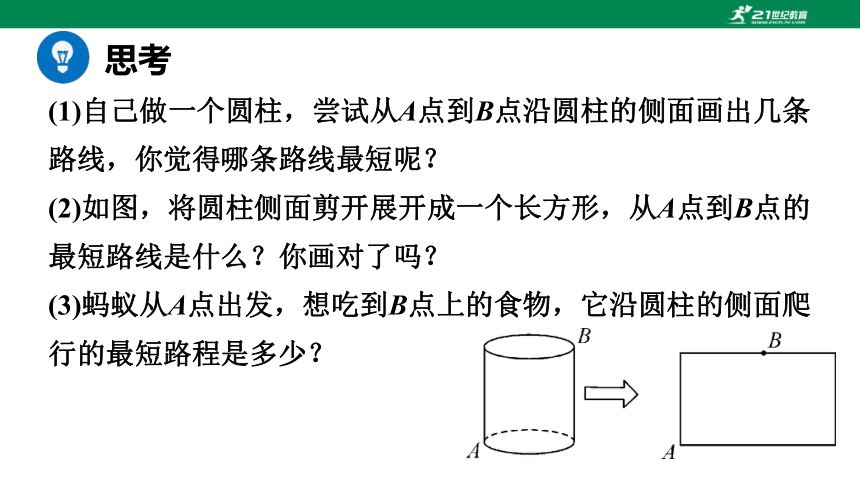
有一个圆柱,它的高等于12厘米,底面半径等于3厘米.在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是多少?(π的取值3)
A
B
(1)自己做一个圆柱,尝试从A点到B点沿圆柱的侧面画出几条路线,你觉得哪条路线最短呢?
(2)如图,将圆柱侧面剪开展开成一个长方形,从A点到B点的最短路线是什么?你画对了吗?
(3)蚂蚁从A点出发,想吃到B点上的食物,它沿圆柱的侧面爬行的最短路程是多少?
思考
现在就用剪刀沿母线AA′将圆柱的侧面展开(如下图).
我们不难发现几走法:
(1) A→A′→B; (2) A→B′→B;
(3) A→D→B; (4) A→B.
哪条路线是最短呢?
第(4)条路线A→B最短.
因为“两点之间的连线中线段最短”.
蚂蚁怎么走最近?
【归纳结论】
B
A
B
A
d
A
B
A'
A
B
B
A
O
A'
√
若已知圆柱体高为12 cm,底面半径为3 cm,π取3,则:
B
A
3
O
12
侧面展开图
12
3π
A
B
方法归纳:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
A'
A'
∴AB=15
应用举例
例1 下图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长.
A
E
B
C
D
解:设滑道AC的长度为xm,则AB的长度为xm,AE的长度为(x-1)m.
在Rt△ACE中,∠AEC=90°,
由勾股定理得 AE2+CE2=AC2,
即(x-1)2+32=x2,解得x=5.
故滑道AC的长度为5m.
例2 如图,一个无盖的长方体盒子的长、宽、高分别为8cm,8cm,12cm,一只蚂蚁想从盒底的点A处沿盒的表面爬到盒顶的点B处,你能帮蚂蚁设计一条最短的路线吗?蚂蚁要爬行的最短路程是多少?
解:当蚂蚁沿前面和上底面爬行时,最短路线如答图①所示.
此时,AC=8cm,BC=12+8=20(cm).
AB2=AC2+BC2=82+202=464.
当蚂蚁沿前面和侧面爬行时,最短路线如答图②所示.
此时,AD=8+8=16(cm),BD=12cm.
AB2=AD2+BD2=162+122=400,AB=20cm.
∵464>400,
∴蚂蚁爬行的最短路线为答图②的线段AB,要爬行的最短路程是20cm.
课堂小结
勾股定理的应用
立体图形中两点之间的最短距离
勾股定理的实际应用
随堂练习
1.小雨用竹竿扎了一个长40cm、宽30cm的长方形框架,由于四边形容易变形,需要用一根竹竿作斜拉杆将四边形定形,则斜拉杆最长需____cm.
50
2.如图,有两棵树,一棵高13m,另一棵高8m,两树相距12m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了____m.
13
3.如图,阴影部分的半圆的面积是多少?(π取3.14)
北师大版 八年级上册
第一章 勾股定理
3 勾股定理的应用
导入新课
多媒体投影图片,引出问题:有一块长方形绿地,绿地周边是小路,在绿地旁边的B处有健身器材.居住在A处的居民为了走近路而不惜践踏草地直接从A到B.
问题1:各位同学,你知道他们为什么不走绿地周边的小路吗?
问题2:如图,假设入口A到拐角C处3m,拐角C到健身器材B处4m,你能计算出小草受伤的代价是他们少走几步吗?(假设2步为1m)
解:AB2=AC2+BC2=32+42=25,AB=5m,5×2=10(步).
3+4=7(m),7×2=14(步).
14-10=4(步).
探究新知
探究
李叔叔想要检测如图所示的雕塑底座正面的边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺.
连接对角线AC,只要分别量出AB、BC、AC的长度即可.
AB2+BC2=AC2
△ABC为直角三角形
(1)你能替他想办法完成任务吗?
(2)李叔叔量得边AD长是30cm,边AB长是40cm,点B,D之间的距离是50cm.边AD垂直于边AB吗?
在△ABD中,AD=30cm,AB=40cm,BD=50cm,
因为AD2+AB2=302+402
=900+1600=2500,
BD2=502=2500,
所以AD2+AB2=BD2,
所以△ABD是直角三角形,
所以∠DAB=90°
所以AD⊥AB .
(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验边AD是否垂直于边AB吗?边BC与边AB呢?
测量方法不唯一;
例如在AD边上测量一段AE=6cm,在AB边上测量一段AF=8cm,
再测量点E,F两点间的距离EF,
若EF=10cm,
由AE2+AF2=62+82=36+64=100=EF2,可知△AEF是直角三角形,且∠EAF=90°,
∴DA⊥AB.边BC与边AB是否垂直可以用类似的方法测量.
探究新知
探究
有一个圆柱,它的高等于12厘米,底面半径等于3厘米.在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是多少?(π的取值3)
A
B
(1)自己做一个圆柱,尝试从A点到B点沿圆柱的侧面画出几条路线,你觉得哪条路线最短呢?
(2)如图,将圆柱侧面剪开展开成一个长方形,从A点到B点的最短路线是什么?你画对了吗?
(3)蚂蚁从A点出发,想吃到B点上的食物,它沿圆柱的侧面爬行的最短路程是多少?
思考
现在就用剪刀沿母线AA′将圆柱的侧面展开(如下图).
我们不难发现几走法:
(1) A→A′→B; (2) A→B′→B;
(3) A→D→B; (4) A→B.
哪条路线是最短呢?
第(4)条路线A→B最短.
因为“两点之间的连线中线段最短”.
蚂蚁怎么走最近?
【归纳结论】
B
A
B
A
d
A
B
A'
A
B
B
A
O
A'
√
若已知圆柱体高为12 cm,底面半径为3 cm,π取3,则:
B
A
3
O
12
侧面展开图
12
3π
A
B
方法归纳:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
A'
A'
∴AB=15
应用举例
例1 下图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长.
A
E
B
C
D
解:设滑道AC的长度为xm,则AB的长度为xm,AE的长度为(x-1)m.
在Rt△ACE中,∠AEC=90°,
由勾股定理得 AE2+CE2=AC2,
即(x-1)2+32=x2,解得x=5.
故滑道AC的长度为5m.
例2 如图,一个无盖的长方体盒子的长、宽、高分别为8cm,8cm,12cm,一只蚂蚁想从盒底的点A处沿盒的表面爬到盒顶的点B处,你能帮蚂蚁设计一条最短的路线吗?蚂蚁要爬行的最短路程是多少?
解:当蚂蚁沿前面和上底面爬行时,最短路线如答图①所示.
此时,AC=8cm,BC=12+8=20(cm).
AB2=AC2+BC2=82+202=464.
当蚂蚁沿前面和侧面爬行时,最短路线如答图②所示.
此时,AD=8+8=16(cm),BD=12cm.
AB2=AD2+BD2=162+122=400,AB=20cm.
∵464>400,
∴蚂蚁爬行的最短路线为答图②的线段AB,要爬行的最短路程是20cm.
课堂小结
勾股定理的应用
立体图形中两点之间的最短距离
勾股定理的实际应用
随堂练习
1.小雨用竹竿扎了一个长40cm、宽30cm的长方形框架,由于四边形容易变形,需要用一根竹竿作斜拉杆将四边形定形,则斜拉杆最长需____cm.
50
2.如图,有两棵树,一棵高13m,另一棵高8m,两树相距12m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了____m.
13
3.如图,阴影部分的半圆的面积是多少?(π取3.14)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
