5.4 应用二元一次方程组——增收节支 课件(共14张PPT)
文档属性
| 名称 | 5.4 应用二元一次方程组——增收节支 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 655.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 15:43:16 | ||
图片预览






文档简介
(共14张PPT)
第五章 二元一次方程组
4 应用二元一次方程组
——增收节支
北师版 八年级 数学(上)
导入新课
在现实生活中,我们常常会听到这样一个词语:增收节支.当我们遇到实际问题的时候,该如何解决呢?
例如:某工厂去年的利润(总收入-总支出)为200万元.今年总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总收入、总支出各是多少万元
如果设去年的总产值为x万元,总支出为y万元.
你能否采用表格的形式,用x,y的代数式来表示题目中的各个量呢?
探究新知
探究
1.找出问题中的等量关系
去年的总收入 - 去年的总支出 =200万元
今年的总收入 - 今年的总支出 =780万元
2:填表:设去年的总收入为x万元,总支出为y万元,则有:
总收入/万元 总支出/万元 利润/万元
去年
今年
x
y
200
(1+20%)x
(1-10%)y
780
3:正确书写解题过程
解:设去年的总收入为x万元,总支出为y万元,则今年的总收入为(1+20%)x万元,今年的总支出为(1-10%)y万元.
根据题意,得
解得
答:去年的总收入为2 000万元,总支出为1 800万元.
x-y=200,
(1+20%) x - (1 - 10%) y=780.
x=2000, y=1800.
应用举例
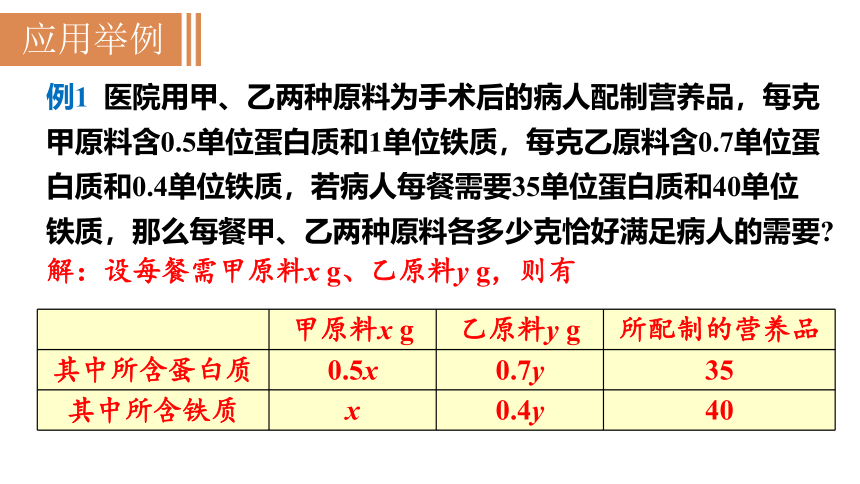
例1 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质,若病人每餐需要35单位蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰好满足病人的需要
解:设每餐需甲原料x g、乙原料y g,则有
甲原料x g 乙原料y g 所配制的营养品
其中所含蛋白质 0.5x 0.7y 35
其中所含铁质 x 0.4y 40
根据上表,可以列出方程组 ,
解得 .
所以每餐需甲原料28g、乙原料30g.
0.5x+0.7y=35
x+0.4y=40
x=28
y=30
例2 我区某学校原计划向内蒙古察右旗地区的学生捐赠3 500册图书,实际共捐赠了4 125册,其中初中学生捐赠了原计划的120%,高中学生捐赠了原计划的115%,初中学生和高中学生各比原计划多捐赠图书多少册?
解:设原计划初中学生捐x册,高中学生捐y册,填写下表.
初中学生捐的数量 高中学生捐的数量 合计
计划
实际
x
y
3 500
120%x
115%y
4 125
根据上表列方程组,得
解得
初中学生比原计划多捐的册数是2 000×(120%-1)=400(册),
高中学生比原计划多捐的册数是1 500×(115%-1)=225(册),
答:初中学生和高中学生各比原计划多捐赠图书400册和225册.
x+y=3500,
120%x+115 % y=4125.
x=2000, y=1500.
课堂小结
列方程组解决实际问题
增长率、利润问题
利用图表分析等量关系
随堂练习
1.某市现有人口45万,计划一年后城镇人口增加0.7%,农村人口增加1.2%,这样,全市人口将增加1%,求这个市现在的城镇人口与农村人口.设现在城镇人口有x万,农村人口有y万,则下列方程组中正确的是( )
B
2.将浓度为30%的酒精与浓度为60%的酒精混合,制成了浓度为50%的酒精30 kg.设浓度为30%的酒精需要x kg,浓度为60%的酒精需要y kg,则列出的方程组为
—————————————.
x+y=30,
30%x+60 % y=50 %×30
3.今年“五一”小长假期间,某市外来与外出旅游的总人数为226万人,分别比去年同期增长30%和20%,去年同期外来旅游比外出旅游的人数多20万人.求该市今年外来和外出旅游的人数.
解:设去年外来旅游的人数为x万人,外出旅游的人数为y万人.
根据题意,得 解得
所以(1+30%)x=(1+30%)×100=130,
(1+20%)y=(1+20%)×80=96.
答:该市今年外来和外出旅游的人数分别是130万人和96万人.
x-y=20,
(1+30%)x+(1+20%) y=226.
x=100, y=80.
第五章 二元一次方程组
4 应用二元一次方程组
——增收节支
北师版 八年级 数学(上)
导入新课
在现实生活中,我们常常会听到这样一个词语:增收节支.当我们遇到实际问题的时候,该如何解决呢?
例如:某工厂去年的利润(总收入-总支出)为200万元.今年总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总收入、总支出各是多少万元
如果设去年的总产值为x万元,总支出为y万元.
你能否采用表格的形式,用x,y的代数式来表示题目中的各个量呢?
探究新知
探究
1.找出问题中的等量关系
去年的总收入 - 去年的总支出 =200万元
今年的总收入 - 今年的总支出 =780万元
2:填表:设去年的总收入为x万元,总支出为y万元,则有:
总收入/万元 总支出/万元 利润/万元
去年
今年
x
y
200
(1+20%)x
(1-10%)y
780
3:正确书写解题过程
解:设去年的总收入为x万元,总支出为y万元,则今年的总收入为(1+20%)x万元,今年的总支出为(1-10%)y万元.
根据题意,得
解得
答:去年的总收入为2 000万元,总支出为1 800万元.
x-y=200,
(1+20%) x - (1 - 10%) y=780.
x=2000, y=1800.
应用举例
例1 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质,若病人每餐需要35单位蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰好满足病人的需要
解:设每餐需甲原料x g、乙原料y g,则有
甲原料x g 乙原料y g 所配制的营养品
其中所含蛋白质 0.5x 0.7y 35
其中所含铁质 x 0.4y 40
根据上表,可以列出方程组 ,
解得 .
所以每餐需甲原料28g、乙原料30g.
0.5x+0.7y=35
x+0.4y=40
x=28
y=30
例2 我区某学校原计划向内蒙古察右旗地区的学生捐赠3 500册图书,实际共捐赠了4 125册,其中初中学生捐赠了原计划的120%,高中学生捐赠了原计划的115%,初中学生和高中学生各比原计划多捐赠图书多少册?
解:设原计划初中学生捐x册,高中学生捐y册,填写下表.
初中学生捐的数量 高中学生捐的数量 合计
计划
实际
x
y
3 500
120%x
115%y
4 125
根据上表列方程组,得
解得
初中学生比原计划多捐的册数是2 000×(120%-1)=400(册),
高中学生比原计划多捐的册数是1 500×(115%-1)=225(册),
答:初中学生和高中学生各比原计划多捐赠图书400册和225册.
x+y=3500,
120%x+115 % y=4125.
x=2000, y=1500.
课堂小结
列方程组解决实际问题
增长率、利润问题
利用图表分析等量关系
随堂练习
1.某市现有人口45万,计划一年后城镇人口增加0.7%,农村人口增加1.2%,这样,全市人口将增加1%,求这个市现在的城镇人口与农村人口.设现在城镇人口有x万,农村人口有y万,则下列方程组中正确的是( )
B
2.将浓度为30%的酒精与浓度为60%的酒精混合,制成了浓度为50%的酒精30 kg.设浓度为30%的酒精需要x kg,浓度为60%的酒精需要y kg,则列出的方程组为
—————————————.
x+y=30,
30%x+60 % y=50 %×30
3.今年“五一”小长假期间,某市外来与外出旅游的总人数为226万人,分别比去年同期增长30%和20%,去年同期外来旅游比外出旅游的人数多20万人.求该市今年外来和外出旅游的人数.
解:设去年外来旅游的人数为x万人,外出旅游的人数为y万人.
根据题意,得 解得
所以(1+30%)x=(1+30%)×100=130,
(1+20%)y=(1+20%)×80=96.
答:该市今年外来和外出旅游的人数分别是130万人和96万人.
x-y=20,
(1+30%)x+(1+20%) y=226.
x=100, y=80.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
