6.3 从统计图分析数据的集中趋势 课件(共19张PPT)
文档属性
| 名称 | 6.3 从统计图分析数据的集中趋势 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 639.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 17:58:32 | ||
图片预览


文档简介
(共19张PPT)
第六章 数据的分析
3 从统计图分析数据的集中趋势
北师版 八年级 数学(上)
导入新课
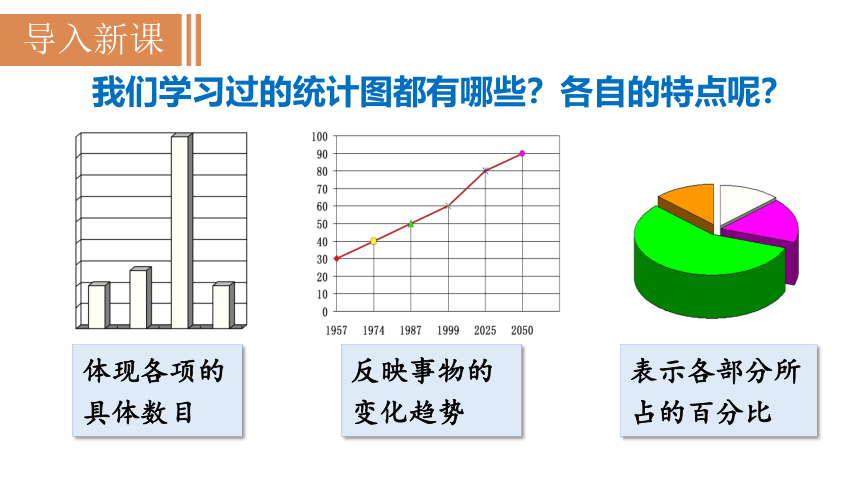
体现各项的具体数目
反映事物的变化趋势
表示各部分所占的百分比
我们学习过的统计图都有哪些?各自的特点呢?
探究新知
探究
为了检查面包的质量是否达标,随机抽取了同种规格的面包10个,这10个面包的质量如下图所示:
99.8克
100克
100克
(1)这10个面包质量的中位数是 众数是 .
(2)估算平均质量是 算一算验证你的估计。
探究新知
探究
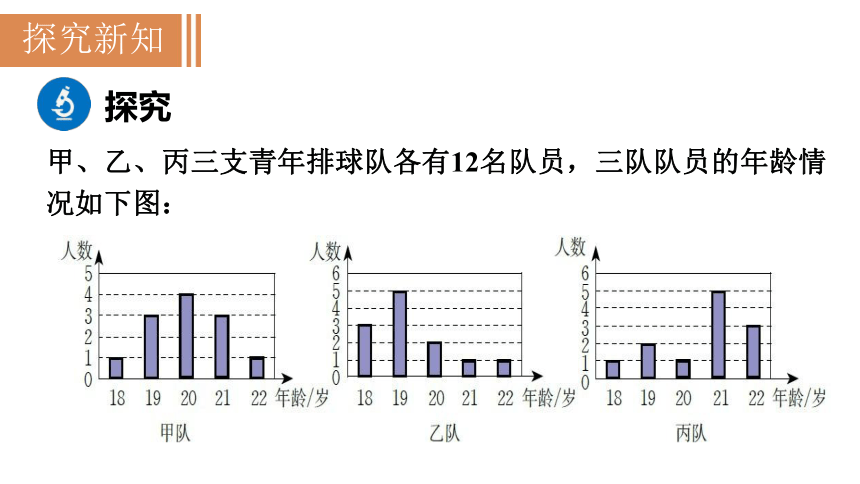
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
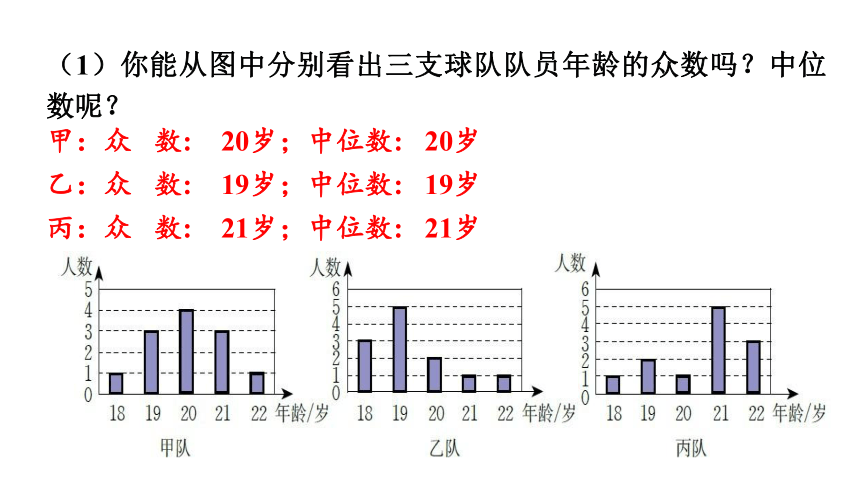
(1)你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?
甲:众 数: 20岁;中位数: 20岁
乙:众 数: 19岁;中位数: 19岁
丙:众 数: 21岁;中位数: 21岁
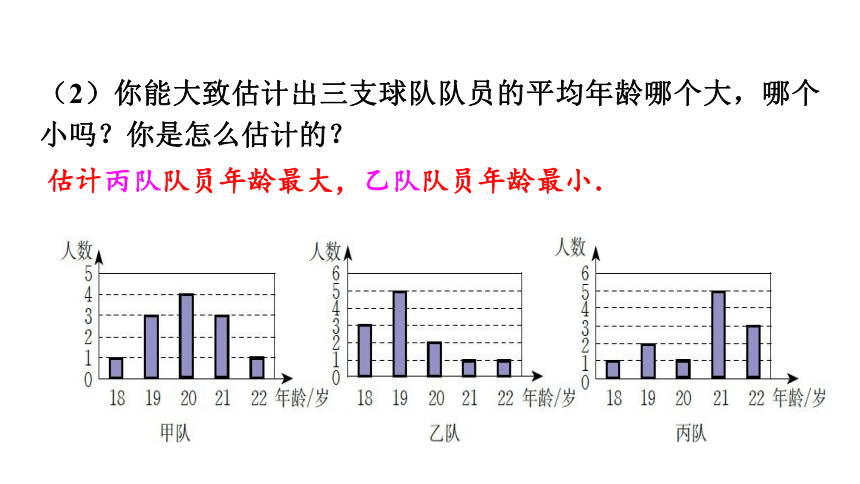
(2)你能大致估计出三支球队队员的平均年龄哪个大,哪个小吗?你是怎么估计的?
估计丙队队员年龄最大,乙队队员年龄最小.
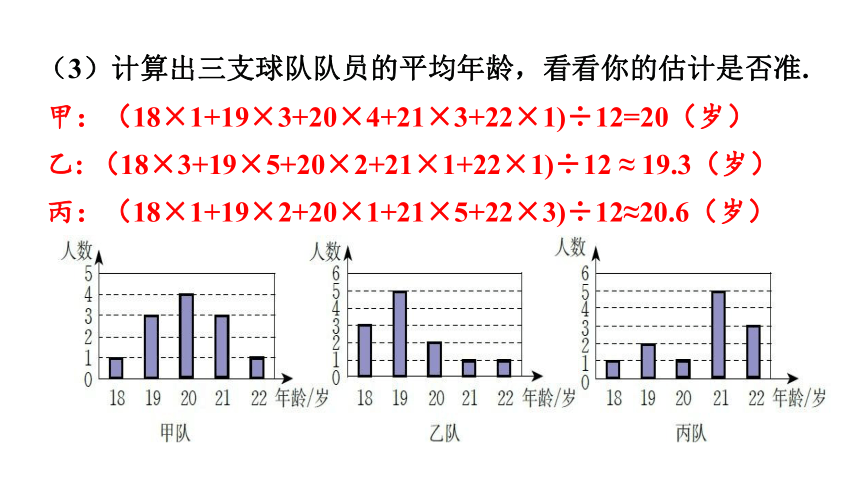
(3)计算出三支球队队员的平均年龄,看看你的估计是否准.
甲:(18×1+19×3+20×4+21×3+22×1)÷12=20(岁)
乙: (18×3+19×5+20×2+21×1+22×1)÷12 ≈ 19.3(岁)
丙:(18×1+19×2+20×1+21×5+22×3)÷12≈20.6(岁)
探究新知
探究
小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示:
(1)在这名同学中,本学期计划购买课外书的花费的众数是多少?
(2)计算这20名同学计划购买课外书的平均花费。
(1)众数是50元。
(2)
平均花费是57元
折线统计图能够表示数据的变化趋势,利用它可以比较容易看出众数;
条形统计图能清楚表示出数量的多少,可以容易看出众数、中位数;
扇形统计图能看出部分在总体所占的百分比,可以容易看出众数、中位数.三种统计图都可以求平均数.
归纳总结
应用举例
例1 某地连续统计了10天日最高气温,绘制成如图扇形统计图.
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值.
解:(1)根据扇形统计图,35℃占的比例最大,所以日平均气温的众数是35℃ 。
(2)这10天日最高气温的平均值是:
32×10%+33×20%+34×20%+35×30%+36×20%=34.3℃
例2 为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题.
(1)本次接受随机抽样调查的学生人数为________,图①中m的值为________;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
40
15
(2)∵在这组样本数据中,35出现了12次,出现次数最多,∴这组样本的众数为35;将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都为36,
∴中位数为 =36;
36+36
2
(3)∵在40名学生中,鞋号为35的学生人数比例为30%,∴由样本数据估计学校各年级中学生鞋号为35的人数比例约为30%,则计划购买200双运动鞋,35号的运动鞋数量为200×30%=60(双).
课堂小结
从统计图分析数据的集中趋势
折线统计图
条形统计图
扇形统计图
随堂练习
根据下列统计图,写出相应分数的平均数、众数和中位数.
解:(1)平均数: =3(分).
中位数和众数都是3;
(2)平均数:1×3%+2×4%+3×51%+4×32%+5×10%=3.42(分).中位数和众数都是3分.
第六章 数据的分析
3 从统计图分析数据的集中趋势
北师版 八年级 数学(上)
导入新课
体现各项的具体数目
反映事物的变化趋势
表示各部分所占的百分比
我们学习过的统计图都有哪些?各自的特点呢?
探究新知
探究
为了检查面包的质量是否达标,随机抽取了同种规格的面包10个,这10个面包的质量如下图所示:
99.8克
100克
100克
(1)这10个面包质量的中位数是 众数是 .
(2)估算平均质量是 算一算验证你的估计。
探究新知
探究
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
(1)你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?
甲:众 数: 20岁;中位数: 20岁
乙:众 数: 19岁;中位数: 19岁
丙:众 数: 21岁;中位数: 21岁
(2)你能大致估计出三支球队队员的平均年龄哪个大,哪个小吗?你是怎么估计的?
估计丙队队员年龄最大,乙队队员年龄最小.
(3)计算出三支球队队员的平均年龄,看看你的估计是否准.
甲:(18×1+19×3+20×4+21×3+22×1)÷12=20(岁)
乙: (18×3+19×5+20×2+21×1+22×1)÷12 ≈ 19.3(岁)
丙:(18×1+19×2+20×1+21×5+22×3)÷12≈20.6(岁)
探究新知
探究
小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示:
(1)在这名同学中,本学期计划购买课外书的花费的众数是多少?
(2)计算这20名同学计划购买课外书的平均花费。
(1)众数是50元。
(2)
平均花费是57元
折线统计图能够表示数据的变化趋势,利用它可以比较容易看出众数;
条形统计图能清楚表示出数量的多少,可以容易看出众数、中位数;
扇形统计图能看出部分在总体所占的百分比,可以容易看出众数、中位数.三种统计图都可以求平均数.
归纳总结
应用举例
例1 某地连续统计了10天日最高气温,绘制成如图扇形统计图.
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值.
解:(1)根据扇形统计图,35℃占的比例最大,所以日平均气温的众数是35℃ 。
(2)这10天日最高气温的平均值是:
32×10%+33×20%+34×20%+35×30%+36×20%=34.3℃
例2 为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题.
(1)本次接受随机抽样调查的学生人数为________,图①中m的值为________;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
40
15
(2)∵在这组样本数据中,35出现了12次,出现次数最多,∴这组样本的众数为35;将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都为36,
∴中位数为 =36;
36+36
2
(3)∵在40名学生中,鞋号为35的学生人数比例为30%,∴由样本数据估计学校各年级中学生鞋号为35的人数比例约为30%,则计划购买200双运动鞋,35号的运动鞋数量为200×30%=60(双).
课堂小结
从统计图分析数据的集中趋势
折线统计图
条形统计图
扇形统计图
随堂练习
根据下列统计图,写出相应分数的平均数、众数和中位数.
解:(1)平均数: =3(分).
中位数和众数都是3;
(2)平均数:1×3%+2×4%+3×51%+4×32%+5×10%=3.42(分).中位数和众数都是3分.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
