2022-2023学年高一上学期数学人教A版必修第一册 第七节 对数与对数函数题型训练讲义 (Word含答案)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版必修第一册 第七节 对数与对数函数题型训练讲义 (Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 409.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 00:00:00 | ||
图片预览


文档简介
第七节 对数与对数函数
知识清单
一.对数
1.对数的概念
一般地,如果,那么叫做以为底的对数,记作,
其中叫做对数的底数,叫做真数.
2.对数与指数的关系
当时,,负数和0没有对数.
3.两种特殊的对数
(1)通常,我们将以10为底的对数叫做常用对数,并把记作.
(2)以无理数为底的对数叫做自然对数,并把记作.
4.对数的运算
(1)恒等式()
① ② ③
(2)对数的运算性质()
①
②
③
(3)对数换底公式()
(4)常用推论
① ()
②()
二.对数函数
1.对数函数的定义
一般地,函数叫做对数函数,其中是自变量,定义域是.
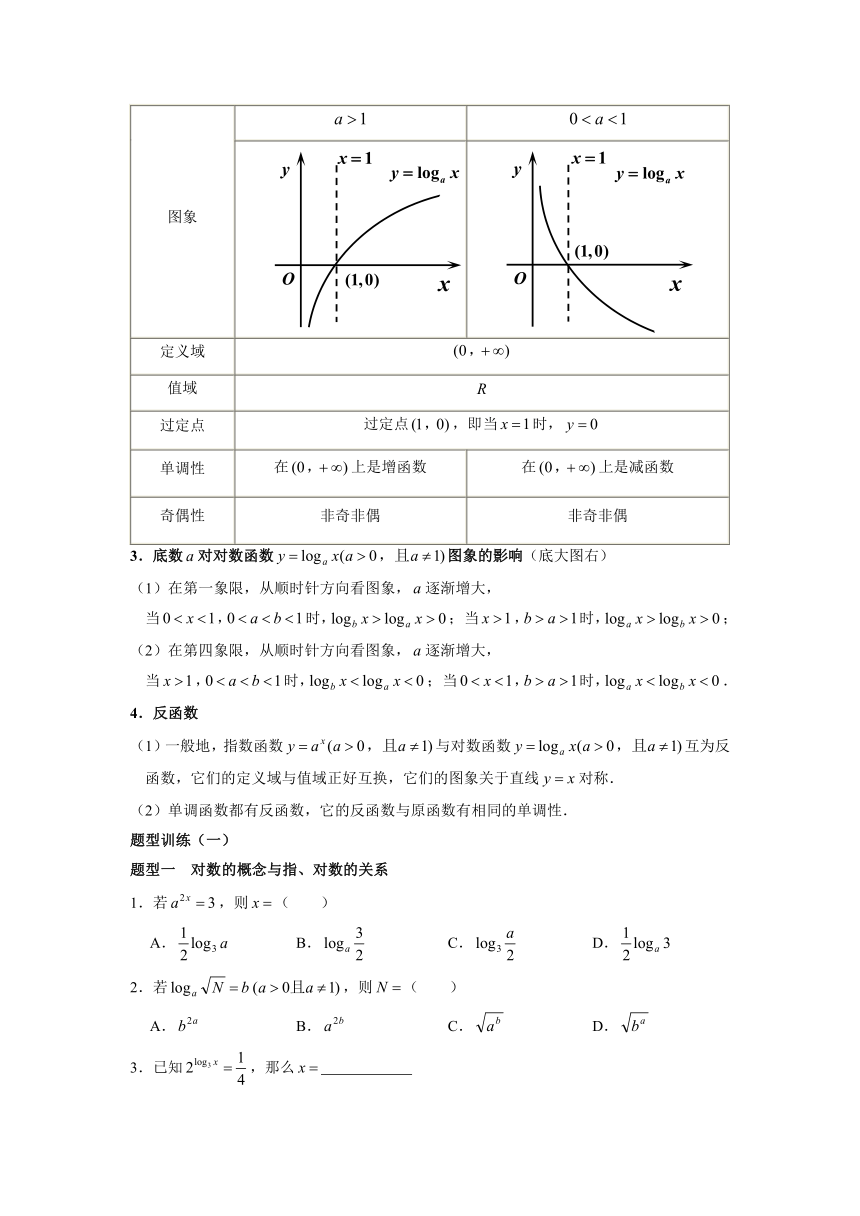
2.对数函数的图象及性质
函数
图象
(
0
1
) (
0
1
)
定义域
值域
过定点 过定点,即当时,
单调性 在上是增函数 在上是减函数
奇偶性 非奇非偶 非奇非偶
3.底数对对数函数图象的影响(底大图右)
(1)在第一象限,从顺时针方向看图象,逐渐增大,
当,时,; 当,时,;
(2)在第四象限,从顺时针方向看图象,逐渐增大,
当,时,; 当,时,.
4.反函数
(1)一般地,指数函数与对数函数互为反函数,它们的定义域与值域正好互换,它们的图象关于直线对称.
(2)单调函数都有反函数,它的反函数与原函数有相同的单调性.
题型训练(一)
题型一 对数的概念与指、对数的关系
1.若,则( )
A. B. C. D.
2.若,则( )
A. B. C. D.
3.已知,那么
4.已知,那么
题型二 对数的运算性质与换底公式
5.若,则( )
A. B. C.1 D.
6.设,,则( )
A. B. C. D.
7.(1) ,(2)
8.(1) ,(2)
题型三 对数运算综合
9.已知,,,,则下列等式一定成立的是( )
A. B. C. D.
10.已知,那么用表示是( )
A. B. C. D.
11.已知,则
12.已知,若,则
题型训练(二)
题型一 对数函数的定义域
1.函数的定义域是( )
A. B. C. D.
2.函数的定义域为
题型二 对数函数的值域问题
3.已知函数区间上恒有,则实数的取值范围是( )
A. B. C. D.
4.函数的值域为
5.函数在区间上的最大值为 ,最小值为
6.已知函数,若的定义域为,则实数的取值范围是 ,
若的值域为,则实数的取值范围是
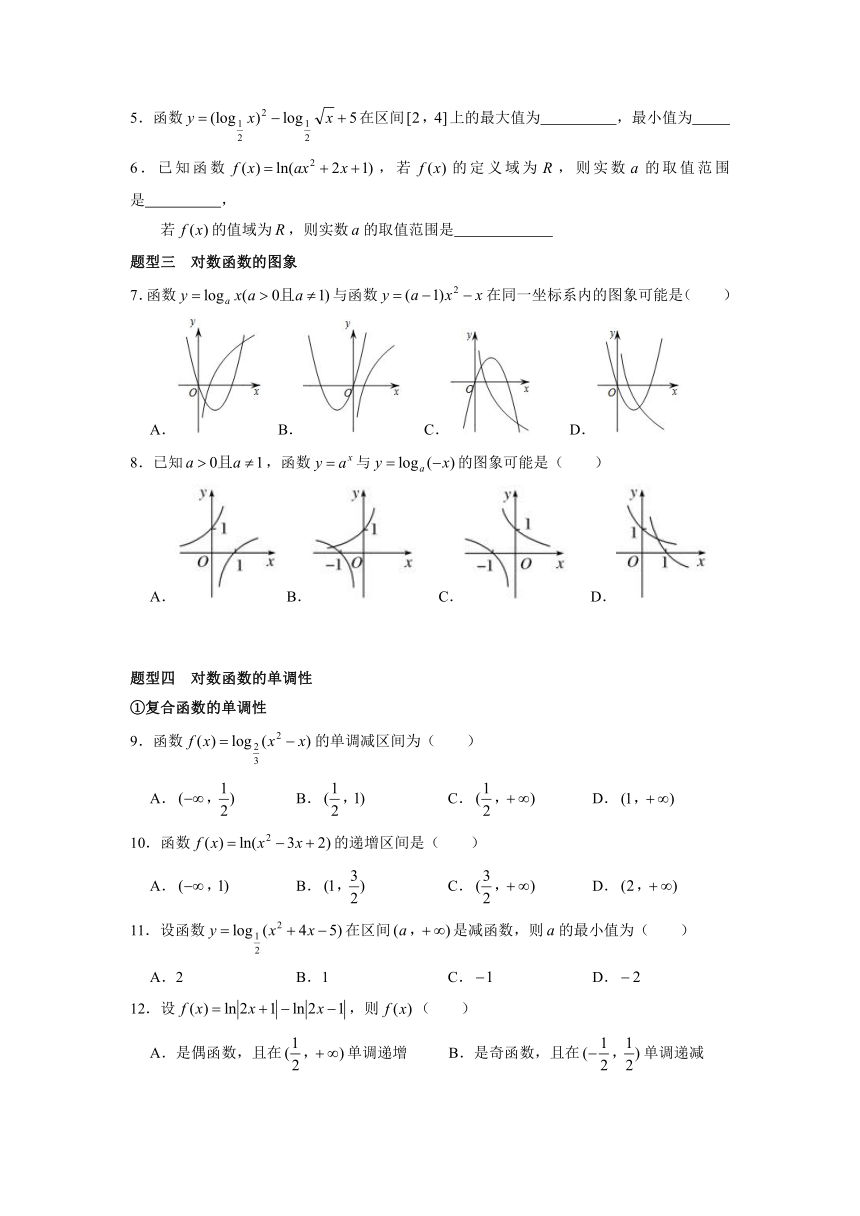
题型三 对数函数的图象
7.函数与函数在同一坐标系内的图象可能是( )
A. B. C. D.
8.已知,函数与的图象可能是( )
A. B. C. D.
题型四 对数函数的单调性
①复合函数的单调性
9.函数的单调减区间为( )
A. B. C. D.
10.函数的递增区间是( )
A. B. C. D.
11.设函数在区间是减函数,则的最小值为( )
A.2 B.1 C. D.
12.设,则( )
A.是偶函数,且在单调递增 B.是奇函数,且在单调递减
C.是偶函数,且在单调递增 D.是奇函数,且在单调递减
②单调性的应用
13.设为正实数,则“”是“”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
14.不等式的解集为
15.不等式的解集为
16.已知,则实数的取值范围是
题型五 对数函数相关的奇偶性问题
17.已知函数,若,则
18.已知函数是奇函数.
(1)求的值;
(2)判定在上的单调性,并加以证明.
题型六 对数式比较大小
①化为同底数
19.设,则的大小关系是( )
A. B. C. D.
20.已知,则的大小关系为( )
A. B. C. D.
②化为同真数
21.设,则( )
A. B. C. D.
22.若,则( )
A. B. C. D.
③找中间值
23.已知,则( )
A. B. C. D.
24.设,则三者大小关系为( )
A. B. C. D.
25.已知,则下列判断正确的是( )
A. B. C. D.
26.设,则( )
A. B. C. D.
题型七 反函数
27.若函数的反函数的图象过点,则函数的图象必过点( )
A. B. C. D.
28.若函数与的图象关于对称,且,则( )
A.3 B.4 C.6 D.20
综合训练
1.设,则( )
A. B. C. D.
2.设,,则( )
A. B. C. D.
3.已知,则( )
A.25 B.5 C. D.
4.若,则( )
A. B. C. D.
5.已知,则的大小关系为( )
A. B. C. D.
6.已知函数的定义域为,则函数的定义域为( )
A. B. C. D.
7.已知,则的大小关系为( )
A. B. C. D.
8.已知函数在上单调递增,则的取值范围是( )
A. B. C. D.
9.设是定义域为的偶函数,且在单调递减,则( )
A. B.
C. D.
10.已知.设,则( )
A. B. C. D.
11.设,则( )
A. B. C. D.
12.已知为正数,且,则( )
A. B. C. D.
13.函数的图象恒过定点
14.设函数是定义在上的奇函数,且,则
15.已知,则的大小关系为
16.已知函数,若函数在上单调递减,
则实数的取值范围是
17.已知.
(1)若的定义域为,求实数的取值范围;
(2)若函数在区间上是单调递增的,求实数的取值范围.
18.已知是偶函数.
(1)求的值;
(2)判断在上的单调性;
(3)若函数,是否存在实数使得有最小值0?
若存在,求出的值;若不存在,请说明理由.
第七节 对数与对数函数
题型训练(一)
题型一 对数的概念与指、对数的关系
1-2 D,B 3. 4.8
题型二 对数的运算性质与换底公式
5.C 6.D
7.(1) (2)3
8.(1)10 (2)4
题型三 对数运算综合
9-10 B,A 11. 12.
题型训练(二)
题型一 对数函数的定义域
1.A 2.
题型二 对数函数的值域问题
3.D 4. 5.10, 6.,
题型三 对数函数的图象
7-8 A,B
题型四 对数函数的单调性
9-13 D,D,B,D,A 14. 15. 16.
题型五 对数函数相关的奇偶性问题
17. 18.(1) (2)在上的单调递减,证明略
题型六 对数式比较大小
19-22 B,A,D,D 23-26 B,D,C,A
题型七 反函数
27-28 C,A
综合训练
1-5 B,C,C,B,A 6-10 D,D,D,C,A 11-12 B,D
13. 14. 15. 16.
17.(1) (2)
18.(1) (2)在上的单调递增 (3)
知识清单
一.对数
1.对数的概念
一般地,如果,那么叫做以为底的对数,记作,
其中叫做对数的底数,叫做真数.
2.对数与指数的关系
当时,,负数和0没有对数.
3.两种特殊的对数
(1)通常,我们将以10为底的对数叫做常用对数,并把记作.
(2)以无理数为底的对数叫做自然对数,并把记作.
4.对数的运算
(1)恒等式()
① ② ③
(2)对数的运算性质()
①
②
③
(3)对数换底公式()
(4)常用推论
① ()
②()
二.对数函数
1.对数函数的定义
一般地,函数叫做对数函数,其中是自变量,定义域是.
2.对数函数的图象及性质
函数
图象
(
0
1
) (
0
1
)
定义域
值域
过定点 过定点,即当时,
单调性 在上是增函数 在上是减函数
奇偶性 非奇非偶 非奇非偶
3.底数对对数函数图象的影响(底大图右)
(1)在第一象限,从顺时针方向看图象,逐渐增大,
当,时,; 当,时,;
(2)在第四象限,从顺时针方向看图象,逐渐增大,
当,时,; 当,时,.
4.反函数
(1)一般地,指数函数与对数函数互为反函数,它们的定义域与值域正好互换,它们的图象关于直线对称.
(2)单调函数都有反函数,它的反函数与原函数有相同的单调性.
题型训练(一)
题型一 对数的概念与指、对数的关系
1.若,则( )
A. B. C. D.
2.若,则( )
A. B. C. D.
3.已知,那么
4.已知,那么
题型二 对数的运算性质与换底公式
5.若,则( )
A. B. C.1 D.
6.设,,则( )
A. B. C. D.
7.(1) ,(2)
8.(1) ,(2)
题型三 对数运算综合
9.已知,,,,则下列等式一定成立的是( )
A. B. C. D.
10.已知,那么用表示是( )
A. B. C. D.
11.已知,则
12.已知,若,则
题型训练(二)
题型一 对数函数的定义域
1.函数的定义域是( )
A. B. C. D.
2.函数的定义域为
题型二 对数函数的值域问题
3.已知函数区间上恒有,则实数的取值范围是( )
A. B. C. D.
4.函数的值域为
5.函数在区间上的最大值为 ,最小值为
6.已知函数,若的定义域为,则实数的取值范围是 ,
若的值域为,则实数的取值范围是
题型三 对数函数的图象
7.函数与函数在同一坐标系内的图象可能是( )
A. B. C. D.
8.已知,函数与的图象可能是( )
A. B. C. D.
题型四 对数函数的单调性
①复合函数的单调性
9.函数的单调减区间为( )
A. B. C. D.
10.函数的递增区间是( )
A. B. C. D.
11.设函数在区间是减函数,则的最小值为( )
A.2 B.1 C. D.
12.设,则( )
A.是偶函数,且在单调递增 B.是奇函数,且在单调递减
C.是偶函数,且在单调递增 D.是奇函数,且在单调递减
②单调性的应用
13.设为正实数,则“”是“”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
14.不等式的解集为
15.不等式的解集为
16.已知,则实数的取值范围是
题型五 对数函数相关的奇偶性问题
17.已知函数,若,则
18.已知函数是奇函数.
(1)求的值;
(2)判定在上的单调性,并加以证明.
题型六 对数式比较大小
①化为同底数
19.设,则的大小关系是( )
A. B. C. D.
20.已知,则的大小关系为( )
A. B. C. D.
②化为同真数
21.设,则( )
A. B. C. D.
22.若,则( )
A. B. C. D.
③找中间值
23.已知,则( )
A. B. C. D.
24.设,则三者大小关系为( )
A. B. C. D.
25.已知,则下列判断正确的是( )
A. B. C. D.
26.设,则( )
A. B. C. D.
题型七 反函数
27.若函数的反函数的图象过点,则函数的图象必过点( )
A. B. C. D.
28.若函数与的图象关于对称,且,则( )
A.3 B.4 C.6 D.20
综合训练
1.设,则( )
A. B. C. D.
2.设,,则( )
A. B. C. D.
3.已知,则( )
A.25 B.5 C. D.
4.若,则( )
A. B. C. D.
5.已知,则的大小关系为( )
A. B. C. D.
6.已知函数的定义域为,则函数的定义域为( )
A. B. C. D.
7.已知,则的大小关系为( )
A. B. C. D.
8.已知函数在上单调递增,则的取值范围是( )
A. B. C. D.
9.设是定义域为的偶函数,且在单调递减,则( )
A. B.
C. D.
10.已知.设,则( )
A. B. C. D.
11.设,则( )
A. B. C. D.
12.已知为正数,且,则( )
A. B. C. D.
13.函数的图象恒过定点
14.设函数是定义在上的奇函数,且,则
15.已知,则的大小关系为
16.已知函数,若函数在上单调递减,
则实数的取值范围是
17.已知.
(1)若的定义域为,求实数的取值范围;
(2)若函数在区间上是单调递增的,求实数的取值范围.
18.已知是偶函数.
(1)求的值;
(2)判断在上的单调性;
(3)若函数,是否存在实数使得有最小值0?
若存在,求出的值;若不存在,请说明理由.
第七节 对数与对数函数
题型训练(一)
题型一 对数的概念与指、对数的关系
1-2 D,B 3. 4.8
题型二 对数的运算性质与换底公式
5.C 6.D
7.(1) (2)3
8.(1)10 (2)4
题型三 对数运算综合
9-10 B,A 11. 12.
题型训练(二)
题型一 对数函数的定义域
1.A 2.
题型二 对数函数的值域问题
3.D 4. 5.10, 6.,
题型三 对数函数的图象
7-8 A,B
题型四 对数函数的单调性
9-13 D,D,B,D,A 14. 15. 16.
题型五 对数函数相关的奇偶性问题
17. 18.(1) (2)在上的单调递减,证明略
题型六 对数式比较大小
19-22 B,A,D,D 23-26 B,D,C,A
题型七 反函数
27-28 C,A
综合训练
1-5 B,C,C,B,A 6-10 D,D,D,C,A 11-12 B,D
13. 14. 15. 16.
17.(1) (2)
18.(1) (2)在上的单调递增 (3)
