1.1 探索勾股定理(2)

课 题：第一章 第一节 探索勾股定理(2)
课 型：新授课
授课时间：2013年9月3日 星期二 第1、2节课
教学目标：
1.经历勾股定理的验证过程，体会数形结合的思想和从特殊到一般的思想.
2. 掌握勾股定理及其验证，并能应用勾股定理解决一些实际问题.
教学重点：
用面积法验证勾股定理，应用勾股定理解决简单的实际问题.
教学难点：
验证勾股定理.
教法与学法指导：
学生上节课又已经通过测量和数格子的方法，对具体的直角三角形探索并发现了勾股定理，但没有对一般的直角三角形进行验证. 本节课是在上节课已探索得到勾股定理之后的内容，通过拼图验证勾股定理并体会其中数形结合的思想；应用勾股定理解决一些实际问题.本节课我采用的是“自主探究、当堂评价”的方法，通过拼图的方法，师生共同构证明出来勾股定理，应用勾股定理解决一些实际问题，提升能力．
课前准备：生∶四个全等的直角三角形图片 师∶制作课件
一、回顾与复习
师：上节课我们已经通过探索得到了勾股定理，请问勾股定理的内容是什么？
生：直角三角形两直角边的平方和等于斜边的平方.如果用a、b和c分别表示直角三角形的两直角边和斜边，那么a 2＋b2=c 2
师：上节课我们仅仅是通过测量和数格子，对具体的直角三角形探索发现了勾股定理，对一般的直角三角形，勾股定理是否成立呢？
生：成立.
活动目的：复习勾股定理内容；回顾上节课探索过程，强调仍需对一般的直角三角形进行验证，培养学生严谨的科学态度.
二、拼图验证
师：这需要进一步验证，如何验证勾股定理呢？
(只有预习的同学会一些,因此提示：利用准备好的四个全等的直角三角形图片,拼出一个正方形)
（教师可参与到学生的讨论中，发现同学们不足的地方，给予提示和指导）.
师：（利用投影机展示同学们拼的好一些的正方形）
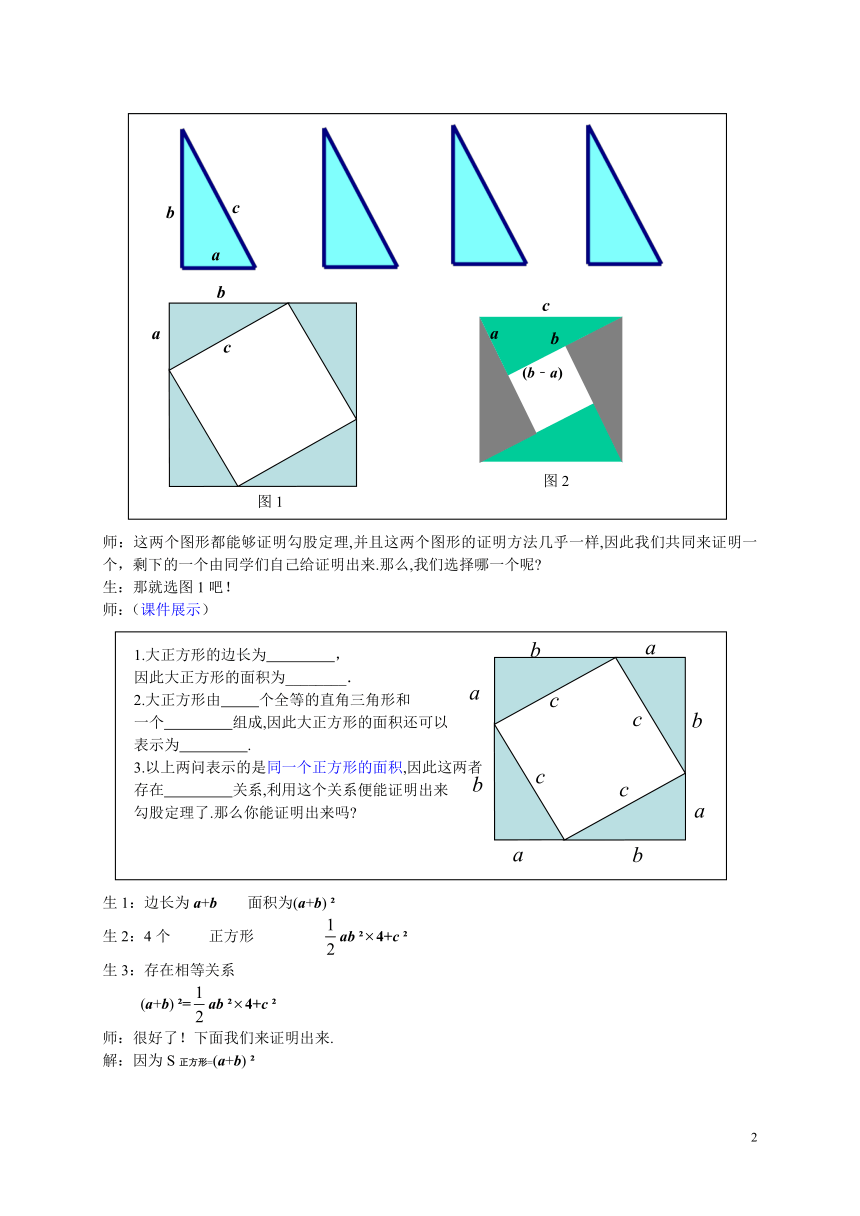
师：这两个图形都能够证明勾股定理,并且这两个图形的证明方法几乎一样,因此我们共同来证明一个，剩下的一个由同学们自己给证明出来.那么,我们选择哪一个呢?
生：那就选图1吧！
师：（课件展示）
1.大正方形的边长为 ，
因此大正方形的面积为________．
2.大正方形由 个全等的直角三角形和
一个 组成,因此大正方形的面积还可以
表示为 .
3.以上两问表示的是同一个正方形的面积,因此这两者
存在 关系,利用这个关系便能证明出来
勾股定理了.那么你能证明出来吗?
生1：边长为a+b 面积为(a+b) 2
生2：4个 正方形 ab 24+c 2
生3：存在相等关系
(a+b) 2=ab 24+c 2
师：很好了！下面我们来证明出来.
解：因为S正方形=(a+b) 2
S正方形=ab 24+c 2
所以(a+b) 2=ab 24+c 2
a 2+2ab+b 2=2ab+ c 2
a 2+b2= c 2
活动目的：为了让学生在活动中体会图形的构成，既为勾股定理的验证作铺垫，同时也培养学生的动手、创新能力.
师：对于图2的证明方法几乎和图1的证明方法一样，也是都表示正方形的面积，寻找相等关系，便能证明出勾股定理了.下面自己做出来,然后小组选出代表来回答.
(师巡视,多注意有困难的学生,给出适当的提示和帮助)
生2：因为S正方形=c 2
S正方形=ab 24+(b-a) 2
所以c 2=ab 24+(b-a) 2 （课件展示图形）
c 2= 2ab+ b 2-2ab+a 2
c 2= a 2+b2
即：a 2+b2= c 2
活动目的：让学生利用另一个拼图独立验证勾股定理的目的是让学生再次体会数形结合的思想并加以运用,体会成功的快乐
三、追溯历史
师：这位同学证明的太好了！其实勾股定理的证明方法有400多种,下面我们就介绍几种证明方法
.
1.方法一：三国时期吴国数学家赵爽在为《周髀算经》作注解时，创制了一幅“勾股圆方图”， 也称为“弦图”，这是我国对勾股定理最早的证明.


2002年世界数学家大会在北京召开，这届大会会标的中央图案正是经过艺术处理的“弦图”，标志着中国古代数学成就.
2.美国总统证法
在1876年一个周末的傍晚，在美国首都华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景……他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨．由于好奇心驱使他循声向两个小孩走去，想搞清楚两个小孩到底在干什么．只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形……
于是这位中年人不再散步，立即回家，潜心探讨小男孩给他留下
的难题.他经过反复的思考与演算，终于弄清楚了其中的道理，并给
出了简洁的证明方法. 1876年4月1日，他在《新英格兰教育日志》上发表了他对勾股定理的这一证法.
师：对于这个题目的证明方法几乎和图1和图2的证明方法差不多，也是都表示梯形的面积，寻找相等关系，便能证明出勾股定理了.我们课下习题中也有.
3.方法三：据传是当年毕达哥拉斯发现勾股定理时做出的证明.
将4个全等的直角三角形拼成边长为(a＋b)的正方形ABCD，使中间留下边长c的一个正方形洞．画出正方形ABCD．移动三角形至图2所示的位置中，于是留下了边长分别为a与b的两个正方形洞．则图1和图2中的白色部分面积必定相等，所以c2=a2+b2

4.方法4：我国的“青朱出入图”, 清楚地发现图中:小正方形与较大正方形的面积和与最大正方形的面积之间的等量关系,从而不用运算,单靠移动几块图形就直观地证出了勾股定理,真是“无字的证明”.


活动目的：介绍与勾股定理有关的历史，学生加强了对数学史的了解，培养学习数学的兴趣；既让学生得到充分的锻炼，同时也活跃了课堂气氛.
四 、例题讲解 初步应用
例题：我方侦察员小王在距离东西向公路400m处侦察，发现一辆
地方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他
相距400m,10s后，汽车与他相距500m.
你能帮小王计算地方汽车的速度吗？
师：解：有勾股定理得ＡＢ2＝BC 2 +AC 2
即：5002= BC 2+400 2
所以BC=300
1h行驶了300×6×60=108000﹙m﹚
所以它的行驶速度为108km／h
活动目的：初步运用勾股定理解决实际问题，培养学生应用数学的意识和能力；体会勾股定理的应用价值,把实际问题转化为数学问题并顺利解决.
五、延伸拓展，能力提升
1.议一议:观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2
2.一个直角三角形的斜边为20cm?,且两直角边长度比为3:4，求两直角边的长.
生1：这两个都不满足勾股定理.
生2： =5
20 5=4
3×4=12﹙cm﹚
4×4=16﹙cm﹚
活动目的：学生通过数格子的方法可以得出：如果一个三角形不是直角三角形，那么它的三边a,b,c不满足a2+b2=c2.通过这个结论，学生将对直角三角形三边的关系有进一步的认识，并为后续直角三角形的判别打下基础.
六、达标检测
1．若△ABC中，∠C=90°，（1）若a=5，b=12，则c= ；（2）若a=6，c=10，则b= ；（3）若a∶b=3∶4，c=10，则a= ，b= .
2．某农舍的大门是一个木制的矩形栅栏，它的高为2 m，宽为1.5 m，现需要在相对的顶点间用一块木棒加固，木板的长为 .
3．直角三角形两直角边长分别为5 cm，12 cm，则斜边上的高为 .
4．等腰三角形的腰长为13 cm，底边长为10 cm，则面积为（ ）.
A．30 cm2 B．130 cm2 C．120 cm2 D．60 cm2
七、提高检测
5．一棵9 m高的树被风折断，树顶落在离树根3 m之处，若要查看断痕，要从树底开始爬多高？
八、知识拓展（学有余力的同学课下完成）
6．折叠长方形ABCD的一边AD，使点D落在BC边的F点处，
若AB=8 cm，BC=10 cm，求EC的长.
参考答案：
1．（1）13；（2）8；（3）6，8．
2．2.5m．
3．cm．
4．D．
5．4m．
7．3 cm．
活动目的：设计分层训练，既满足了不同学生的需求，同时也便于老师及时地了解学生的情况,及时给出指导与评价.
九、回顾反思 提炼升华
师：通过这节课的学习，你有什么样的收获？
生1：会证明勾股定理,了解不少方法.
生2：数形结合的思想方法
生3：会背诵常见的勾股数利于做难一些的题目. ……
活动目的：归纳出本节课的知识要点，数形结合的思想方法；了解学生对本节课的感受并进行总结；培养学生的归纳概括能力.
九、课后练习
必做题：　　课本第6页习题1.2第 1，2题.
选做题：　　课本第7页习题1.2第3题．
板书设计：
1.1探索勾股定理(2)
勾股定理
拼图验证
追溯历史
例题
5. 达标检测
6.板书区
教学反思：
勾股定理作为“千古第一定理”其魅力在于其历史价值和应用价值，因此我也注意充分挖掘了其内涵.让学生事先进行准备直角三角形图片，再在课堂上进行展示，自己拼出正方形,证明勾股定理,这极大地调动了学生，加深了对勾股定理文化的理解．勾股定理的验证既是本节课的重点，也是本节课的难点，为了突破这一难点，设计了拼图活动，先让学生从形上感知，再层层设问，从面积（数）入手，师生共同探究得到方法1，最后由学生独立探究得到方法2．这样学生较容易地突破了本节课的难点．利用几何画板展示“青朱出入图”,又展示了几种勾股定理的证明方法,学生印象很深.
改进方面：多关注学困生,多指导,多提示会效果更好一些.