2022-2023学年北师大版八年级数学上册1.1探索勾股定理 周末综合作业题 (Word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册1.1探索勾股定理 周末综合作业题 (Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 287.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-03 00:00:00 | ||
图片预览

文档简介
2022-2023学年北师大版八年级数学上册《1.1探索勾股定理》周末综合作业题(附答案)
一.选择题(共8小题,满分40分)
1.直角三角形的边长分别为a,b,c,且∠C=90°,若a2=9,b2=16,那么c2的值是( )
A.5 B.7 C.25 D.49
2.如图,阴影部分是一个长方形,则长方形的面积是( )
A.4cm2 B.5cm2 C.6cm2 D.12cm2
3.如图,在△ABC中,∠B=90°,AB=2、BC=4,四边形ADEC是正方形,则正方形ADEC的面积是( )
A.8 B.16 C.20 D.25
4.如图,在Rt△ABC中,∠ACB=90°.若AC=5,则正方形ABDE和正方形CBGF的面积差为( )
A.10 B.15 C.20 D.25
5.在Rt△ABC中,∠C=90°,a、b、c为三边,则下列关系不正确的是( )
A.a2+b2=c2 B.a+b>c C.c﹣a>b D.c﹣b<a
6.△ABC中,AB=20,AC=13,高AD=12,则△ABC的面积为( )
A.66 B.126 C.54或44 D.126或66
7.如图,正方形ABCD的面积为15,Rt△BCE的斜边CE的长为8,则BE的长为( )
A.17 B.10 C.6 D.7
8.如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼接成的大正方形,若直角三角形的两条直角边长分别为a,b(a>b),大正方形的面积为S1,小正方形的面积为S2,则用含S1,S 的代数式表示(a+b)2正确的是( )
A.S1 B.S2 C.2S1﹣S2 D.2S2﹣S1
二.填空题(共8小题,满分40分)
9.在Rt△ABC中,斜边BC=10,则BC2+AB2+AC2= .
10.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为 .
11.如图,点C是线段AB上一点,以AC、BC为边向两边作正方形ACDE和BCFG,已知AB=10,两正方形的面积和S1+S2=60,则图中阴影部分的面积为 .
12.如图,已知△ABC中,∠C=90°,AB=10,BC=6,若点D为AB边上任意一点,则线段CD的取值范围是 .
13.△ABC中,AC=8,BC=6,在△ABE中,DE为AB边上的高,DE=12,S△ABE=60,则AB= ,∠C= °.
14.如图,在Rt△ABC中,∠A=90°,AB=3,BC=5,BC的垂直平分线交AC于点D,垂足为点E,则AD= .
15.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,若AD=3,BC=5,则AB2+CD2= .
16.如图,“赵爽弦图”由4个完全一样的直角三角形所围成,在Rt△ABC中,AC=b,BC=a,∠ACB=90°,若图中大正方形的面积为34,小正方形的面积为4,则a+b的值为 .
三.解答题(共6小题,满分40分)
17.如图,A,B,H是直线上的三个点,AC⊥l于点A,BD⊥l于点B,HC=HD,AB=5,AC=2,BD=3,求AH的长.
18.如图,Rt△ABC中,∠B=90°,AB=12,BC=16,CD=21,AD=29,点E是AD的中点,求CE的长.
19.如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若动点P从点A出发,沿着三角形的三边,先运动到点C,再运动到点B,最后运动回到点A,Vp=2cm/s,设点P的运动时间为ts.
(1)当t为何值时,点P恰好在AB的垂直平分线上?
(2)当t为何值时,点P在BC上,且恰好在∠BAC的角平分线上?
20.如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
(1)求AB和DE的长;
(2)求△ADB的面积.
21.如图,在△ABC中,AB=AC,AD⊥BC于点D,∠CBE=45°,BE分别交AC,AD于点E、F,连接CF.
(1)判断△BCF的形状,并说明理由;
(2)若AF=BC,求证:BF2+EF2=AE2.
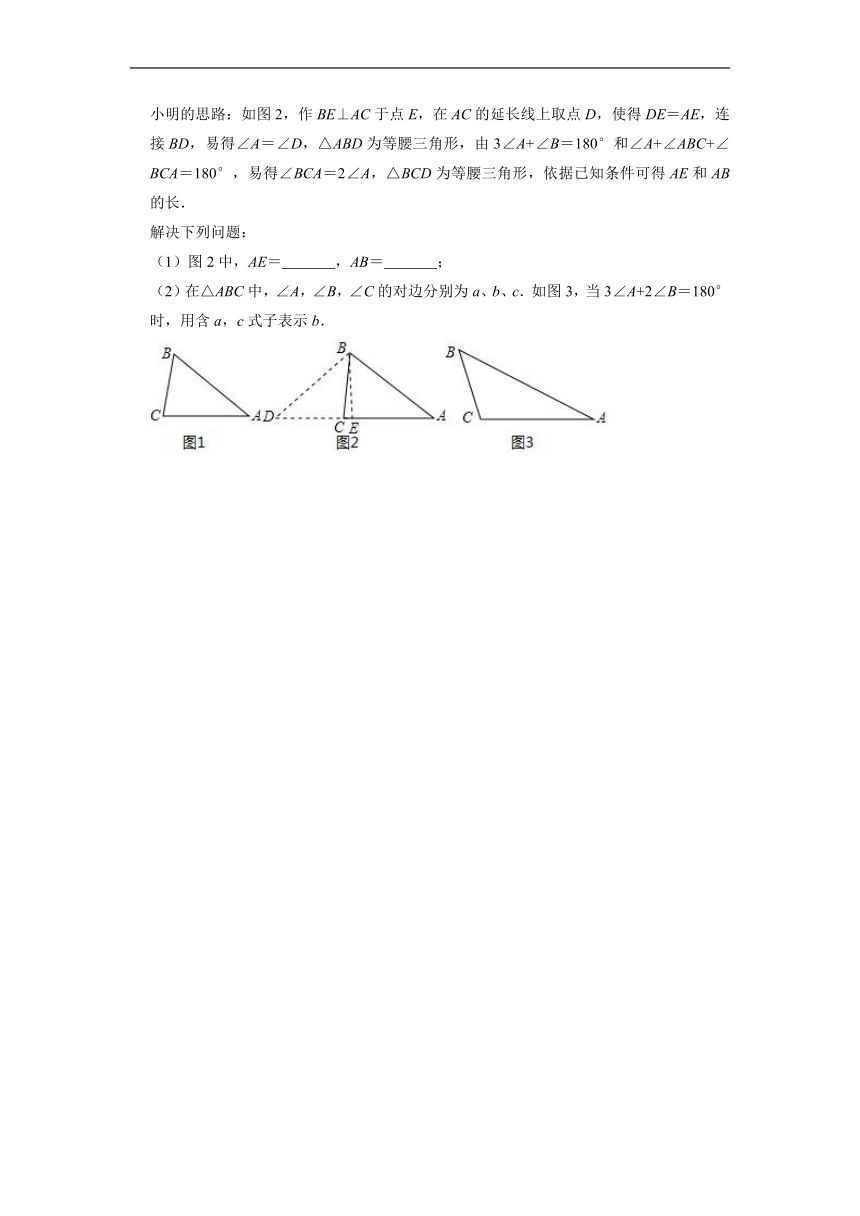
22.阅读:如图1,在△ABC中,3∠A+∠B=180°,BC=8,AC=10,求AB的长.
小明的思路:如图2,作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,易得∠A=∠D,△ABD为等腰三角形,由3∠A+∠B=180°和∠A+∠ABC+∠BCA=180°,易得∠BCA=2∠A,△BCD为等腰三角形,依据已知条件可得AE和AB的长.
解决下列问题:
(1)图2中,AE= ,AB= ;
(2)在△ABC中,∠A,∠B,∠C的对边分别为a、b、c.如图3,当3∠A+2∠B=180°时,用含a,c式子表示b.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵∠C=90°,a2=9,b2=16,
∴c2=a2+b2=9+16=25.
故选:C.
2.解:由勾股定理得:=5(cm),
∴阴影部分的面积=5×1=5(cm2);
故选:B.
3.解:由勾股定理得,
AC2=AB2+BC2=4+16=20,
∴正方形ADEC的面积为20,
故选:C.
4.解:∵∠ACB=90°,AC=5,
∴AB2﹣BC2=AC2=25,
∴正方形ABDE和正方形CBGF的面积差为AB2﹣BC2=25.
故选:D.
5.解:在Rt△ABC中,∠C=90°,a、b、c为三边,
∴a2+b2=c2,a+b>c,c﹣a<b,c﹣b<a,
∴选项A,B,D正确,
故选:C.
6.解:如图1,∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AB=20,AD=12,
∴BD=16,
又∵AC=13,
∴CD=5,
∴BC=BD+CD=21,
∴△ABC的面积=×21×12=126;
如图2,BC=BD﹣CD=11,
∴△ABC的面积=×11×12=66;
综上所述,△ABC的面积为126或66,
故选:D.
7.解:∵正方形ABCD的面积为15,
∴BC2=15,∠ABC=90°,
∴∠EBC=90°,
在Rt△BCE中,由勾股定理得:BE=7,
故选:D.
8.解:∵大正方形的面积为S1,小正方形的面积为S2,
∴a2+b2=S1,(b﹣a)2=S2,
∴4个直角三角形的面积=4×ab=2ab=S1﹣S2,
∴(a+b)2=a2+b2+2ab=S1+S1﹣S2=2S1﹣S2,
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵在Rt△ABC中,斜边BC=10,
∴AB2+AC2=BC2=100,
∴BC2+AB2+AC2=2BC2=200.
故答案是:200.
10.解:由图形可知,BC=5,BC边上的高为3,
∴△ABC的面积=×5×3=,
由勾股定理得,AC=5,
则×5×BD=,
解得,BD=3,
故答案为:3.
11.解:设AC=m,BC=n,
则S1=m2,S2=n2,S1+S2=m2+n2=60,
因为AB=10,即m+n=10,
所以(m+n)2=100,
m2+n2+2mn=100,
2mn=100﹣60=40,
mn=20,
所以S△BCD=mn==10.
故图中阴影部分的面积为10.
故答案为:10.
12.解:过点C作CD′⊥AB于D′,
由垂线段最短可知,当CD⊥AB时,CD最短,即点D在点D′的位置时,CD最短,
由勾股定理得:AC=8,
∵S△ABC=AB×CD′=AC,
∴CD′==4.8,
∴4.8≤CD≤8,
故答案为:4.8≤CD≤8.
13.解:∵S△ABE=60,
∴AB DE=60,即×AB×12=60,
解得:AB=10,
∵AC2+BC2=82+62=100,AB2=102=100,
∴AC2+BC2=AB2,
∴∠C=90°,
故答案为:10,90.
14.解:∵BC的垂直平分线交AC于点D,
∴BD=CD,
在Rt△ABC中,由勾股定理得,AC=4,
设AD=x,则CD=BD=4﹣x,
在Rt△ABD中,由勾股定理得,
x2+32=(4﹣x)2,
解得x=,
∴AD=,
故答案为:.
15.解:∵四边形ABCD为“垂美”四边形,
∴BD⊥AC,
∴∠AEB=∠AED=∠BEC=∠DEC=90°,
在Rt△AED中,AE2+DE2=AD2=9,
在Rt△BEC中,BE2+CE2=BC2=25,
∴AE2+DE2+BE2+CE2=9+25=34,
在Rt△AEB中,AE2+BE2=AB2,
在Rt△CED中,CE2+DE2=CD2,
∴AB2+CD2=AE2+DE2+BE2+CE2=9+25=34,
故答案为:34.
16.解:∵大正方形的面积为34,小正方形的面积为4,
∴a2+b2=34,(b﹣a)2=4,
∴4×ab=34﹣4=30,
∴2ab=30,
∴(a+b)2=(b﹣a)2+4ab=4+60=64,
∴a+b=8.
故答案为:8.
三.解答题(共6小题,满分40分)
17.解:∵AC⊥l于点A,BD⊥l于点B,
∴∠CAH=∠HBD=90°,
∵A,B,H是直线上的三个点,
∴AH+BH=AB=5,
∴BH=5﹣AH,
在Rt△ACH中,AC2+AH2=CH2,
即4+AH2=CH2,
在Rt△BHD中,BH2+BD2=DH2,
即(5﹣AH)2+9=DH2,
∵HC=HD,
∴4+AH2=(5﹣AH)2+9,
∴AH=3,
故AH的长为3.
18.解:在Rt△ABC中,∠B=90°,
∵AB=12,BC=16,
∴AC=20,
∵CD=21,AD=29,
∵AC2+CD2=202+212=841,
AD2=841,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴△ACD是直角三角形,
∵点E是AD的中点,
∴CE==×29=.
19.解:(1)当点P在AC上时,连接PB,
由勾股定理得AC=8,
∵点P恰好在AB的垂直平分线上,
∴PA=PB=2t,
∴(8﹣2t)2+62=(2t)2,
解得t=,
当P在AB上时,PA=PB=5,
∴点P运动的路程为8+6+5=19,
∴t=,
∴t=或时,点P恰好在AB的垂直平分线上;
(2)过点P作PF⊥AB于F,则PF=PC=2t﹣8,
在Rt△BPF中,由勾股定理得,
(2t﹣8)2+22=(14﹣2t)2,
解得t=,
∴t=时,点P在BC上,且恰好在∠BAC的角平分线上.
20.解:(1)∵∠C=90°,
∴AB=10;
∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE,
∵CD=3,
∴DE=3;
(2)由(1)知,AB=10,
∴△ADB的面积为S△ADB=AB DE=×10×3=15.
21.(1)解:△BCF为等腰直角三角形.
理由:∵AB=AC,AD⊥BC,
∴BD=CD,
∴AD垂直平分BC,
∴BF=CF,
∴∠BCF=∠CBF=45°,
∴∠CFB=180°﹣45°﹣45°=90°,
∴△BCF为等腰直角三角形;
(2)证明:在BF上取一点H,使BH=EF,连接CH,
在△CHB和△AEF中,
,
∴△CHB≌△AEF(SAS),
∴AE=CH,∠AEF=∠BHC,
∴∠CEF=∠CHE,
∴CE=CH,
∵BD=CD,FD⊥BC,
∴CF=BF,
∴∠CFD=∠BFD=45°,
∴∠CFB=90°,
∴EF=FH,
Rt△CFH中,由勾股定理得:CF2+FH2=CH2,
∴BF2+EF2=AE2.
22.解:(1)如图2,作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,
则BE是AD的垂直平分线,
∴AB=BD,∠A=∠D,
∵3∠A+∠ABC=180°,∠A+∠ABC+∠BCA=180°,
∴∠BCA=2∠A,
∵∠BCA=∠D+∠CBD,
∴∠BCA=∠A+∠CBD=2∠A,
∴∠CBD=∠A,
∴DC=BC=8,
∴AD=DC+AC=8+10=18,
∴AE=AD=9,
∴EC=AD﹣CD=9﹣8=1.
∴在直角△BCE和直角△AEB中,
由勾股定理得到:BC2﹣CE2=AB2﹣AE2,即82﹣12=AB2﹣92,
解得,AB=12,
故答案是:9;12;
(2)作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,
则BE是边AD的垂直平分线,
∴AB=BD,∠A=∠D.
∵3∠A+2∠B=180°,∠A+∠ABC+∠BCA=180°,
∴2∠A+∠ABC=∠ACB,
∵∠ACB=∠D+∠DBC,
∴2∠A+∠ABC=∠D+∠DBC,
∵∠A=∠D,
∴∠A+∠ABC=∠DBC,BD=AB=c,即∠DCB=∠DBC,
∴DB=DC=c,
由题意得,DE=AE=,
∴EC=AE﹣AC=﹣b=,
在Rt△BEC中,BE2=BC2﹣EC2,
在Rt△BEA中,BE2=BA2﹣EA2,
∴BC2﹣EC2=BA2﹣EA2,即a2﹣()2=c2﹣()2,
整理得,b=.
一.选择题(共8小题,满分40分)
1.直角三角形的边长分别为a,b,c,且∠C=90°,若a2=9,b2=16,那么c2的值是( )
A.5 B.7 C.25 D.49
2.如图,阴影部分是一个长方形,则长方形的面积是( )
A.4cm2 B.5cm2 C.6cm2 D.12cm2
3.如图,在△ABC中,∠B=90°,AB=2、BC=4,四边形ADEC是正方形,则正方形ADEC的面积是( )
A.8 B.16 C.20 D.25
4.如图,在Rt△ABC中,∠ACB=90°.若AC=5,则正方形ABDE和正方形CBGF的面积差为( )
A.10 B.15 C.20 D.25
5.在Rt△ABC中,∠C=90°,a、b、c为三边,则下列关系不正确的是( )
A.a2+b2=c2 B.a+b>c C.c﹣a>b D.c﹣b<a
6.△ABC中,AB=20,AC=13,高AD=12,则△ABC的面积为( )
A.66 B.126 C.54或44 D.126或66
7.如图,正方形ABCD的面积为15,Rt△BCE的斜边CE的长为8,则BE的长为( )
A.17 B.10 C.6 D.7
8.如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼接成的大正方形,若直角三角形的两条直角边长分别为a,b(a>b),大正方形的面积为S1,小正方形的面积为S2,则用含S1,S 的代数式表示(a+b)2正确的是( )
A.S1 B.S2 C.2S1﹣S2 D.2S2﹣S1
二.填空题(共8小题,满分40分)
9.在Rt△ABC中,斜边BC=10,则BC2+AB2+AC2= .
10.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为 .
11.如图,点C是线段AB上一点,以AC、BC为边向两边作正方形ACDE和BCFG,已知AB=10,两正方形的面积和S1+S2=60,则图中阴影部分的面积为 .
12.如图,已知△ABC中,∠C=90°,AB=10,BC=6,若点D为AB边上任意一点,则线段CD的取值范围是 .
13.△ABC中,AC=8,BC=6,在△ABE中,DE为AB边上的高,DE=12,S△ABE=60,则AB= ,∠C= °.
14.如图,在Rt△ABC中,∠A=90°,AB=3,BC=5,BC的垂直平分线交AC于点D,垂足为点E,则AD= .
15.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,若AD=3,BC=5,则AB2+CD2= .
16.如图,“赵爽弦图”由4个完全一样的直角三角形所围成,在Rt△ABC中,AC=b,BC=a,∠ACB=90°,若图中大正方形的面积为34,小正方形的面积为4,则a+b的值为 .
三.解答题(共6小题,满分40分)
17.如图,A,B,H是直线上的三个点,AC⊥l于点A,BD⊥l于点B,HC=HD,AB=5,AC=2,BD=3,求AH的长.
18.如图,Rt△ABC中,∠B=90°,AB=12,BC=16,CD=21,AD=29,点E是AD的中点,求CE的长.
19.如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若动点P从点A出发,沿着三角形的三边,先运动到点C,再运动到点B,最后运动回到点A,Vp=2cm/s,设点P的运动时间为ts.
(1)当t为何值时,点P恰好在AB的垂直平分线上?
(2)当t为何值时,点P在BC上,且恰好在∠BAC的角平分线上?
20.如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
(1)求AB和DE的长;
(2)求△ADB的面积.
21.如图,在△ABC中,AB=AC,AD⊥BC于点D,∠CBE=45°,BE分别交AC,AD于点E、F,连接CF.
(1)判断△BCF的形状,并说明理由;
(2)若AF=BC,求证:BF2+EF2=AE2.
22.阅读:如图1,在△ABC中,3∠A+∠B=180°,BC=8,AC=10,求AB的长.
小明的思路:如图2,作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,易得∠A=∠D,△ABD为等腰三角形,由3∠A+∠B=180°和∠A+∠ABC+∠BCA=180°,易得∠BCA=2∠A,△BCD为等腰三角形,依据已知条件可得AE和AB的长.
解决下列问题:
(1)图2中,AE= ,AB= ;
(2)在△ABC中,∠A,∠B,∠C的对边分别为a、b、c.如图3,当3∠A+2∠B=180°时,用含a,c式子表示b.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵∠C=90°,a2=9,b2=16,
∴c2=a2+b2=9+16=25.
故选:C.
2.解:由勾股定理得:=5(cm),
∴阴影部分的面积=5×1=5(cm2);
故选:B.
3.解:由勾股定理得,
AC2=AB2+BC2=4+16=20,
∴正方形ADEC的面积为20,
故选:C.
4.解:∵∠ACB=90°,AC=5,
∴AB2﹣BC2=AC2=25,
∴正方形ABDE和正方形CBGF的面积差为AB2﹣BC2=25.
故选:D.
5.解:在Rt△ABC中,∠C=90°,a、b、c为三边,
∴a2+b2=c2,a+b>c,c﹣a<b,c﹣b<a,
∴选项A,B,D正确,
故选:C.
6.解:如图1,∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AB=20,AD=12,
∴BD=16,
又∵AC=13,
∴CD=5,
∴BC=BD+CD=21,
∴△ABC的面积=×21×12=126;
如图2,BC=BD﹣CD=11,
∴△ABC的面积=×11×12=66;
综上所述,△ABC的面积为126或66,
故选:D.
7.解:∵正方形ABCD的面积为15,
∴BC2=15,∠ABC=90°,
∴∠EBC=90°,
在Rt△BCE中,由勾股定理得:BE=7,
故选:D.
8.解:∵大正方形的面积为S1,小正方形的面积为S2,
∴a2+b2=S1,(b﹣a)2=S2,
∴4个直角三角形的面积=4×ab=2ab=S1﹣S2,
∴(a+b)2=a2+b2+2ab=S1+S1﹣S2=2S1﹣S2,
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵在Rt△ABC中,斜边BC=10,
∴AB2+AC2=BC2=100,
∴BC2+AB2+AC2=2BC2=200.
故答案是:200.
10.解:由图形可知,BC=5,BC边上的高为3,
∴△ABC的面积=×5×3=,
由勾股定理得,AC=5,
则×5×BD=,
解得,BD=3,
故答案为:3.
11.解:设AC=m,BC=n,
则S1=m2,S2=n2,S1+S2=m2+n2=60,
因为AB=10,即m+n=10,
所以(m+n)2=100,
m2+n2+2mn=100,
2mn=100﹣60=40,
mn=20,
所以S△BCD=mn==10.
故图中阴影部分的面积为10.
故答案为:10.
12.解:过点C作CD′⊥AB于D′,
由垂线段最短可知,当CD⊥AB时,CD最短,即点D在点D′的位置时,CD最短,
由勾股定理得:AC=8,
∵S△ABC=AB×CD′=AC,
∴CD′==4.8,
∴4.8≤CD≤8,
故答案为:4.8≤CD≤8.
13.解:∵S△ABE=60,
∴AB DE=60,即×AB×12=60,
解得:AB=10,
∵AC2+BC2=82+62=100,AB2=102=100,
∴AC2+BC2=AB2,
∴∠C=90°,
故答案为:10,90.
14.解:∵BC的垂直平分线交AC于点D,
∴BD=CD,
在Rt△ABC中,由勾股定理得,AC=4,
设AD=x,则CD=BD=4﹣x,
在Rt△ABD中,由勾股定理得,
x2+32=(4﹣x)2,
解得x=,
∴AD=,
故答案为:.
15.解:∵四边形ABCD为“垂美”四边形,
∴BD⊥AC,
∴∠AEB=∠AED=∠BEC=∠DEC=90°,
在Rt△AED中,AE2+DE2=AD2=9,
在Rt△BEC中,BE2+CE2=BC2=25,
∴AE2+DE2+BE2+CE2=9+25=34,
在Rt△AEB中,AE2+BE2=AB2,
在Rt△CED中,CE2+DE2=CD2,
∴AB2+CD2=AE2+DE2+BE2+CE2=9+25=34,
故答案为:34.
16.解:∵大正方形的面积为34,小正方形的面积为4,
∴a2+b2=34,(b﹣a)2=4,
∴4×ab=34﹣4=30,
∴2ab=30,
∴(a+b)2=(b﹣a)2+4ab=4+60=64,
∴a+b=8.
故答案为:8.
三.解答题(共6小题,满分40分)
17.解:∵AC⊥l于点A,BD⊥l于点B,
∴∠CAH=∠HBD=90°,
∵A,B,H是直线上的三个点,
∴AH+BH=AB=5,
∴BH=5﹣AH,
在Rt△ACH中,AC2+AH2=CH2,
即4+AH2=CH2,
在Rt△BHD中,BH2+BD2=DH2,
即(5﹣AH)2+9=DH2,
∵HC=HD,
∴4+AH2=(5﹣AH)2+9,
∴AH=3,
故AH的长为3.
18.解:在Rt△ABC中,∠B=90°,
∵AB=12,BC=16,
∴AC=20,
∵CD=21,AD=29,
∵AC2+CD2=202+212=841,
AD2=841,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴△ACD是直角三角形,
∵点E是AD的中点,
∴CE==×29=.
19.解:(1)当点P在AC上时,连接PB,
由勾股定理得AC=8,
∵点P恰好在AB的垂直平分线上,
∴PA=PB=2t,
∴(8﹣2t)2+62=(2t)2,
解得t=,
当P在AB上时,PA=PB=5,
∴点P运动的路程为8+6+5=19,
∴t=,
∴t=或时,点P恰好在AB的垂直平分线上;
(2)过点P作PF⊥AB于F,则PF=PC=2t﹣8,
在Rt△BPF中,由勾股定理得,
(2t﹣8)2+22=(14﹣2t)2,
解得t=,
∴t=时,点P在BC上,且恰好在∠BAC的角平分线上.
20.解:(1)∵∠C=90°,
∴AB=10;
∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE,
∵CD=3,
∴DE=3;
(2)由(1)知,AB=10,
∴△ADB的面积为S△ADB=AB DE=×10×3=15.
21.(1)解:△BCF为等腰直角三角形.
理由:∵AB=AC,AD⊥BC,
∴BD=CD,
∴AD垂直平分BC,
∴BF=CF,
∴∠BCF=∠CBF=45°,
∴∠CFB=180°﹣45°﹣45°=90°,
∴△BCF为等腰直角三角形;
(2)证明:在BF上取一点H,使BH=EF,连接CH,
在△CHB和△AEF中,
,
∴△CHB≌△AEF(SAS),
∴AE=CH,∠AEF=∠BHC,
∴∠CEF=∠CHE,
∴CE=CH,
∵BD=CD,FD⊥BC,
∴CF=BF,
∴∠CFD=∠BFD=45°,
∴∠CFB=90°,
∴EF=FH,
Rt△CFH中,由勾股定理得:CF2+FH2=CH2,
∴BF2+EF2=AE2.
22.解:(1)如图2,作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,
则BE是AD的垂直平分线,
∴AB=BD,∠A=∠D,
∵3∠A+∠ABC=180°,∠A+∠ABC+∠BCA=180°,
∴∠BCA=2∠A,
∵∠BCA=∠D+∠CBD,
∴∠BCA=∠A+∠CBD=2∠A,
∴∠CBD=∠A,
∴DC=BC=8,
∴AD=DC+AC=8+10=18,
∴AE=AD=9,
∴EC=AD﹣CD=9﹣8=1.
∴在直角△BCE和直角△AEB中,
由勾股定理得到:BC2﹣CE2=AB2﹣AE2,即82﹣12=AB2﹣92,
解得,AB=12,
故答案是:9;12;
(2)作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,
则BE是边AD的垂直平分线,
∴AB=BD,∠A=∠D.
∵3∠A+2∠B=180°,∠A+∠ABC+∠BCA=180°,
∴2∠A+∠ABC=∠ACB,
∵∠ACB=∠D+∠DBC,
∴2∠A+∠ABC=∠D+∠DBC,
∵∠A=∠D,
∴∠A+∠ABC=∠DBC,BD=AB=c,即∠DCB=∠DBC,
∴DB=DC=c,
由题意得,DE=AE=,
∴EC=AE﹣AC=﹣b=,
在Rt△BEC中,BE2=BC2﹣EC2,
在Rt△BEA中,BE2=BA2﹣EA2,
∴BC2﹣EC2=BA2﹣EA2,即a2﹣()2=c2﹣()2,
整理得,b=.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
