2022—2023学年人教版数学八年级上册11.2.2 三角形的外角 同步精练(word、含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.2.2 三角形的外角 同步精练(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 599.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-03 18:17:29 | ||
图片预览



文档简介
11.2.2 三角形的外角 同步精练
一、单选题
1.如图,∠1、∠2、∠3中是△ABC外角的是( )
A.∠1、∠2 B.∠2、∠3 C.∠1、∠3 D.∠1、∠2、∠3
2.如图,已知AB∥FE,,,则的值为( )
A. B. C. D.
3.如图,AB∥CD,∠A=38°,∠C=80°,则∠M为( )
A.52° B.42° C.10° D.40°
4.如图是一款手推车的平面示意图,其中AB∥CD,,,则的大小是( )
A. B. C. D.
5.如图,∠B=40°,∠ACD=108°,若B、C、D三点在一条直线上,则∠A的大小是( )
A.148° B.78° C.68° D.50°
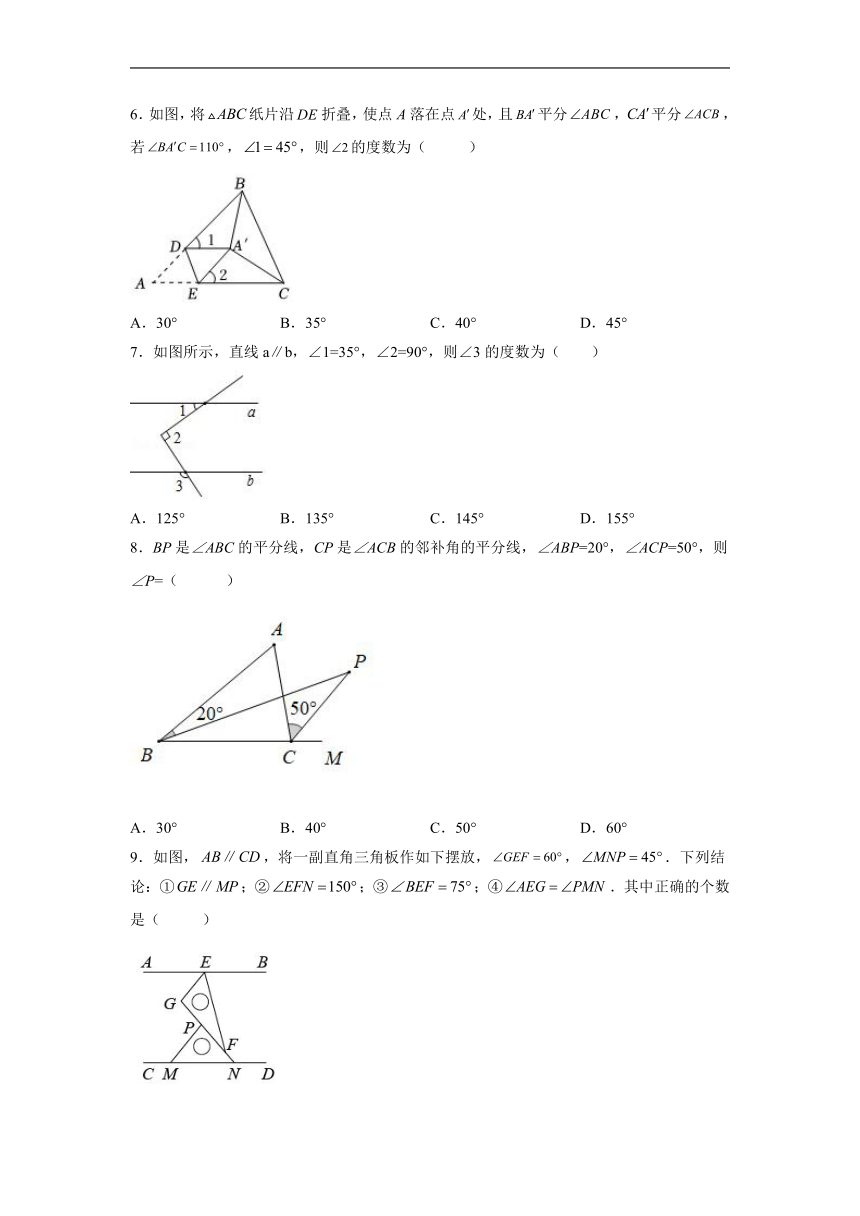
6.如图,将纸片沿折叠,使点A落在点处,且平分,平分,若,,则的度数为( )
A.30° B.35° C.40° D.45°
7.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
8.BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
9.如图,,将一副直角三角板作如下摆放,,.下列结论:①;②;③;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
10.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,是的外角.
求证:.
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
11.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A.①②③ B.①③④ C.①④ D.①②④
12.四边形ABCD两组对边AD,BC与AB,DC延长线分别交于点E,F,∠AEB,∠AFD的平分线交于点P,∠A=64°,∠BCD=136°,则下列结论中正确的是( )
①∠EPF=100°;②∠ADC+∠ABC=160°;③∠PEB+∠PFC+∠EPF=136°;④∠PEA+∠PFA=36°
A.①②③ B.②③④ C.①③④ D.①②③④
二、填空题
13.一副三角板如图所示摆放,且,则的度数为__________.
14.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D=______.
15.如图,在中,已知,,是上的高,是上的高,是和的交点,的度数是________.
16.如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_____.
17.①如图1,若,则;②如图2,若,则∠C;③如图3,若,则;④如图4,若,点O在直线EF上,则.以上结论正确的序号是_____.
三、解答题
18.如图,在中,,外角.求和的度数.
19.如图,在中,,,于D,点E为BC边上一点,连接AE.把沿着AE对折后,点B的对应点刚好落在AC边上的点F处.
(1)求∠FEC的度数;
(2)求∠DAE的度数.
20.平面内的两条直线有相交和平行两种位置关系
(1)AB//CD.如图a,点P在AB、CD外部时,∠B,∠BPD,∠D之间有何数量关系?请说明理由
(2)如图b,将点P移到AB、CD内部,∠BPD、∠B、∠D之间又有何数量关系?请说明理由
21.模型规律:如图1,延长交于点D,则.因为凹四边形形似箭头,其四角具有“”这个规律,所以我们把这个模型叫做“箭头四角形”.
模型应用
(1)直接应用:
①如图2,,则__________;
②如图3,__________;
(2)拓展应用:
①如图4,、的2等分线(即角平分线)、交于点,已知,,则__________;
②如图5,、分别为、的10等分线.它们的交点从上到下依次为、、、…、.已知,,则__________;
③如图6,、的角平分线、交于点D,已知,则__________;
④如图7,、的角平分线、交于点D,则、、之同的数量关系为__________。
参考答案
1--10CDBAC BAADB 11--12CD
13.
14.34°
15.120°
16.70°
17.①②④
18.解:由三角形外角的性质可得:
又∵,
∴
∵
∴
故答案为:,
19.(1)由折叠知∵, ∴;
(2)由(1)知,∴由对折知,∴∵,∴
20.(1)解:∠B=∠BPD+∠D,理由如下:
∵AB∥CD,
∴∠B=∠BOD,
又∵∠BOD=∠BPD+∠D,
∴∠B=∠BPD+∠D;
(2)∠BPD=∠B+∠D,理由如下:
延长BP交CD于点E,如图所示:
∵AB∥CD,
∴∠B=∠BED,
又∵∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D.
21.解:(1)①∠BOC=∠A+∠B+∠C=60°+20°+30°=110°;
②∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE=2×130°=260°;
(2)①∠BO1C=∠BOC-∠OBO1-∠OCO1
=∠BOC-(∠ABO+∠ACO)
=∠BOC-(∠BOC-∠A)
=∠BOC-(120°-50°)
=120°-35°
=85°;
②∠BO7C=∠BOC-(∠BOC-∠A)
=120°-(120°-50°)
=120°-21°
=99°;
③∠ADB=180°-(∠ABD+∠BAD)
=180°-(∠BOC-∠C)
=180°-(120°-44°)
=142°;
④∠BOD=∠BOC=∠B+∠D+∠BAC,
∠BOC=∠B+∠C+∠BAC,
联立得:∠B-∠C+2∠D=0.
一、单选题
1.如图,∠1、∠2、∠3中是△ABC外角的是( )
A.∠1、∠2 B.∠2、∠3 C.∠1、∠3 D.∠1、∠2、∠3
2.如图,已知AB∥FE,,,则的值为( )
A. B. C. D.
3.如图,AB∥CD,∠A=38°,∠C=80°,则∠M为( )
A.52° B.42° C.10° D.40°
4.如图是一款手推车的平面示意图,其中AB∥CD,,,则的大小是( )
A. B. C. D.
5.如图,∠B=40°,∠ACD=108°,若B、C、D三点在一条直线上,则∠A的大小是( )
A.148° B.78° C.68° D.50°
6.如图,将纸片沿折叠,使点A落在点处,且平分,平分,若,,则的度数为( )
A.30° B.35° C.40° D.45°
7.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
8.BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
9.如图,,将一副直角三角板作如下摆放,,.下列结论:①;②;③;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
10.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,是的外角.
求证:.
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
11.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A.①②③ B.①③④ C.①④ D.①②④
12.四边形ABCD两组对边AD,BC与AB,DC延长线分别交于点E,F,∠AEB,∠AFD的平分线交于点P,∠A=64°,∠BCD=136°,则下列结论中正确的是( )
①∠EPF=100°;②∠ADC+∠ABC=160°;③∠PEB+∠PFC+∠EPF=136°;④∠PEA+∠PFA=36°
A.①②③ B.②③④ C.①③④ D.①②③④
二、填空题
13.一副三角板如图所示摆放,且,则的度数为__________.
14.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D=______.
15.如图,在中,已知,,是上的高,是上的高,是和的交点,的度数是________.
16.如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_____.
17.①如图1,若,则;②如图2,若,则∠C;③如图3,若,则;④如图4,若,点O在直线EF上,则.以上结论正确的序号是_____.
三、解答题
18.如图,在中,,外角.求和的度数.
19.如图,在中,,,于D,点E为BC边上一点,连接AE.把沿着AE对折后,点B的对应点刚好落在AC边上的点F处.
(1)求∠FEC的度数;
(2)求∠DAE的度数.
20.平面内的两条直线有相交和平行两种位置关系
(1)AB//CD.如图a,点P在AB、CD外部时,∠B,∠BPD,∠D之间有何数量关系?请说明理由
(2)如图b,将点P移到AB、CD内部,∠BPD、∠B、∠D之间又有何数量关系?请说明理由
21.模型规律:如图1,延长交于点D,则.因为凹四边形形似箭头,其四角具有“”这个规律,所以我们把这个模型叫做“箭头四角形”.
模型应用
(1)直接应用:
①如图2,,则__________;
②如图3,__________;
(2)拓展应用:
①如图4,、的2等分线(即角平分线)、交于点,已知,,则__________;
②如图5,、分别为、的10等分线.它们的交点从上到下依次为、、、…、.已知,,则__________;
③如图6,、的角平分线、交于点D,已知,则__________;
④如图7,、的角平分线、交于点D,则、、之同的数量关系为__________。
参考答案
1--10CDBAC BAADB 11--12CD
13.
14.34°
15.120°
16.70°
17.①②④
18.解:由三角形外角的性质可得:
又∵,
∴
∵
∴
故答案为:,
19.(1)由折叠知∵, ∴;
(2)由(1)知,∴由对折知,∴∵,∴
20.(1)解:∠B=∠BPD+∠D,理由如下:
∵AB∥CD,
∴∠B=∠BOD,
又∵∠BOD=∠BPD+∠D,
∴∠B=∠BPD+∠D;
(2)∠BPD=∠B+∠D,理由如下:
延长BP交CD于点E,如图所示:
∵AB∥CD,
∴∠B=∠BED,
又∵∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D.
21.解:(1)①∠BOC=∠A+∠B+∠C=60°+20°+30°=110°;
②∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE=2×130°=260°;
(2)①∠BO1C=∠BOC-∠OBO1-∠OCO1
=∠BOC-(∠ABO+∠ACO)
=∠BOC-(∠BOC-∠A)
=∠BOC-(120°-50°)
=120°-35°
=85°;
②∠BO7C=∠BOC-(∠BOC-∠A)
=120°-(120°-50°)
=120°-21°
=99°;
③∠ADB=180°-(∠ABD+∠BAD)
=180°-(∠BOC-∠C)
=180°-(120°-44°)
=142°;
④∠BOD=∠BOC=∠B+∠D+∠BAC,
∠BOC=∠B+∠C+∠BAC,
联立得:∠B-∠C+2∠D=0.
