第二十三章 旋转单元测试卷(含答案)

第二十三章 旋转 单元测试卷
学校:___________姓名：___________班级：___________考号：___________
一、单选题(每小题4分，共10各小题，共计40分)
1．已知点经变换后到点B，下面的说法正确的是（ ）
A．点A与点B关于x轴对称，则点B的坐标为
B．点A绕原点按顺时针方向旋转90°后到点B，则点B的坐标为
C．点A与点B关于原点中心对称，则点B的坐标为
D．点A先向上平移3个单位，再向右平移4个单位到点B，则点B的坐标为
2．如图，正方形的边长为，将正方形绕原点O顺时针旋转45°，则点B的对应点的坐标为（ ）
A． B． C． D．
3．点M位于平面直角坐标系第四象限，且到x轴的距离是5，到y轴的距离是2，则点M关于原点对称的的坐标是（　　　）
A．（2，－5） B．（－2，5） C．（5，－2） D．（－5，2）
4．如图，将△ABC绕点B顺时针旋转一定的角度得到，此时点C在边上，若AB＝5，＝2，则的长是（ ）
A．2 B．3 C．4 D．5
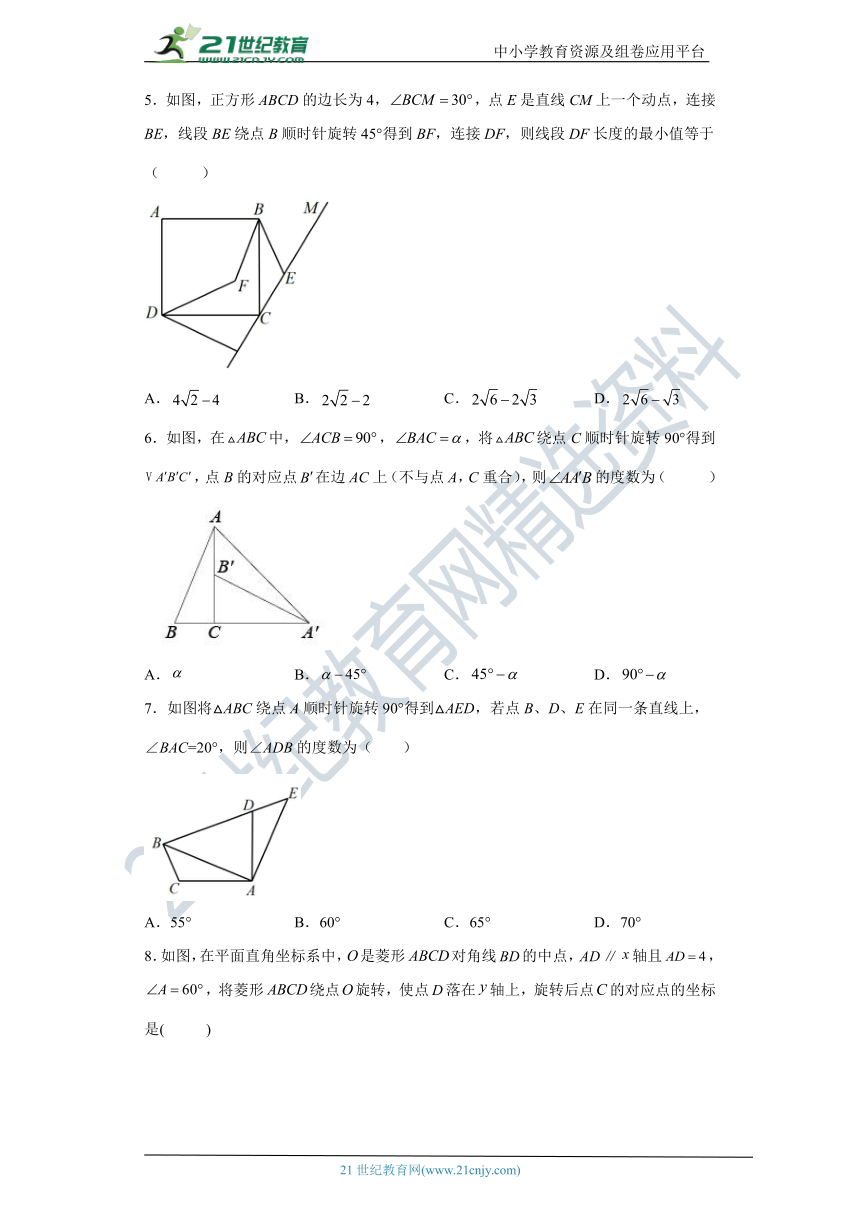
5．如图，正方形ABCD的边长为4，，点E是直线CM上一个动点，连接BE，线段BE绕点B顺时针旋转45°得到BF，连接DF，则线段DF长度的最小值等于（ ）
A． B． C． D．
6．如图，在中，，，将绕点C顺时针旋转90°得到，点B的对应点在边AC上（不与点A，C重合），则的度数为（ ）
A． B． C． D．
7．如图将△ABC绕点A顺时针旋转90°得到△AED，若点B、D、E在同一条直线上，∠BAC=20°，则∠ADB的度数为（ ）
A．55° B．60° C．65° D．70°
8．如图，在平面直角坐标系中，是菱形对角线的中点，轴且，，将菱形绕点旋转，使点落在轴上，旋转后点的对应点的坐标是( )
B．或
C． D．或
9．如图，在平面直角坐标系中，有一只蜗牛从点的位置沿着射线的方向爬行到另一象限的点，恰好，则点的坐标为（ ）
A． B． C． D．
10．如图，与关于点成中心对称，则下列结论不成立的是（ ）
A．点与点是对称点 B．
C． D．
二、填空题(每小题5分，共5各小题，共计25分)
11．如图，已知四边形是平行四边形，将边绕点D逆时针旋转60°得到，线段交边于点F，连接．若，，，则线段的长为_______．
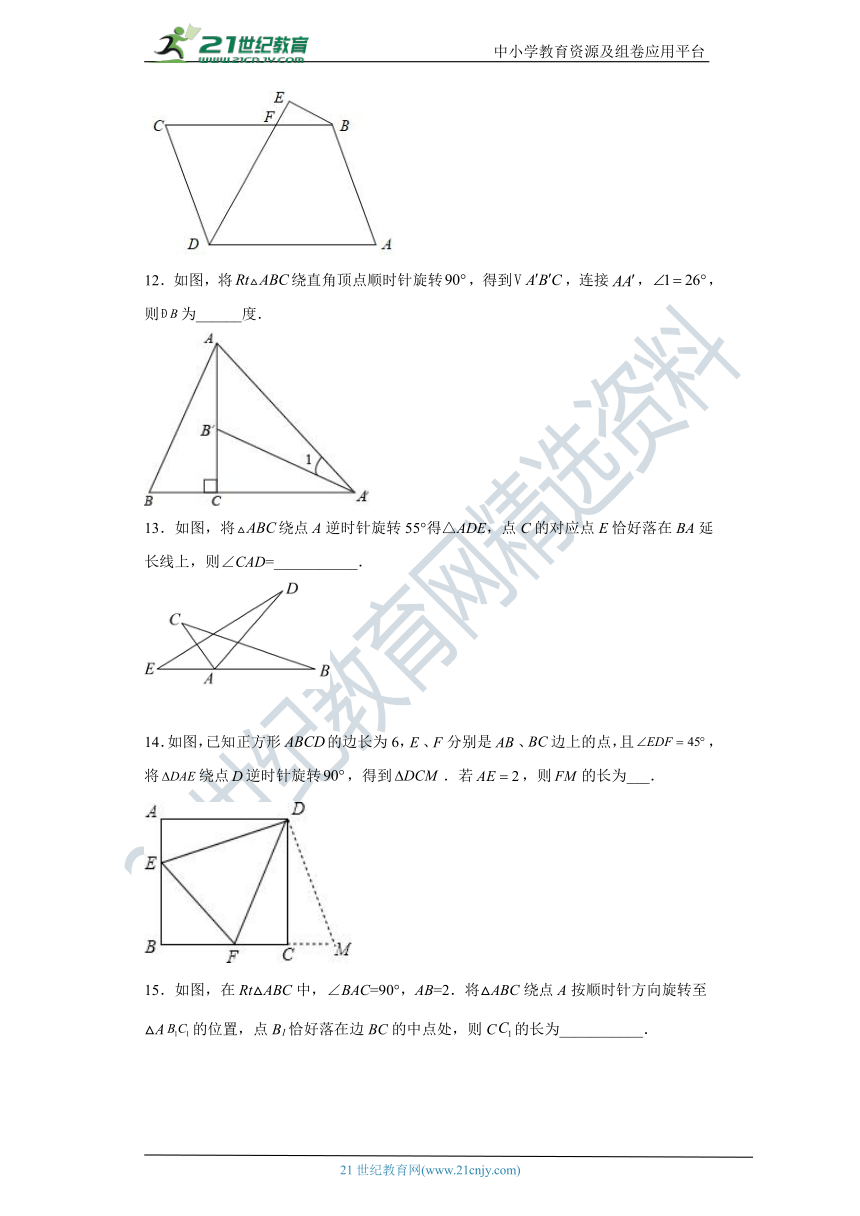
12．如图，将绕直角顶点顺时针旋转，得到，连接，，则为______度．
13．如图，将绕点A逆时针旋转55°得△ADE，点C的对应点E恰好落在BA延长线上，则∠CAD=___________．
14．如图，已知正方形的边长为6，、分别是、边上的点，且，将绕点逆时针旋转，得到．若，则的长为___．
15．如图，在Rt△ABC中，∠BAC=90°，AB=2．将△ABC绕点A按顺时针方向旋转至△A的位置，点B1恰好落在边BC的中点处，则C的长为___________．
三、解答题(16、17、18题9分，19题8分，共计35分)
16．如图，点A、B、C都在网格格点上，三个顶点的坐标分别为．
(1)经过平移得到，点A、B、C的对应点分别为、、，中任意一点平移后的对应点为．请在图中作出；
(2)请在图中作出关于原点O对称的，点A、B、C的对应点分别为、、．
17．如图，在中，，点为边的中点，连接，将绕点顺时针方向旋转，得到，点，的对应点分别为点，，连接，．求证：．
18．如图，在中，，点D是边上一点，连接，将线段绕点C逆时针旋转至，连接，取的中点M，连接．
(1)求证：；
(2)问与有何数量关系？写出你的结论并证明；
(3)若点D在上运动，则四边形能否形成平行四边形？若能，请直接写出此时的长；若不能，说明理由．
19．如图，将矩形ABCD绕点C顺时针旋转，得到矩形FGCE，使得点E落在边AB上，AB的延长线交EG于H，连接DE，DH．
(1)求证：ED平分；
(2)求证：EC与DH互相平分；
(3)设EC与DH相交于点O，，求点O到DC的距离．
中小学教育资源及组卷应用平台
试卷第1页，共3页
21世纪教育网(www.21cnjy.com)
参考答案：
1．D【分析】根据点坐标的轴对称与平移变换、点坐标的旋转变换与中心对称变换逐项判断即可得．
【详解】解：A、点与点关于轴对称，则点的坐标为，则此项错误，不符合题意；
B、点绕原点按顺时针方向旋转后到点，则横、纵坐标互换位置，且纵坐标变为相反数，所以点的坐标为，则此项错误，不符合题意；
C、点与点关于原点中心对称，则点的坐标为，则此项错误，不符合题意；
D、点先向上平移3个单位，再向右平移4个单位到点，则点的坐标为，即为，则此项正确，符合题意；
故选：D．
【点睛】本题考查了点坐标的轴对称与平移变换、点坐标的旋转变换与中心对称变换，熟练掌握点坐标的变换规律是解题关键．
2．D【分析】连接OB，由正方形ABCD绕原点O顺时针旋转45°，推出，得到△为等腰直角三角形，点在y轴上，利用勾股定理求出O即可．
【详解】解：连接OB，
∵正方形ABCD绕原点O顺时针旋转45°，
∴，，
∴，
∴△为等腰直角三角形，点在y轴上，
∵，
∴=2，
∴（0，2），
故选：D．
【点睛】本题考查了正方形的性质，旋转的性质，特殊三角形的性质．关键是根据旋转角证明点B1在y轴上．
3．B【分析】可先根据题意得到点M的坐标；然后由“两个点关于原点对称时，它们的坐标符号相反”得到的坐标．
【详解】解：∵M到x轴的距离为5，到y轴的距离为2，
∴M纵坐标可能为±5，横坐标可能为±2，
∵点M在第四象限，
∴M坐标为（2， 5）．
∴点M关于原点对称的的坐标是（ 2，5）．
故选：B．
【点睛】本题考查点的坐标的确定；用到的知识点为：点到x轴的距离为点的纵坐标的绝对值，到y轴的距离为点的横坐标的绝对值；两个点关于原点对称时，它们的坐标符号相反．
4．B【分析】由旋转的性质可得AB＝＝5，BC＝＝2，即可求解．
【详解】解：∵将△ABC绕点B顺时针旋转一定的角度得到，
∴AB＝＝5，BC＝＝2，
∴＝－BC＝3，
故选：B．
【点睛】本题考查了旋转的性质，掌握旋转的性质是解题的关键．
5．B【分析】连接BD，在BD上截取BG＝BC，连接FG，过点D作于点H．利用正方形的性质、勾股定理得出，利用旋转的性质得出，，再证明，得出，可知点F在直线GF上运动，点F与点H重合时，DF的值最小，进而求出DH的值即可．
【详解】解：如图，连接BD，在BD上截取BG＝BC，连接FG，过点D作于点H．
∵四边形ABCD是正方形，边长为4，
∴，，，
∴，，
∴，
∵线段BE绕点B顺时针旋转45°得到BF，
∴，，
∴，
∴，
在和中，
，
∴，
∴，
∴点F在直线GF上运动，点F与点H重合时，DF的值最小，
∵，，
∴，
∴DF的最小值为．
故选B．
【点睛】本题考查正方形的性质，勾股定理，旋转的性质，全等三角形的判定与性质，以及垂线段最短等知识点，通过得出点F的运动轨迹是解题的关键．
6．C【分析】由旋转的性质可得，，进而可得，然后问题可求解．
【详解】解：由旋转的性质可得：，，
∴等腰直角三角形，
∴，
∴；
故选C．
【点睛】本题主要考查旋转的性质，熟练掌握旋转的性质是解题的关键．
7．C【分析】由旋转的性质可得∠BAC＝∠DAE＝20°，AB＝AE，∠BAE＝90°，根据三角形的外角的性质可求∠ADB的度数．
【详解】解：∵将△ABC绕点A顺时针旋转90°得到△AED，
∴∠BAC＝∠DAE＝20°，AB＝AE，∠BAE＝90°
∴∠BEA＝45°
∵∠BDA＝∠BEA＋∠DAE
∴∠BDA＝45°+20°＝65°
故选：C．
【点睛】本题考查了旋转的性质和三角形外角的性质，熟练运用旋转的性质解决问题是本题的关键．
8．D【分析】分点旋转到轴正半轴和轴负半轴两种情况分别讨论，结合菱形的性质求解．
【详解】解：根据菱形的对称性可得：当点旋转到轴正半轴时，
A、、均在坐标轴上，如下图，
，，
，
，
，
点的坐标为，
同理：当点旋转到轴负半轴时，
点的坐标为，
点的坐标为或，
故选：D．
【点睛】本题考查了菱形的对称性，坐标与图形变化，旋转的性质，直角三角形的性质和勾股定理等知识，解题的关键是要分情况讨论．
9．B【分析】根据题意可得，点与点A关于原点对称，根据关于原点对称的点的横坐标、纵坐标均为相反数作答即可．
【详解】，且点在射线上，
点与点A关于原点对称，
点的坐标为．
故选：B．
【点睛】本题考查了坐标确定位置，关于原点对称的点的坐标特点，熟练掌握知识点并能够运用数形结合的思想是解题的关键．
10．D【分析】根据中心对称的性质判断即可．
【详解】解：与△关于点成中心对称，
点与是一组对称点，，，
A，B，C都不合题意．
与不是对应角，
不成立．
故选：D．
【点睛】本题考查中心对称的性质，解题的关键是掌握中心对称的性质．
11．【分析】连接AE，过E作EG⊥AB于G，由旋转的性质得出DE=DA，∠ADE=60°，证出△ADE是等边三角形，由等边三角形的性质得出AE=AD，证出∠GBE=45°，由等腰直角三角形的性质及勾股定理可得出答案．
【详解】解：连接AE，过E作EG⊥AB于G，
∵四边形ABCD是平行四边形，
∴AB=CD=4，∠BAD=∠C，
∵将边AD绕点D逆时针旋转60°得到DE，
∴DE=DA，∠ADE=60°，
∴△ADE是等边三角形，
∴AE=AD，
∴AE=BC，
∵∠C+∠BEF=165°，
∴∠DAB+∠BEF=165°，
∴∠ABE=360°-（∠ADE+∠BEF+∠DAB）=135°，
∴∠GBE=45°，
∴BG=GE=BE=，
∴AG=AB+BG=4+=5，
∴BC=AE=．
故答案为：2．
【点睛】本题考查了平行四边形的性质，等边三角形的判定和性质，勾股定理，旋转的性质，熟练掌握旋转的性质是解题的关键．
12．71【分析】根据旋转的性质可得，然后判断出△是等腰直角三角形，根据等腰直角三角形的性质可得= 45°，再根据三角形的一个外角等于与它不相邻的两个内角的和求出，然后根据旋转的性质可得．
【详解】解：Rt△ABC绕直角顶点C顺时针旋转90°得到△A'B'C，
AC = A'C，
△是等腰直角三角形，
= 45°，
，
由旋转的性质得．
故答案为：．
【点睛】本题考查了旋转的性质，等腰直角三角形的判定与性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质并准确识图是解题的关键．
13．70°##70度【分析】利用旋转的性质得∠EAC=∠DAB=55°，然后利用平角的性质得到∠CAD=180°-∠EAC-∠DAB=180°-55°-55°=70°，
【详解】解：∵将△ABC绕点A逆时针旋转55°得△ADE，
∴∠EAC=∠DAB=55°，
∴∠CAD=180°-∠EAC-∠DAB=180°-55°-55°=70°，
故答案为：70°．
【点睛】考查了旋转的性质，解题的关键是了解∠EAC=∠DAB=55°，难度不大．
14．5【分析】根据旋转的性质可得，，AE=CM=2，、、三点共线，可证得，设，在中，由勾股定理，即可求解．
【详解】解：根据题意得：∠DAE=∠DCF=∠DCM=90°，
逆时针旋转得到，
，，，AE=CM=2，
、、三点共线，
，
，
，
在和中，
，
，
，
设，
，且，
，，
，
，
在中，由勾股定理得，
即，
解得：，
．
故答案为：5．
【点睛】本题主要考查了图形的旋转，正方形的性质，勾股定理，全等三角形的判定和性质，熟练掌握图形的旋转的性质，正方形的性质，勾股定理，全等三角形的判定和性质是解题的关键．
15．【分析】由旋转的性质及直角三角形的性质得出△是等边三角形，求出CA的长，则可得出答案．
【详解】解：∵在Rt△ABC中，∠BAC=90°，将该三角形绕点A按顺时针方向旋转到△的位置，点恰好落在边BC的中点处，
∴，=，AB=，，
∴=AB=＝，
∴△是等边三角形，
∴∠=∠B=60°，
∴，
∴∠=90°－＝60°，∠＝，
∵将△ABC绕点A按顺时针方向旋转至△的位置，
∴CA=，
∴△是等边三角形，
∴，
∵AB=2，
∴BC＝2AB＝4，
∴，
∴．
故答案为：．
【点睛】此题主要考查了旋转的性质，直角三角形的性质，等边三角形的判定与性质、勾股定理等知识，得出△AB是等边三角形是解题关键．
16．(1)见解析
(2)见解析
【分析】（1）由点P（x1，y1）平移后的对应点为P1（x1+4，y1+3）得出平移的方式为向右平移4个单位、向上平移3个单位，据此作出三个顶点平移后的对应点，再首尾顺次连接即可；
（2）分别作出三个顶点关于原点的对应点，再首尾顺次连接即可．
【详解】解：（1）如图所示；
（2）如图所示．
【点睛】本题主要考查作图—平移变换和旋转变换，解题的关键是掌握平移变换和旋转变换的定义与性质，并据此得出变换后的对应点．
17．见解析【分析】先根据直角三角形斜边上的中线性质得到OA＝OC＝OB，再根据旋转的性质得到OA＝OE，OC＝OF，∠AOC＝∠EOF，则OA＝OC＝OE＝OF，∠AOE＝∠COF，然后证明△AOE≌△COF，从而得到结论．
【详解】证明：∵∠BAC＝90°，点O为边BC的中点，
∴OA＝OC＝OB，
∵△AOC绕点O顺时针方向旋转，得到△EOF，
∴OA＝OE，OC＝OF，∠AOC＝∠EOF，
∴∠AOC＋∠COE＝∠EOF＋∠COE，OA＝OC＝OE＝OF，
即∠AOE＝∠COF，
在△AOE和△COF中，，
∴△AOE≌△COF（SAS），
∴AE＝CF．
【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了全等三角形的判定与性质，直角三角形斜边中线的性质．
18．(1)见解析
(2)，证明见解析
(3)能，
【分析】（1）由旋转的性质得出，．证明，由全等三角形的性质得出；
（2）延长到，使，交于点，证明，由全等三角形的性质得出，证明，由全等三角形的性质得出，则可得出结论；
（3）证出，若，则四边形是平行四边形，由全等三角形的性质及可列出关于的方程，求出即可得出答案．
（1）
解：证明：把绕点逆时针旋转得到线段，
，．
又，
，
在和中，
，
，
；
（2）
．
证明：延长到，使，交于点，
，，
，
，
，，
，
为的中点，
，
在的垂直平分线上，
又，
点在的垂直平分线上，
垂直平分，
，
在和中，
，
，
，
又，，
，
在和中，
，
，
，
又，
；
（3）
四边形能形成平行四边形．
，，
，
，
，
若，则四边形是平行四边形，
，
，
，
由（2）知，，
，
，
．
【点睛】本题是几何变换综合题，主要考查了等腰直角三角形的性质，旋转的性质，平行四边形的性质，全等三角形的判定与性质，勾股定理等知识，证明是解题的关键．
19．(1)见解析
(2)见解析
(3)
【分析】（１）首先利用矩形的性质可以得到，然后利用旋转的性质和等腰三角形的性质可以证明结论．
（２）连接HC，利用矩形的性质证明，然后利用全等三角形的性质证明四边形EHDC为平行四边形即可求解．
（３）过点O作于M，延长MO交AB于N，利用已知条件可以证明，接着证明四边形ADMN是矩形即可解决问题．
（1）
解：∵矩形ABCD
∴
∴
∵
∴
∴
∴ED平分
（2）
解：连接HC
∵矩形EFGC
∴
∴
∵，
∴
∴
∵
∴
∵
∴平行四边形EHDC
∴EC与DH互相平分
（3）
解：过点O作于M，延长MO交AB于N
∵， ，
∴
∴
∵，，
∴四边形ADMN是矩形
∴
∴
【点睛】本题考查了矩形的性质与判定，旋转的性质，等腰三角形的性质，全等三角形的性质，平行四边形的判定．
答案第1页，共2页