22.6反比例函数(一)课件
图片预览







文档简介
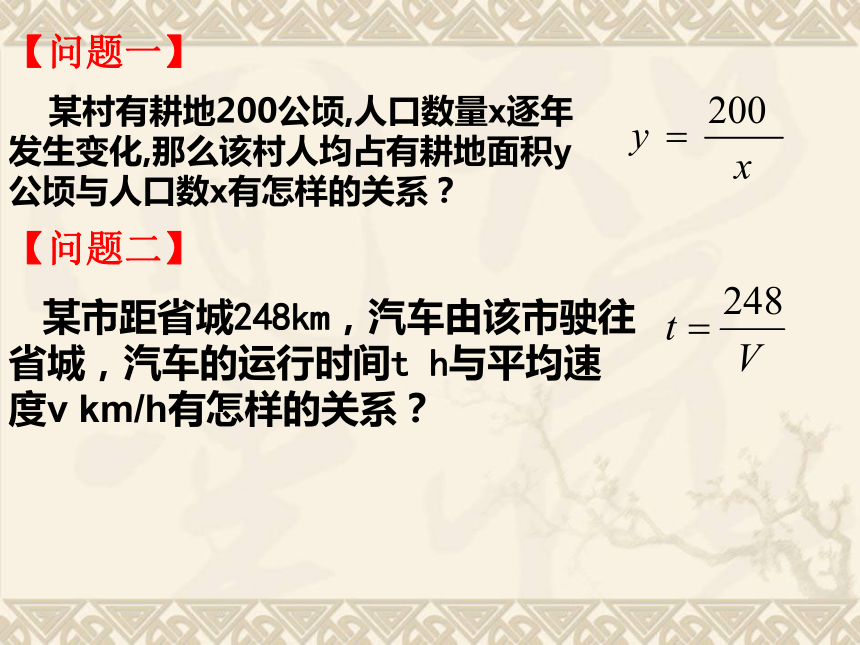
课件21张PPT。反比例函数(一) 1.什么叫函数? 在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.2.什么是一次函数?当b=0时, y=kx(k≠0)称y是x的正比例函数. 若两个变量 x、y之间的关系可以表示成y=kx+b(b为常数,k≠0)的形式,则称 y是x的一次函数 (x为自变量,y为因变量) .复习提问 3.回顾小学所学反比例关系。 两个相关联的量,一个量变化,另一个量也随着变化,如果两个数的积一定,这两个数的关系叫做反比例关系.复习提问 某村有耕地200公顷,人口数量x逐年发生变化,那么该村人均占有耕地面积y公顷与人口数x有怎样的关系?
【问题一】【问题二】 某市距省城248km,汽车由该市驶往省城,汽车的运行时间t h与平均速度v km/h有怎样的关系? 在下列实际问题中,变量间的对应关系可用怎样的函数关系式表示? (1)一辆以60km/h匀速行驶的汽车,它行驶的距离S(单位:km)随时间t(单位:h)的变化而变化。 ____________________ (2)一辆汽车的油箱中现有汽油50升,如果不再加油,平均每千米耗油量为0.1升,油箱中剩余的油量y(单位:升)随行驶里程 x(单位:千米)的变化而变化。 ______________________ (3)京沪线铁路全程为1463km,某次列车的平均速度v(单位:km/h)随此次列车的全程运行时间t(单位:h)的变化而变化。 _____________________函数关系式为:S=60t 函数关系式为:y=50-0.1x函数关系式为:生活情景(4)某住宅小区要种植一个面积为1000m2的矩形草坪,草坪的长y(单位:m )随宽x(单位:m )的变化而变化。 _____________________(5)已知北京市的总面积为1.68×104平方千米,人均占有的土地面积S(单位:平方千米/人)随全市总人口n(单位:人)的变化而变化。 ______________________(6)正方形的面积S随边长x的变化而变化。
____________________函数关系式为:函数关系式为:函数关系式为:S=x2生活情景S=60ty=50-0.1xS=x2在上面所列出函数中哪些是我们学过的函数?S=60t正比例函数y=kx (k为不等于零的常数)y=50- 0.1x一次函数y=kx+b (k≠0,k,b为常数) 在剩下的4个函数中,如果让你分为两类,你觉得应该怎么分?为什么?① ② ③ ④ ⑤ ⑥探求新知函数关系式:
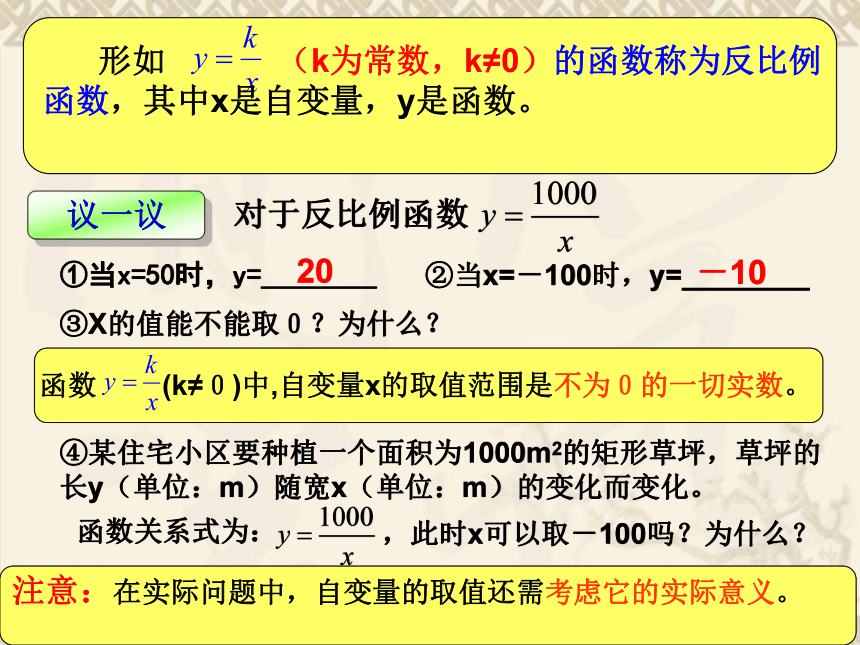
探求新知它们具有什么共同特征?具有 的形式,其中k≠0,k为常数.①当x=50时,y=________②当x=-100时,y=________20-10③X的值能不能取0?为什么? 形如 (k为常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数。1、写出下列问题中的函数关系式,并指出各是什么函数:⑴ 一个游泳池的容积为2000m3 ,注满游泳池所用的时间t(单位:h)随注水速度v(单位:m3 /h) 的变化而变化。⑵ 某长方体的体积为1000cm3 ,长方体的高(单位:cm)随底面积s(单位:cm2) 的变化而变化。⑶ 一个物体重100牛顿 ,物体对地面的压强p随物体与地面的接触面积s的变化而变化。步行课堂2、下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?步行课堂y是x的反比例函数,比例系数为k(k≠0)y=kx-1xy=k关系式xy+4=0中y是x的反比例函数吗?若是,比例系数k等于多少?若不是,请说明理由。-12、已知函数y=3xm-7是反比例函数,则 m = ___ . 6分析:即:m=1 3、当m取什么值时,函数 是x的反比例函数? 例1、已知y是x的反比例函数,当x=2时,y=6. (1)写出y与x的函数关系式; (2)求当x=4时y的值.,因为当 x=2 时y=6,所以有例题欣赏解得 k=12已知y是x的反比例函数,当x=3时,y=-8. 求当y=2时x的值.待定系数法求函数的解析式例2、y是x的反比例函数,下表给出了x与y的一些值:(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表.2-41例题欣赏魂牵梦绕待定系数法解:∵ y是x的反比例函数,2、已知y与x2 成反比例,并且当x=3时y=4.
⑴ 写出y和x之间的函数关系式;
⑵ 求x=2时y的值。漫步课外1、当m取什么值时,函数 是x的反比例函数?
3、已知函数 y = y1 + y2,y1与x 成正比例,y2与x成
反比例,且当x=1时,y=4;当x=2时,y=5。
(1)求y与x的函数关系式;
(2)当x=4时,y 的值。 方法:先分别设y1,y2与x的关系式,将两组值代入所设的函数关系式中,求出函数的值。解:(1)设 ,则∵x=1时,y=4;x=2时,y=5,∴y与x的函数关系式为(2)当x=4时,超越思维小 结反比例函数的意义:
若y是x的反比例函数,则 ;
若 ,则y是x的反比例函数。 二、方法一、知识点待定系数法做一做1、已知y 与 x 成反比例, 并且当 x = 3 时y = 7,求 x 与 y 的函数关式。变:若y与 x-2成反比例,又怎么设?4、已知点(2,5)在反比例函数 的图象上,其
中“■”是被污染的无法辨认的字迹,则下列各点在该反比例函数图象上的是( )
A (2,-5) B (-5,-2)
C (-3,4) D (4,-3)y=-3x+3B1.当m= 时,关于x的函数
y=(m+1)xm2-2是反比例函数?
分析:{m2-2=-1m+1≠0{即 m=±1m≠-11 2. 若 是关于 x的反比例函数,确定m的值,并求其函数关系式。
【问题一】【问题二】 某市距省城248km,汽车由该市驶往省城,汽车的运行时间t h与平均速度v km/h有怎样的关系? 在下列实际问题中,变量间的对应关系可用怎样的函数关系式表示? (1)一辆以60km/h匀速行驶的汽车,它行驶的距离S(单位:km)随时间t(单位:h)的变化而变化。 ____________________ (2)一辆汽车的油箱中现有汽油50升,如果不再加油,平均每千米耗油量为0.1升,油箱中剩余的油量y(单位:升)随行驶里程 x(单位:千米)的变化而变化。 ______________________ (3)京沪线铁路全程为1463km,某次列车的平均速度v(单位:km/h)随此次列车的全程运行时间t(单位:h)的变化而变化。 _____________________函数关系式为:S=60t 函数关系式为:y=50-0.1x函数关系式为:生活情景(4)某住宅小区要种植一个面积为1000m2的矩形草坪,草坪的长y(单位:m )随宽x(单位:m )的变化而变化。 _____________________(5)已知北京市的总面积为1.68×104平方千米,人均占有的土地面积S(单位:平方千米/人)随全市总人口n(单位:人)的变化而变化。 ______________________(6)正方形的面积S随边长x的变化而变化。
____________________函数关系式为:函数关系式为:函数关系式为:S=x2生活情景S=60ty=50-0.1xS=x2在上面所列出函数中哪些是我们学过的函数?S=60t正比例函数y=kx (k为不等于零的常数)y=50- 0.1x一次函数y=kx+b (k≠0,k,b为常数) 在剩下的4个函数中,如果让你分为两类,你觉得应该怎么分?为什么?① ② ③ ④ ⑤ ⑥探求新知函数关系式:
探求新知它们具有什么共同特征?具有 的形式,其中k≠0,k为常数.①当x=50时,y=________②当x=-100时,y=________20-10③X的值能不能取0?为什么? 形如 (k为常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数。1、写出下列问题中的函数关系式,并指出各是什么函数:⑴ 一个游泳池的容积为2000m3 ,注满游泳池所用的时间t(单位:h)随注水速度v(单位:m3 /h) 的变化而变化。⑵ 某长方体的体积为1000cm3 ,长方体的高(单位:cm)随底面积s(单位:cm2) 的变化而变化。⑶ 一个物体重100牛顿 ,物体对地面的压强p随物体与地面的接触面积s的变化而变化。步行课堂2、下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?步行课堂y是x的反比例函数,比例系数为k(k≠0)y=kx-1xy=k关系式xy+4=0中y是x的反比例函数吗?若是,比例系数k等于多少?若不是,请说明理由。-12、已知函数y=3xm-7是反比例函数,则 m = ___ . 6分析:即:m=1 3、当m取什么值时,函数 是x的反比例函数? 例1、已知y是x的反比例函数,当x=2时,y=6. (1)写出y与x的函数关系式; (2)求当x=4时y的值.,因为当 x=2 时y=6,所以有例题欣赏解得 k=12已知y是x的反比例函数,当x=3时,y=-8. 求当y=2时x的值.待定系数法求函数的解析式例2、y是x的反比例函数,下表给出了x与y的一些值:(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表.2-41例题欣赏魂牵梦绕待定系数法解:∵ y是x的反比例函数,2、已知y与x2 成反比例,并且当x=3时y=4.
⑴ 写出y和x之间的函数关系式;
⑵ 求x=2时y的值。漫步课外1、当m取什么值时,函数 是x的反比例函数?
3、已知函数 y = y1 + y2,y1与x 成正比例,y2与x成
反比例,且当x=1时,y=4;当x=2时,y=5。
(1)求y与x的函数关系式;
(2)当x=4时,y 的值。 方法:先分别设y1,y2与x的关系式,将两组值代入所设的函数关系式中,求出函数的值。解:(1)设 ,则∵x=1时,y=4;x=2时,y=5,∴y与x的函数关系式为(2)当x=4时,超越思维小 结反比例函数的意义:
若y是x的反比例函数,则 ;
若 ,则y是x的反比例函数。 二、方法一、知识点待定系数法做一做1、已知y 与 x 成反比例, 并且当 x = 3 时y = 7,求 x 与 y 的函数关式。变:若y与 x-2成反比例,又怎么设?4、已知点(2,5)在反比例函数 的图象上,其
中“■”是被污染的无法辨认的字迹,则下列各点在该反比例函数图象上的是( )
A (2,-5) B (-5,-2)
C (-3,4) D (4,-3)y=-3x+3B1.当m= 时,关于x的函数
y=(m+1)xm2-2是反比例函数?
分析:{m2-2=-1m+1≠0{即 m=±1m≠-11 2. 若 是关于 x的反比例函数,确定m的值,并求其函数关系式。
