2022-2023学年人教版(2012)八年级上册21.2解一元一次方程同步课时训练(word版含答案)
文档属性
| 名称 | 2022-2023学年人教版(2012)八年级上册21.2解一元一次方程同步课时训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 275.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 00:00:00 | ||
图片预览




文档简介
21.2 解一元一次方程 同步课时训练
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(每小题4分,共10各小题,共计40分)
1.代数式的值等于0,则x的值为( )
A.1 B.3 C. D.或1
2.一元二次方程的解是( )
A. B.
C. D.
3.对于实数m,n,定义一种运算☆为:.如果关于x的方程有两个相等的实数根,则a的值是( )
A. B.0 C.1 D.0或
4.若矩形的长和宽是方程4-12x+3=0的两个根,则该矩形的周长和面积分别为( )
A.3和 B.和3 C.和6 D.6和
5.关于x的一元二次方程的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的异号实数根
C.有两个不相等的同号实数根 D.没有实数根
6.已知关于x的一元二次方程的两根分别记为,若,则的值为( )
A.7 B. C.6 D.
7.用配方法解一元二次方程,下面配方正确的是( )
A. B. C. D.
8.在用配方法解方程时,可以将方程转化为其中所依据的一个数学公式是( )
A. B.
C. D.
9.用配方法解一元二次方程,下列配方正确的是( )
A. B. C. D.
10.若(x,y是实数),则M的值一定是( )
A.0 B.负数 C.正数 D.整数
评卷人得分
二、填空题(每小题5分,共5各小题,共计25分)
11.对于实数a,b,定义运算“◎”如下:.若(m+2)◎(m﹣3)=24,则m=_____.
12.若一元二次方程的一根为,则的值为______.
13.若关于x的方程有两个相等的实数根,则c的值为______.
14.把一元二次方程化成的形式,则的值为________.
15.已知是关于x的一元二次方程的两个实数根,则________.
评卷人得分
三、解答题(16、17、18题9分,19题8分,共计35分)
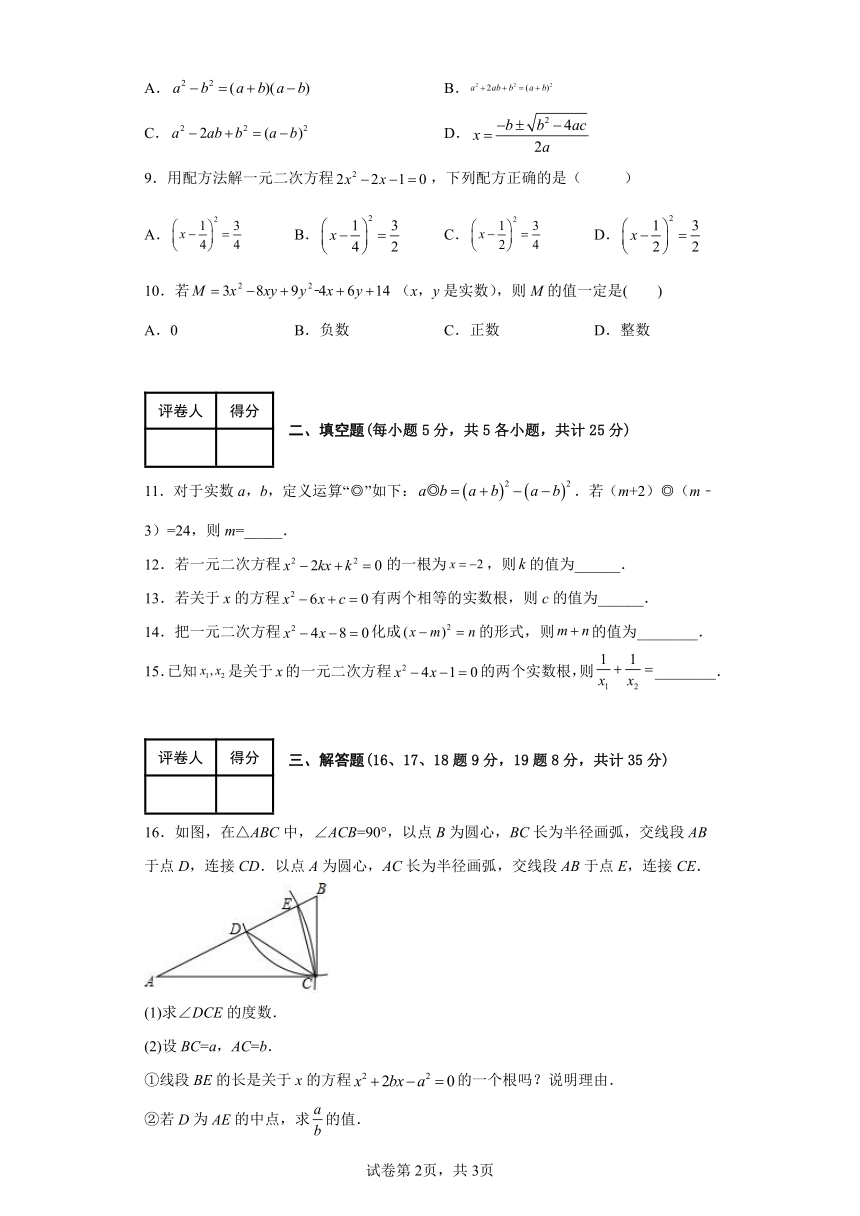
16.如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D,连接CD.以点A为圆心,AC长为半径画弧,交线段AB于点E,连接CE.
(1)求∠DCE的度数.
(2)设BC=a,AC=b.
①线段BE的长是关于x的方程的一个根吗?说明理由.
②若D为AE的中点,求的值.
17.(1)计算:;
(2)解方程:2﹣8=0.
18.关于的一元二次方程.
(1)若该方程有两个不相等的实数根,求的取值范围;
(2)若是该方程的两个实数根,且,求的值.
19.若x1、x2是关于x的一元二次方程kx-2x+4=0的两个实数根.
(1)求k的取值范围;
(2)若x1=,求(x1+1)(x2+1)的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A【分析】根据分式的值为零的条件即可求出答案.
【详解】解:由题意可知:,
解得:x=1,
故选:A.
【点睛】本题考查分式的值为零的条件,解题的关键是正确理解分式的值为零的条件,本题属于基础题型.
2.D【分析】利用配方法解方程即可.
【详解】解:∵,
∴,
∴,
∴,
∴,
解得,
故选D.
【点睛】本题主要考查了解一元二次方程,熟知解一元二次方程的方法是解题的关键.
3.B【分析】由于定义一种运算☆为:,关于x的方程有两个相等的实数根,所以根据判别式和一元二次方程的一般形式的定义可以得到关于a的关系式,即可解决问题.
【详解】解:由,
得,
依题意有,
∴,
解得,或a=-1(舍去).
故选:B.
【点睛】本题主要考查了一元二次方程的判别式,新定义,解题时首先正确理解定义的运算法则得到关于x的方程,然后根据判别式和一元二次方程的定义得到关系式解决问题.
4.D【分析】利用根与系数的关系求出两根之和与两根之积,即为长与宽的和与积,进而求出矩形周长与面积即可.
【详解】解:∵矩形的长和宽是方程4﹣12x+3=0的两个根,设长为a,宽为b,
∴a+b=3,ab,
则该矩形的周长为2(a+b)=6,面积为ab.
故选:D.
【点睛】此题考查了一元二次方程根与系数的关系,熟练掌握一元二次方程根与系数的关系是解本题的关键.
5.B【分析】先计算出根的判别式△的值,根据△的值就可以判断根的情况.
【详解】解:一元二次方程中,
∵△=,
∴原方程有两个不相等的实数根,
∵,
∴原方程有两个不相等的异号实数根.
故选:B.
【点睛】本题考查了根的判别式以及根与系数的关系,掌握一元二次方程根的情况与判别式△的关系是解题的关键,(1)△>0 方程有两个不相等的实数根;(2)△=0 方程有两个相等的实数根;(3)△<0 方程没有实数根.
6.B【分析】根据根与系数的关系求出,a的值,代入代数式求值即可.
【详解】解:将代入得,,解得:;
∴,
∴
∴,
故选:B.
【点睛】本题考查了根与系数的关系,掌握,是解题的关键.
7.A【分析】先化二次项系数为1,把常数项3右移,然后等式两边同时加上一次项系数 的一半的平方,再整理即可.
【详解】解:由原方程得, x=-3,
配方得: x+=-3+,即.
故选:A.
【点睛】本题考查解一元二次方程-配方法,配方法的一般步骤:(1)把常数项移到等号右边;(2)把二次项系数化为1;(3)等式两边同时加上一次项系数一半的平方,
8.B【分析】根据配方法解方程的基本步骤去判断依据即可.
【详解】用配方法解方程时,可以将方程转化为,
其中所依据的一个数学公式是.
故选:B.
【点睛】本题考查了配方法解方程的基本依据,熟练掌握配方的依据是完全平方公式是解题的依据.
9.C【分析】方程整理后,利用完全平方公式配方得到结果,即可作出判断.
【详解】解:方程2x2-2x-1=0,
整理得:x2-x=,
配方得:x2-x+=,即(x-)2=.
故选:C.
【点睛】此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.
10.C【分析】先将整式M进行变形为(x﹣2)2+(y+3)2+2(x﹣2y)2+1,然后根据二次方的非负性,即可得出答案.
【详解】解:M=3x2﹣8xy+9y2﹣4x+6y+14
=(x2﹣4x+4)+(y2+6y+9)+2(x2﹣4xy+4y2)+1
=(x﹣2)2+(y+3)2+2(x﹣2y)2+1
∵,,,
∴(x﹣2)2+(y+3)2+2(x﹣2y)2+1>0,故C正确.
故选:C.
【点睛】本题主要考查了配方法的应用和非负数的性质,将整式M变为(x﹣2)2+(y+3)2+2(x﹣2y)2+1,是解题的关键.
11.﹣3或4【分析】利用新定义得到 ,整理得到,然后利用因式分解法解方程.
【详解】解:根据题意得,
∴,
∴,
∴(2m﹣1+7)(2m﹣1﹣7)=0,
∴2m﹣1+7=0或2m﹣1﹣7=0,
解得m1=﹣3,m2=4.
故答案为:﹣3或4.
【点睛】本题主要考查了新定义下的实数运算,解一元二次方程,正确理解题意是解题的关键.
12.﹣2【分析】把x=﹣2代入方程计算即可求出k的值.
【详解】解:把x=﹣2代入方程得:4+4k+k2=0,
解得:k=﹣2,
故答案为:﹣2.
【点睛】此题考查一元二次方程的解及解法,方程的解即为能使方程左右两边相等的未知数的值,直接将方程的解代入,正确运算是解题的关键.
13.9【分析】根据一元二次方程根的判别式进行计算即可得到答案.
【详解】解:△=(-6)2-4c=0,解得c=9,
故答案为9.
【点睛】本题考查一元二次方程根的判别式,根据根的情况列出方程是解题的关键.
14.14【分析】将一元二次方程进行配方,即可对应得到m和n的值.
【详解】解:,即,
∴,即,
∴,,
∴,
故答案为:14.
【点睛】本题考查配方法,利用完全平方公式对方程进行配方时,注意运算准确.
15.【分析】利用根与系数的关系求出x1+x2与x1x2,原式通分并利用同分母分式的加法法则计算,将各自的值代入计算即可求出值.
【详解】解:∵x1,x2是关于x的一元二次方程x2-4x-1=0的两个实数根,
∴x1+x2=4,x1 x2=-1,
则原式4.
故答案为:-4.
【点睛】本题考查了一元二次方程根与系数的关系,熟练掌握根与系数的关系是解题的关键.
16.(1)45°
(2)①线段BE的长是关于x的方程x2+2bx﹣a2=0的一个根,详见解析;②
【分析】(1)利用等腰三角形的性质结合三角形内角和定理得出答案;
(2)①直接利用勾股定理得出AB的长,再利用配方法解方程得出答案;②直接利用勾股定理得出等式求出答案.
(1)
解:∵BC=BD,
∴∠BCD=∠BDC,
∵AC=AE,
∴∠ACE=∠AEC,
∵∠ACB=90°,
∴∠BCD+∠ACE﹣∠DCE=90°,
又∵在△DCE中,∠BDC+∠AEC+∠DCE=180°,
∴90°+2∠DCE=180°,
∴∠DCE=45°.
(2)
解:①线段BE的长是关于x的方程的一个根.理由如下:
由勾股定理得:,
∴,
∵,
∴,
∴
解得,
∴线段BE的长是关于x的方程的一个根;
②∵D为AE的中点,
∴,
由勾股定理得: ,
∴,
∴,
∴,
∵,
∴.
【点睛】本题主要考查了三角形内角和定理,等腰三角形的性质,勾股定理,解一元二次方程,熟知相关知识是解题的关键.
17.(1);(2)【分析】(1)直接利用二次根式的加减运算求解即可;
(2)直接利用开方法解方程即可.
【详解】解:(1)原式
;
(2),
,
∴,
∴,.
【点睛】题目主要考查二次根式的加减运算及运用开方法解方程,熟练掌握运算方法是解题关键.
18.(1)m的取值范围是m<0;
(2)m的值是-2.
【分析】(1)由一元二次方程的根的情况与判别式的关系可得Δ>0,由此可解得m的值;
(2)根与系数的关系及已知条件可得关于m的一元二次方程,解得m的值并根据(1)中的所得的m的取值范围作出取舍即可得出答案.
(1)
解:根据题意得:
Δ= >0,
解得:m<0.
∴m的取值范围是m<0;
(2)
解:根据题意得:,,
∵,
∴,
∴,
∴解得:,(不合题意,舍去),
∴m的值是-2.
【点睛】本题考查了一元二次方程的根的情况与判别式的关系、及根与系数的关系及解一元二次方程等知识点,熟练掌握一元二次方程的相关知识是解题的关键.
19.(1)且
(2)
【分析】(1)方程有两个实数根,结合根的判别式即可得出关于k的一元一次不等式,结合即可得出k的取值范围;
(2)将x1=代入方程求出k的值,利用根与系数的关系即可得出x1+x2=,x1x2=,代入(x1+1)(x2+1)即可求解.
(1)
解:∵关于x的一元二次方程kx-2x+4=0有两个实数根,
∴,
∴,
∵kx-2x+4=0是一元二次方程,
∴,
∴且;
(2)
解:将x1=代入方程kx-2x+4=0得,
解得,
∴,
由根与系数的关系,得:x1+x2=,x1x2=,
∴(x1+1)(x2+1) .
【点睛】本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)根据方程有两个实数根得出;(2)根据根与系数的关系求出x1+x2和x1x2的值.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(每小题4分,共10各小题,共计40分)
1.代数式的值等于0,则x的值为( )
A.1 B.3 C. D.或1
2.一元二次方程的解是( )
A. B.
C. D.
3.对于实数m,n,定义一种运算☆为:.如果关于x的方程有两个相等的实数根,则a的值是( )
A. B.0 C.1 D.0或
4.若矩形的长和宽是方程4-12x+3=0的两个根,则该矩形的周长和面积分别为( )
A.3和 B.和3 C.和6 D.6和
5.关于x的一元二次方程的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的异号实数根
C.有两个不相等的同号实数根 D.没有实数根
6.已知关于x的一元二次方程的两根分别记为,若,则的值为( )
A.7 B. C.6 D.
7.用配方法解一元二次方程,下面配方正确的是( )
A. B. C. D.
8.在用配方法解方程时,可以将方程转化为其中所依据的一个数学公式是( )
A. B.
C. D.
9.用配方法解一元二次方程,下列配方正确的是( )
A. B. C. D.
10.若(x,y是实数),则M的值一定是( )
A.0 B.负数 C.正数 D.整数
评卷人得分
二、填空题(每小题5分,共5各小题,共计25分)
11.对于实数a,b,定义运算“◎”如下:.若(m+2)◎(m﹣3)=24,则m=_____.
12.若一元二次方程的一根为,则的值为______.
13.若关于x的方程有两个相等的实数根,则c的值为______.
14.把一元二次方程化成的形式,则的值为________.
15.已知是关于x的一元二次方程的两个实数根,则________.
评卷人得分
三、解答题(16、17、18题9分,19题8分,共计35分)
16.如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D,连接CD.以点A为圆心,AC长为半径画弧,交线段AB于点E,连接CE.
(1)求∠DCE的度数.
(2)设BC=a,AC=b.
①线段BE的长是关于x的方程的一个根吗?说明理由.
②若D为AE的中点,求的值.
17.(1)计算:;
(2)解方程:2﹣8=0.
18.关于的一元二次方程.
(1)若该方程有两个不相等的实数根,求的取值范围;
(2)若是该方程的两个实数根,且,求的值.
19.若x1、x2是关于x的一元二次方程kx-2x+4=0的两个实数根.
(1)求k的取值范围;
(2)若x1=,求(x1+1)(x2+1)的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A【分析】根据分式的值为零的条件即可求出答案.
【详解】解:由题意可知:,
解得:x=1,
故选:A.
【点睛】本题考查分式的值为零的条件,解题的关键是正确理解分式的值为零的条件,本题属于基础题型.
2.D【分析】利用配方法解方程即可.
【详解】解:∵,
∴,
∴,
∴,
∴,
解得,
故选D.
【点睛】本题主要考查了解一元二次方程,熟知解一元二次方程的方法是解题的关键.
3.B【分析】由于定义一种运算☆为:,关于x的方程有两个相等的实数根,所以根据判别式和一元二次方程的一般形式的定义可以得到关于a的关系式,即可解决问题.
【详解】解:由,
得,
依题意有,
∴,
解得,或a=-1(舍去).
故选:B.
【点睛】本题主要考查了一元二次方程的判别式,新定义,解题时首先正确理解定义的运算法则得到关于x的方程,然后根据判别式和一元二次方程的定义得到关系式解决问题.
4.D【分析】利用根与系数的关系求出两根之和与两根之积,即为长与宽的和与积,进而求出矩形周长与面积即可.
【详解】解:∵矩形的长和宽是方程4﹣12x+3=0的两个根,设长为a,宽为b,
∴a+b=3,ab,
则该矩形的周长为2(a+b)=6,面积为ab.
故选:D.
【点睛】此题考查了一元二次方程根与系数的关系,熟练掌握一元二次方程根与系数的关系是解本题的关键.
5.B【分析】先计算出根的判别式△的值,根据△的值就可以判断根的情况.
【详解】解:一元二次方程中,
∵△=,
∴原方程有两个不相等的实数根,
∵,
∴原方程有两个不相等的异号实数根.
故选:B.
【点睛】本题考查了根的判别式以及根与系数的关系,掌握一元二次方程根的情况与判别式△的关系是解题的关键,(1)△>0 方程有两个不相等的实数根;(2)△=0 方程有两个相等的实数根;(3)△<0 方程没有实数根.
6.B【分析】根据根与系数的关系求出,a的值,代入代数式求值即可.
【详解】解:将代入得,,解得:;
∴,
∴
∴,
故选:B.
【点睛】本题考查了根与系数的关系,掌握,是解题的关键.
7.A【分析】先化二次项系数为1,把常数项3右移,然后等式两边同时加上一次项系数 的一半的平方,再整理即可.
【详解】解:由原方程得, x=-3,
配方得: x+=-3+,即.
故选:A.
【点睛】本题考查解一元二次方程-配方法,配方法的一般步骤:(1)把常数项移到等号右边;(2)把二次项系数化为1;(3)等式两边同时加上一次项系数一半的平方,
8.B【分析】根据配方法解方程的基本步骤去判断依据即可.
【详解】用配方法解方程时,可以将方程转化为,
其中所依据的一个数学公式是.
故选:B.
【点睛】本题考查了配方法解方程的基本依据,熟练掌握配方的依据是完全平方公式是解题的依据.
9.C【分析】方程整理后,利用完全平方公式配方得到结果,即可作出判断.
【详解】解:方程2x2-2x-1=0,
整理得:x2-x=,
配方得:x2-x+=,即(x-)2=.
故选:C.
【点睛】此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.
10.C【分析】先将整式M进行变形为(x﹣2)2+(y+3)2+2(x﹣2y)2+1,然后根据二次方的非负性,即可得出答案.
【详解】解:M=3x2﹣8xy+9y2﹣4x+6y+14
=(x2﹣4x+4)+(y2+6y+9)+2(x2﹣4xy+4y2)+1
=(x﹣2)2+(y+3)2+2(x﹣2y)2+1
∵,,,
∴(x﹣2)2+(y+3)2+2(x﹣2y)2+1>0,故C正确.
故选:C.
【点睛】本题主要考查了配方法的应用和非负数的性质,将整式M变为(x﹣2)2+(y+3)2+2(x﹣2y)2+1,是解题的关键.
11.﹣3或4【分析】利用新定义得到 ,整理得到,然后利用因式分解法解方程.
【详解】解:根据题意得,
∴,
∴,
∴(2m﹣1+7)(2m﹣1﹣7)=0,
∴2m﹣1+7=0或2m﹣1﹣7=0,
解得m1=﹣3,m2=4.
故答案为:﹣3或4.
【点睛】本题主要考查了新定义下的实数运算,解一元二次方程,正确理解题意是解题的关键.
12.﹣2【分析】把x=﹣2代入方程计算即可求出k的值.
【详解】解:把x=﹣2代入方程得:4+4k+k2=0,
解得:k=﹣2,
故答案为:﹣2.
【点睛】此题考查一元二次方程的解及解法,方程的解即为能使方程左右两边相等的未知数的值,直接将方程的解代入,正确运算是解题的关键.
13.9【分析】根据一元二次方程根的判别式进行计算即可得到答案.
【详解】解:△=(-6)2-4c=0,解得c=9,
故答案为9.
【点睛】本题考查一元二次方程根的判别式,根据根的情况列出方程是解题的关键.
14.14【分析】将一元二次方程进行配方,即可对应得到m和n的值.
【详解】解:,即,
∴,即,
∴,,
∴,
故答案为:14.
【点睛】本题考查配方法,利用完全平方公式对方程进行配方时,注意运算准确.
15.【分析】利用根与系数的关系求出x1+x2与x1x2,原式通分并利用同分母分式的加法法则计算,将各自的值代入计算即可求出值.
【详解】解:∵x1,x2是关于x的一元二次方程x2-4x-1=0的两个实数根,
∴x1+x2=4,x1 x2=-1,
则原式4.
故答案为:-4.
【点睛】本题考查了一元二次方程根与系数的关系,熟练掌握根与系数的关系是解题的关键.
16.(1)45°
(2)①线段BE的长是关于x的方程x2+2bx﹣a2=0的一个根,详见解析;②
【分析】(1)利用等腰三角形的性质结合三角形内角和定理得出答案;
(2)①直接利用勾股定理得出AB的长,再利用配方法解方程得出答案;②直接利用勾股定理得出等式求出答案.
(1)
解:∵BC=BD,
∴∠BCD=∠BDC,
∵AC=AE,
∴∠ACE=∠AEC,
∵∠ACB=90°,
∴∠BCD+∠ACE﹣∠DCE=90°,
又∵在△DCE中,∠BDC+∠AEC+∠DCE=180°,
∴90°+2∠DCE=180°,
∴∠DCE=45°.
(2)
解:①线段BE的长是关于x的方程的一个根.理由如下:
由勾股定理得:,
∴,
∵,
∴,
∴
解得,
∴线段BE的长是关于x的方程的一个根;
②∵D为AE的中点,
∴,
由勾股定理得: ,
∴,
∴,
∴,
∵,
∴.
【点睛】本题主要考查了三角形内角和定理,等腰三角形的性质,勾股定理,解一元二次方程,熟知相关知识是解题的关键.
17.(1);(2)【分析】(1)直接利用二次根式的加减运算求解即可;
(2)直接利用开方法解方程即可.
【详解】解:(1)原式
;
(2),
,
∴,
∴,.
【点睛】题目主要考查二次根式的加减运算及运用开方法解方程,熟练掌握运算方法是解题关键.
18.(1)m的取值范围是m<0;
(2)m的值是-2.
【分析】(1)由一元二次方程的根的情况与判别式的关系可得Δ>0,由此可解得m的值;
(2)根与系数的关系及已知条件可得关于m的一元二次方程,解得m的值并根据(1)中的所得的m的取值范围作出取舍即可得出答案.
(1)
解:根据题意得:
Δ= >0,
解得:m<0.
∴m的取值范围是m<0;
(2)
解:根据题意得:,,
∵,
∴,
∴,
∴解得:,(不合题意,舍去),
∴m的值是-2.
【点睛】本题考查了一元二次方程的根的情况与判别式的关系、及根与系数的关系及解一元二次方程等知识点,熟练掌握一元二次方程的相关知识是解题的关键.
19.(1)且
(2)
【分析】(1)方程有两个实数根,结合根的判别式即可得出关于k的一元一次不等式,结合即可得出k的取值范围;
(2)将x1=代入方程求出k的值,利用根与系数的关系即可得出x1+x2=,x1x2=,代入(x1+1)(x2+1)即可求解.
(1)
解:∵关于x的一元二次方程kx-2x+4=0有两个实数根,
∴,
∴,
∵kx-2x+4=0是一元二次方程,
∴,
∴且;
(2)
解:将x1=代入方程kx-2x+4=0得,
解得,
∴,
由根与系数的关系,得:x1+x2=,x1x2=,
∴(x1+1)(x2+1) .
【点睛】本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)根据方程有两个实数根得出;(2)根据根与系数的关系求出x1+x2和x1x2的值.
答案第1页,共2页
答案第1页,共2页
同课章节目录
