2022-2023学年人教版(2012)八年级上册24.1圆的有关性质同步课时训练(word版含答案)
文档属性
| 名称 | 2022-2023学年人教版(2012)八年级上册24.1圆的有关性质同步课时训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 778.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 09:17:24 | ||
图片预览

文档简介
24.1 圆的有关性质 同步课时训练
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(每小题4分,共10各小题,共计40分)
1.如图所示,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是()
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.
2.如图,的弦垂直于,为垂足,,,且,则圆心到的距离是( )
A.2 B. C. D.
3.如图,四边形ABCD内接于⊙O,若,则∠BCD的度数是( )
A.50° B.80° C.100° D.130°
4.如图,AB为⊙O的直径,半径OA的垂直平分线交⊙O于点C,D,P为优弧ABC上一点,则∠APC=( )
A.20° B.30° C.35° D.40°
5.如图,已知AB为⊙O的直径,点C在⊙O上,∠A=15°,则∠BOC的度数为( )
A.15° B.30° C.45° D.60°
6.如图,内接于,,D是边BC的中点,连接OD并延长,交于点E,则的大小为( )
A. B. C. D.
7.如图,在⊙O中,所对的圆周角∠ACB=70°,若P为一点,∠AOP=75°,则∠POB的度数为( )
A.50° B.65° C.75° D.80°
8.如图,是的直径,是上一点,若,则的度数是( )
A. B. C. D.
9.如图,点A,B,C是⊙O上的三点,若,,则∠AOB的大小为( )
A.25° B.30° C.35° D.40°
10.如图,在RtABC中,∠CAB=36°,斜边AC与量角器的直径重合(A点的刻度为0),将射线BF绕着点B转动,与量角器的外圆弧交于点D,与AC交于点E,若ABE是等腰三角形,则点D在量角器上对应的刻度为( )
A.72° B.144° C.36°或72° D.72°或144°
评卷人得分
二、填空题(每小题5分,共5各小题,共计25分)
11.如图,在中,弦半径,则的度数为____________.
12.如图正方形的边长为1,分别以正方形的两个相对顶点为圆心,以1为半径画弧,则图中阴影部分的面积是______(用含有的式子表示).
13.如图,⊙O的半径为2,弦AB=,点C是弦AB上一动点,OC长为整数,则OC的长为______.
14.把一个球放入长方体纸盒,球的一部分露出盒外,球与纸盒内壁都刚好相切,其截面如图所示,若露出部分的高度为6cm,AF=DE=3cm,则这个球的半径是_____cm.
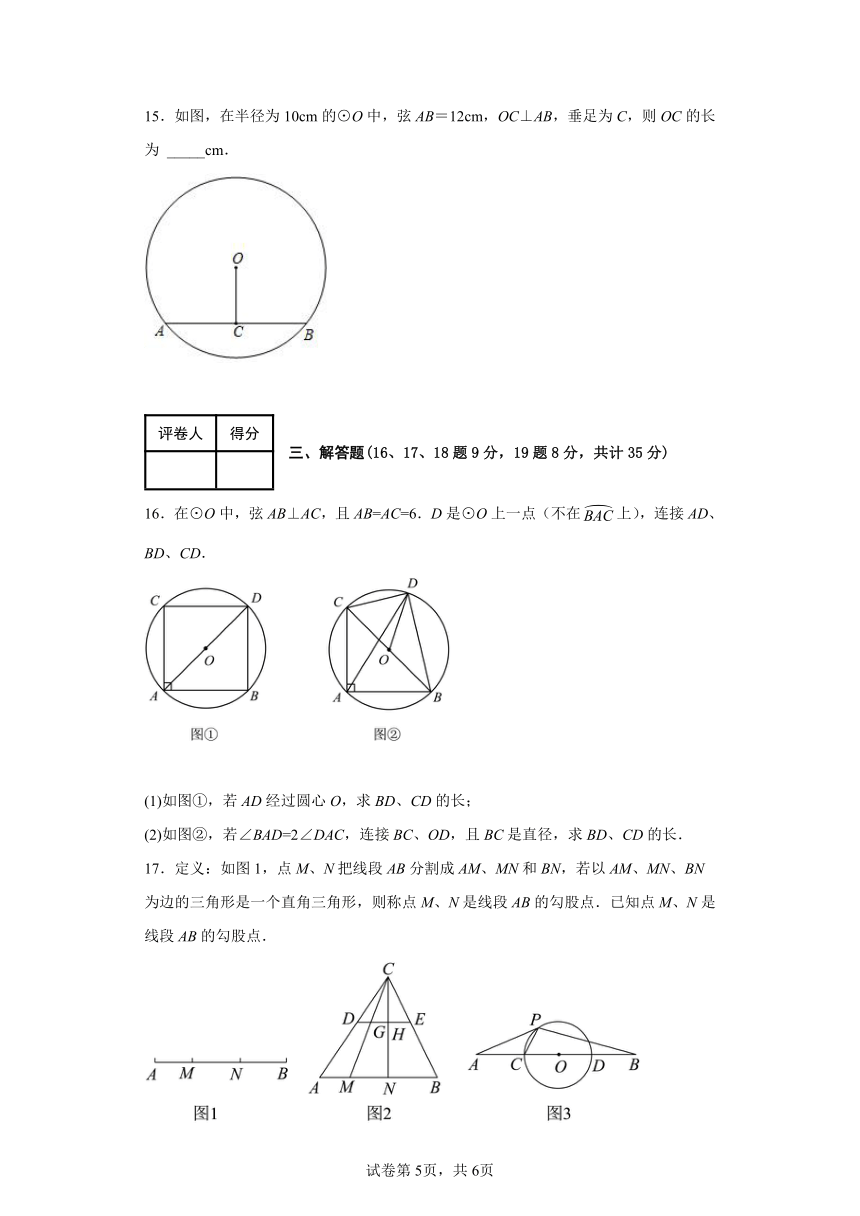
15.如图,在半径为10cm的⊙O中,弦AB=12cm,OC⊥AB,垂足为C,则OC的长为 _____cm.
评卷人得分
三、解答题(16、17、18题9分,19题8分,共计35分)
16.在⊙O中,弦AB⊥AC,且AB=AC=6.D是⊙O上一点(不在上),连接AD、BD、CD.
(1)如图①,若AD经过圆心O,求BD、CD的长;
(2)如图②,若∠BAD=2∠DAC,连接BC、OD,且BC是直径,求BD、CD的长.
17.定义:如图1,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股点.已知点M、N是线段AB的勾股点.
(1)若AM=1,MN=2,则BN= ;
(2)如图2,DE是△ABC的中位线,M、N是AB边的勾股点(AM<MN<NB),连接CM、CN分别交DE于点G、H.求证:G、H是线段DE的勾股点.
(3)如图3,C,D是线段AB的勾股点(AC18.如图,四边形内接于,为的直径,平分,点E在的延长线上,连接.
(1)求直径的长;
(2)若,计算图中阴影部分的面积.
19.如图,点A、B、C在⊙O上, AB=CB=9, AD∥BC,CD⊥AD,且AD=2.
(1)求线段CD、AC的长;
(2)求⊙O的半径.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C【分析】根据垂径定理可得:,DE=CE,进而得到∠COE=∠DOE,无法得到OE=BE.
【详解】∵AB是⊙O的直径,CD为弦,CD⊥AB于点E,
∴,DE=CE,,
∴B,D选项正确;
∵,
∴,
∴∠COE=∠DOE,
∴A选项正确;
只有当∠COE=60°时,才有OE=BE.
∴C选项不成立;
故选:C.
【点睛】本题考查了垂径定理和圆心角、弧之间的关系.解题的关键是熟练掌握垂径定理.垂径定理:垂直弦的直径平分弦,并且平分弦所对的弧.
2.A【分析】连接,过点,分别作与,于,则四边形是矩形,证明,可得,根据垂径定理可得,根据即可求解.
【详解】连接,过点,分别作于,于,则四边形是矩形,
,,
,
,
,
(HL),
,
则,
,
,
,
.
故选:A.
【点睛】本题考查了垂径定理,掌握垂径定理是解题的关键.
3.D【分析】根据圆周角定理求出∠A的度数,根据圆内接四边形的性质得出∠A+∠BCD=180°即可解答.
【详解】解:∵弧BCD对的圆周角是∠A,圆心角是∠BOD=100°,
∴∠A=∠BOD=50°,
∵A、B、C、D四点共圆,
∴∠A+∠BCD=180°,
∴∠BCD=130°.
故选:D.
【点睛】本题主要考查了圆周角定理、圆内接四边形的性质等知识点,根据圆周角定理求得∠A的度数和得出∠A+∠BCD=180°是解答本题的关键.
4.B【分析】连接OC,设DC与OA的交点为E,则OE=,求得∠OCE=30°,∠AOC=60°,根据圆周角定理计算即可.
【详解】如图,连接OC,设DC与OA的交点为E,
根据题意,AB为⊙O的直径,半径OA的垂直平分线交⊙O于点C,D,
得OE=,
∴∠OCE=30°,∠AOC=60°,
∴∠APC==30°,
故选B.
【点睛】本题考查了垂径定理,圆周角定理,勾股定理,直角三角形的性质,熟练掌握垂径定理,圆周角定理是解题的关键.
5.B【分析】根据圆周角定理解答.
【详解】解:∠BOC=2∠BAC=2×15°=30°,
故选:B.
【点睛】本题考查了圆周角定理,要知道,同弧所对的圆周角是它所对圆心角的一半.
6.C【分析】连接CE,根据圆内接四边形的性质得到∠BEC=180°﹣∠A=140°,根据垂径定理得到OE⊥BC,求得BD=CD,根据等腰三角形的性质即可得到结论.
【详解】解:如下图,连接CD,
∵∠A=40°,
∴∠BEC=180°﹣∠A=140°,
∵D是边BC的中点,
∴OE⊥BC,BD=CD,
∴BE=CE,
∴.
故选:C.
【点睛】本题考查了圆内接四边形的性质、垂径定理、等腰三角形的性质等知识,正确理解题意是解题的关键.
7.B【分析】先利用圆周角定理得到∠AOB=2∠ACB=140°,然后根据角的和差求解即可.
【详解】解:∵所对的圆周角∠ACB=70°,
∴∠AOB=2∠ACB=2×70°=140°,
∵∠AOP=75°,
∴∠POB=∠AOB-∠AOP=140°-75°=65°.
故选:B.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
8.B【分析】根据直径所对的圆周角是直角,直角三角形的两个锐角互余计算判断即可.
【详解】∵ 是的直径,
∴
∵ ,
∴=58°,
故选B.
【点睛】本题考查了圆周角定理,直角三角形的性质,熟练掌握圆周角定理是解题的关键.
9.A【分析】根据“同弧所对的圆周角是圆心角的一半”可求出,由图可知∠AOB=,即可求解.
【详解】∵,
∴,
∵,
∴∠AOB==85°-60°=25°,
故选:A
【点睛】本题主要考查了圆心角和圆周角,熟练地掌握“同弧所对的圆周角是圆心角的一半”是解题的关键.
10.D【分析】如图,点O是AC中点,连接DO,易知点D在量角器上对应的度数=∠AOD=-∠DOC=2∠DBC,只要求出∠DBC的度数即可解决问题.
【详解】解:如图,点O是AB中点,连接DO,
点D在量角器上对应的度数=∠AOD=-∠DOC=-2∠DBC,
∵ABE是等腰三角形,
当为顶角时,
,
,
∠DOC=2∠DBC=,
∴点D在量角器上对应的度数=;
当为底角时,
,
,
∠DOC=2∠DBC=,
点D在量角器上对应的度数=.
故选:D.
【点睛】本题考查圆心角与圆周角的关系,量角器、等腰三角形的判定和性质等知识,解题的关键是理解∠COD=2∠CBD,学会分类讨论的思想.
11.100°##100度【分析】先根据平行线的性质求出∠OCA的度数,再根据等边对等角求出∠OAC的度数,即可利用三角形内角和定理求出∠AOC的度数.
【详解】解:∵,
∴∠OCA=∠BOC=40°,
∵OA=OC,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°-∠OAC-∠OCA=100°,
故答案为:100°.
【点睛】本题主要考查了平行线的性质,圆的基本性质,三角形内角和定理,等腰三角形的性质,熟知相关知识是解题的关键.
12.【分析】利用两个圆的面积减去一个正方形的面积求解即可.
【详解】解:如图所示
S阴影=-S正方形=-12=.
故答案为:.
【点睛】本题考查阴影面积的求解,利用S阴影=-S正方形进行求解是解决本题的关键.
13.1或2【分析】作OH⊥AB于H,根据垂径定理得AH=BH=AB=,再在Rt△BOH中,根据勾股定理得OH=1,再求出OC的取值范围,最后可得答案.
【详解】解:作OH⊥AB于H,如图,
∵OH⊥AB,
∴AH=BH,
∴AH=BH=AB=×=,
在Rt△BOH中,OB=2,BH=,
∴OH=,
∵点C是弦AB上一动点,
∴
∵OC长为整数,
∴OC=1或2,
故答案为:1或2
【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
14.15【分析】过作于,交于,连接,设半径为,根据勾股定理列方程即可得到结论.
【详解】解:过作于,交于,连接,
,
,
设半径为,则,,,
根据勾股定理得,,
解得:或3(舍,
答:这个球的半径为.
故答案为:15.
【点睛】本题考查了垂径定理及勾股定理的知识,解题的关键是正确的作出辅助线构造直角三角形.
15.8【分析】根据“垂径定理”即可得出AC的长度,连接AO,构建直角三角形,用勾股定理即可求出OC.
【详解】连接AO,
∵OC⊥AB,且AB=12cm,
∴AC=6cm
∵半径为10cm
∴AO=10cm
在Rt△AOC中,由勾股定理可得:OC=cm
故答案为:8
【点睛】本题主要考查了“垂径定理”的运用,垂直于直径的弦被直径平分.熟练地掌握垂径定理并能够根据题意构建直角三角形是解题的关键.
16.(1)BD=6,CD=6
(2),BD=
【分析】(1)由AD经过圆心O,利用圆周角定理得∠ACD=∠ABD=90°,又因为AB⊥AC,得到四边形ABCD为矩形,易得结果;
(2)由∠BAD=2∠DAC,AB⊥AC,由圆周角定理得BC为直径,易得∠CAD=30°,∠BAD=60°,证明△COD为等边三角形,求得CD,BD.
(1)
解:AD是⊙O的直径,
∴∠C=∠B=90°,
∵AB⊥AC,
∴∠BAC=90°,
∴四边形ABDC是矩形,
∵AB=AC=6,
∴BD=AC=6,CD=AB=6;
(2)
∵∠BAC=90°,∠BAD=2∠DAC,
∴∠BAD=60°,∠DAC=30°,
∴∠COD=2∠CAD=60°,
∵OC=OD,
∴△COD是等边三角形,
∴CD=OC,
在Rt△ABC中,,
∴,
在Rt△BCD中,.
【点睛】本题主要考查了圆周角定理、勾股定理、等边三角形的判定和性质、矩形的判定和性质等知识,熟练掌握相关定理是解答此题的关键.
17.(1)或
(2)见解析
(3)
【分析】(1)根据题意分两类进行讨论,并由勾股定理求解即可.
(2)根据DE是△ABC的中位线,可得,并且分别为各边的中点,然后得到分别为中位线,最后根据题意列出关系式,即可得证.
(3)连接PD,由题意可得,根据圆周角定理可知∠CPD=90°,再由勾股定理,得到以及各角间的关系,从而求出的度数,进而得到结论.
(1)
解:∵点M、N是线段AB的勾股点,
∴或
∴BN的长为;
故答案为:;
(2)
证明:如图2,
∵DE是△ABC的中位线,
∴DE∥AB,CD=AD,CE=BE,
∴CG=GM,CH=HN,
∴DG=AM,GH=MN,EH=BN,
∵M、N是AB边的勾股点(AM<MN<NB),
∴BN2=MN2+AM2,
∴BN2=MN2+AM2,
∴(BN)2=(MN)2+(AM)2,
∴EH2=GH2+DG2,
∴G、H是线段DE的勾股点;
(3)
解:如图3,连接PD,
∵AC=PC,
∴∠A=∠APC,
∴∠PCD=2∠A,
∵C,D是线段AB的勾股点,
∴AC2+BD2=CD2,
∴PC2+BD2=CD2,
∵CD是⊙O的直径,
∴∠CPD=90°,
∴PC2+PD2=CD2,
∴PD=BD,
∴∠PDC=2∠B,
∵∠A=2∠B,
∴∠PDC=∠A,
在Rt△PCD中,∵∠PCD+∠PDC=90°,
∴2∠A+∠A=90°,
∴∠A=30°,
∴∠B=∠A=15°.
【点睛】此题主要考查了圆的有关知识、勾股定理以及新定义勾股点的理解和运用,解题关键是对新定义的理解与运用.
18.(1)4
(2)6
【分析】(1)设辅助线,利用直径、角平分线的性质得出的度数,利用圆周角与圆心角的关系得出的度数,根据半径与直径的关系,结合勾股定理即可得出结论.
(2)由(1)已知,得出的度数,根据圆周角的性质结合得出,再根据直径、等腰直角三角形的性质得出的值,进而利用直角三角形面积公式求出,由阴影部分面积可知即为所求.
(1)解:如图所示,连接,为的直径,平分,,,..,,,即...
(2)解:如图所示,设其中小阴影面积为,大阴影面积为,弦与劣弧所形成的面积为,由(1)已知,,,,.,弦弦,劣弧劣弧..为的直径,,,.,...
【点睛】本题考查圆的性质的理解与综合应用能力.涉及对半径与直径的关系,直径的性质,圆周角与圆心角的关系,圆周角的性质,勾股定理,直角三角形,角平分线等知识点.半径等于直径的一半;直径所对的圆周角是直角;在同圆或等圆中,相等的弦所对的圆周角等于圆心角的一半;在同圆或等圆中,圆周角相等弧相等弦相等.一个直角三角中,两个直角边边长的平方加起来等于斜边长的平方.恰当借助辅助线,灵活运用圆周角的性质建立等式关系是解本题的关键.
19.(1)CD=;AC=6
(2)
【分析】(1)作AE⊥BC于E,易证四边形AECD为矩形,可得EC=AD=2,BE=BC EC=7,再利用勾股定理求解即可;
(2)连接AO并延长交⊙O于点F,连接BF,证明△ABF∽△CDA,利用相似三角形的性质求出AF即可.
(1)解:作AE⊥BC,垂足为E,∵AD∥BC,∴AE⊥AD,∵CD⊥AD,∴四边形AECD为矩形,∴EC=AD=2,∴BE=9-2=7,∴在Rt△AEB中,AE2=AB2-BE2=32,在Rt△AEC中,AC2=AE2+CE2=36,∴AC=6,在Rt△ACD中,CD=;
(2)连接AO并延长交⊙O于点F,连接BF,∴∠F=∠ACB,∵AD∥BC,∴∠DAC=∠ACB,∴∠F=∠DAC,∵AF为⊙O的直径,∴∠ABF=90°,∴∠ADC=∠ABF=90°, ∴△ABF∽△CDA,∴,∵四边形AECD为矩形,∴CD=AE=,∴,∴AF=,∴⊙O的半径r=.
【点睛】本题考查了矩形的判定和性质,勾股定理,平行线的性质,圆周角定理,相似三角形的判定和性质等知识,作出合适的辅助线构造出直角三角形和相似三角形是解题的关键.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(每小题4分,共10各小题,共计40分)
1.如图所示,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是()
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.
2.如图,的弦垂直于,为垂足,,,且,则圆心到的距离是( )
A.2 B. C. D.
3.如图,四边形ABCD内接于⊙O,若,则∠BCD的度数是( )
A.50° B.80° C.100° D.130°
4.如图,AB为⊙O的直径,半径OA的垂直平分线交⊙O于点C,D,P为优弧ABC上一点,则∠APC=( )
A.20° B.30° C.35° D.40°
5.如图,已知AB为⊙O的直径,点C在⊙O上,∠A=15°,则∠BOC的度数为( )
A.15° B.30° C.45° D.60°
6.如图,内接于,,D是边BC的中点,连接OD并延长,交于点E,则的大小为( )
A. B. C. D.
7.如图,在⊙O中,所对的圆周角∠ACB=70°,若P为一点,∠AOP=75°,则∠POB的度数为( )
A.50° B.65° C.75° D.80°
8.如图,是的直径,是上一点,若,则的度数是( )
A. B. C. D.
9.如图,点A,B,C是⊙O上的三点,若,,则∠AOB的大小为( )
A.25° B.30° C.35° D.40°
10.如图,在RtABC中,∠CAB=36°,斜边AC与量角器的直径重合(A点的刻度为0),将射线BF绕着点B转动,与量角器的外圆弧交于点D,与AC交于点E,若ABE是等腰三角形,则点D在量角器上对应的刻度为( )
A.72° B.144° C.36°或72° D.72°或144°
评卷人得分
二、填空题(每小题5分,共5各小题,共计25分)
11.如图,在中,弦半径,则的度数为____________.
12.如图正方形的边长为1,分别以正方形的两个相对顶点为圆心,以1为半径画弧,则图中阴影部分的面积是______(用含有的式子表示).
13.如图,⊙O的半径为2,弦AB=,点C是弦AB上一动点,OC长为整数,则OC的长为______.
14.把一个球放入长方体纸盒,球的一部分露出盒外,球与纸盒内壁都刚好相切,其截面如图所示,若露出部分的高度为6cm,AF=DE=3cm,则这个球的半径是_____cm.
15.如图,在半径为10cm的⊙O中,弦AB=12cm,OC⊥AB,垂足为C,则OC的长为 _____cm.
评卷人得分
三、解答题(16、17、18题9分,19题8分,共计35分)
16.在⊙O中,弦AB⊥AC,且AB=AC=6.D是⊙O上一点(不在上),连接AD、BD、CD.
(1)如图①,若AD经过圆心O,求BD、CD的长;
(2)如图②,若∠BAD=2∠DAC,连接BC、OD,且BC是直径,求BD、CD的长.
17.定义:如图1,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股点.已知点M、N是线段AB的勾股点.
(1)若AM=1,MN=2,则BN= ;
(2)如图2,DE是△ABC的中位线,M、N是AB边的勾股点(AM<MN<NB),连接CM、CN分别交DE于点G、H.求证:G、H是线段DE的勾股点.
(3)如图3,C,D是线段AB的勾股点(AC
(1)求直径的长;
(2)若,计算图中阴影部分的面积.
19.如图,点A、B、C在⊙O上, AB=CB=9, AD∥BC,CD⊥AD,且AD=2.
(1)求线段CD、AC的长;
(2)求⊙O的半径.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C【分析】根据垂径定理可得:,DE=CE,进而得到∠COE=∠DOE,无法得到OE=BE.
【详解】∵AB是⊙O的直径,CD为弦,CD⊥AB于点E,
∴,DE=CE,,
∴B,D选项正确;
∵,
∴,
∴∠COE=∠DOE,
∴A选项正确;
只有当∠COE=60°时,才有OE=BE.
∴C选项不成立;
故选:C.
【点睛】本题考查了垂径定理和圆心角、弧之间的关系.解题的关键是熟练掌握垂径定理.垂径定理:垂直弦的直径平分弦,并且平分弦所对的弧.
2.A【分析】连接,过点,分别作与,于,则四边形是矩形,证明,可得,根据垂径定理可得,根据即可求解.
【详解】连接,过点,分别作于,于,则四边形是矩形,
,,
,
,
,
(HL),
,
则,
,
,
,
.
故选:A.
【点睛】本题考查了垂径定理,掌握垂径定理是解题的关键.
3.D【分析】根据圆周角定理求出∠A的度数,根据圆内接四边形的性质得出∠A+∠BCD=180°即可解答.
【详解】解:∵弧BCD对的圆周角是∠A,圆心角是∠BOD=100°,
∴∠A=∠BOD=50°,
∵A、B、C、D四点共圆,
∴∠A+∠BCD=180°,
∴∠BCD=130°.
故选:D.
【点睛】本题主要考查了圆周角定理、圆内接四边形的性质等知识点,根据圆周角定理求得∠A的度数和得出∠A+∠BCD=180°是解答本题的关键.
4.B【分析】连接OC,设DC与OA的交点为E,则OE=,求得∠OCE=30°,∠AOC=60°,根据圆周角定理计算即可.
【详解】如图,连接OC,设DC与OA的交点为E,
根据题意,AB为⊙O的直径,半径OA的垂直平分线交⊙O于点C,D,
得OE=,
∴∠OCE=30°,∠AOC=60°,
∴∠APC==30°,
故选B.
【点睛】本题考查了垂径定理,圆周角定理,勾股定理,直角三角形的性质,熟练掌握垂径定理,圆周角定理是解题的关键.
5.B【分析】根据圆周角定理解答.
【详解】解:∠BOC=2∠BAC=2×15°=30°,
故选:B.
【点睛】本题考查了圆周角定理,要知道,同弧所对的圆周角是它所对圆心角的一半.
6.C【分析】连接CE,根据圆内接四边形的性质得到∠BEC=180°﹣∠A=140°,根据垂径定理得到OE⊥BC,求得BD=CD,根据等腰三角形的性质即可得到结论.
【详解】解:如下图,连接CD,
∵∠A=40°,
∴∠BEC=180°﹣∠A=140°,
∵D是边BC的中点,
∴OE⊥BC,BD=CD,
∴BE=CE,
∴.
故选:C.
【点睛】本题考查了圆内接四边形的性质、垂径定理、等腰三角形的性质等知识,正确理解题意是解题的关键.
7.B【分析】先利用圆周角定理得到∠AOB=2∠ACB=140°,然后根据角的和差求解即可.
【详解】解:∵所对的圆周角∠ACB=70°,
∴∠AOB=2∠ACB=2×70°=140°,
∵∠AOP=75°,
∴∠POB=∠AOB-∠AOP=140°-75°=65°.
故选:B.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
8.B【分析】根据直径所对的圆周角是直角,直角三角形的两个锐角互余计算判断即可.
【详解】∵ 是的直径,
∴
∵ ,
∴=58°,
故选B.
【点睛】本题考查了圆周角定理,直角三角形的性质,熟练掌握圆周角定理是解题的关键.
9.A【分析】根据“同弧所对的圆周角是圆心角的一半”可求出,由图可知∠AOB=,即可求解.
【详解】∵,
∴,
∵,
∴∠AOB==85°-60°=25°,
故选:A
【点睛】本题主要考查了圆心角和圆周角,熟练地掌握“同弧所对的圆周角是圆心角的一半”是解题的关键.
10.D【分析】如图,点O是AC中点,连接DO,易知点D在量角器上对应的度数=∠AOD=-∠DOC=2∠DBC,只要求出∠DBC的度数即可解决问题.
【详解】解:如图,点O是AB中点,连接DO,
点D在量角器上对应的度数=∠AOD=-∠DOC=-2∠DBC,
∵ABE是等腰三角形,
当为顶角时,
,
,
∠DOC=2∠DBC=,
∴点D在量角器上对应的度数=;
当为底角时,
,
,
∠DOC=2∠DBC=,
点D在量角器上对应的度数=.
故选:D.
【点睛】本题考查圆心角与圆周角的关系,量角器、等腰三角形的判定和性质等知识,解题的关键是理解∠COD=2∠CBD,学会分类讨论的思想.
11.100°##100度【分析】先根据平行线的性质求出∠OCA的度数,再根据等边对等角求出∠OAC的度数,即可利用三角形内角和定理求出∠AOC的度数.
【详解】解:∵,
∴∠OCA=∠BOC=40°,
∵OA=OC,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°-∠OAC-∠OCA=100°,
故答案为:100°.
【点睛】本题主要考查了平行线的性质,圆的基本性质,三角形内角和定理,等腰三角形的性质,熟知相关知识是解题的关键.
12.【分析】利用两个圆的面积减去一个正方形的面积求解即可.
【详解】解:如图所示
S阴影=-S正方形=-12=.
故答案为:.
【点睛】本题考查阴影面积的求解,利用S阴影=-S正方形进行求解是解决本题的关键.
13.1或2【分析】作OH⊥AB于H,根据垂径定理得AH=BH=AB=,再在Rt△BOH中,根据勾股定理得OH=1,再求出OC的取值范围,最后可得答案.
【详解】解:作OH⊥AB于H,如图,
∵OH⊥AB,
∴AH=BH,
∴AH=BH=AB=×=,
在Rt△BOH中,OB=2,BH=,
∴OH=,
∵点C是弦AB上一动点,
∴
∵OC长为整数,
∴OC=1或2,
故答案为:1或2
【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
14.15【分析】过作于,交于,连接,设半径为,根据勾股定理列方程即可得到结论.
【详解】解:过作于,交于,连接,
,
,
设半径为,则,,,
根据勾股定理得,,
解得:或3(舍,
答:这个球的半径为.
故答案为:15.
【点睛】本题考查了垂径定理及勾股定理的知识,解题的关键是正确的作出辅助线构造直角三角形.
15.8【分析】根据“垂径定理”即可得出AC的长度,连接AO,构建直角三角形,用勾股定理即可求出OC.
【详解】连接AO,
∵OC⊥AB,且AB=12cm,
∴AC=6cm
∵半径为10cm
∴AO=10cm
在Rt△AOC中,由勾股定理可得:OC=cm
故答案为:8
【点睛】本题主要考查了“垂径定理”的运用,垂直于直径的弦被直径平分.熟练地掌握垂径定理并能够根据题意构建直角三角形是解题的关键.
16.(1)BD=6,CD=6
(2),BD=
【分析】(1)由AD经过圆心O,利用圆周角定理得∠ACD=∠ABD=90°,又因为AB⊥AC,得到四边形ABCD为矩形,易得结果;
(2)由∠BAD=2∠DAC,AB⊥AC,由圆周角定理得BC为直径,易得∠CAD=30°,∠BAD=60°,证明△COD为等边三角形,求得CD,BD.
(1)
解:AD是⊙O的直径,
∴∠C=∠B=90°,
∵AB⊥AC,
∴∠BAC=90°,
∴四边形ABDC是矩形,
∵AB=AC=6,
∴BD=AC=6,CD=AB=6;
(2)
∵∠BAC=90°,∠BAD=2∠DAC,
∴∠BAD=60°,∠DAC=30°,
∴∠COD=2∠CAD=60°,
∵OC=OD,
∴△COD是等边三角形,
∴CD=OC,
在Rt△ABC中,,
∴,
在Rt△BCD中,.
【点睛】本题主要考查了圆周角定理、勾股定理、等边三角形的判定和性质、矩形的判定和性质等知识,熟练掌握相关定理是解答此题的关键.
17.(1)或
(2)见解析
(3)
【分析】(1)根据题意分两类进行讨论,并由勾股定理求解即可.
(2)根据DE是△ABC的中位线,可得,并且分别为各边的中点,然后得到分别为中位线,最后根据题意列出关系式,即可得证.
(3)连接PD,由题意可得,根据圆周角定理可知∠CPD=90°,再由勾股定理,得到以及各角间的关系,从而求出的度数,进而得到结论.
(1)
解:∵点M、N是线段AB的勾股点,
∴或
∴BN的长为;
故答案为:;
(2)
证明:如图2,
∵DE是△ABC的中位线,
∴DE∥AB,CD=AD,CE=BE,
∴CG=GM,CH=HN,
∴DG=AM,GH=MN,EH=BN,
∵M、N是AB边的勾股点(AM<MN<NB),
∴BN2=MN2+AM2,
∴BN2=MN2+AM2,
∴(BN)2=(MN)2+(AM)2,
∴EH2=GH2+DG2,
∴G、H是线段DE的勾股点;
(3)
解:如图3,连接PD,
∵AC=PC,
∴∠A=∠APC,
∴∠PCD=2∠A,
∵C,D是线段AB的勾股点,
∴AC2+BD2=CD2,
∴PC2+BD2=CD2,
∵CD是⊙O的直径,
∴∠CPD=90°,
∴PC2+PD2=CD2,
∴PD=BD,
∴∠PDC=2∠B,
∵∠A=2∠B,
∴∠PDC=∠A,
在Rt△PCD中,∵∠PCD+∠PDC=90°,
∴2∠A+∠A=90°,
∴∠A=30°,
∴∠B=∠A=15°.
【点睛】此题主要考查了圆的有关知识、勾股定理以及新定义勾股点的理解和运用,解题关键是对新定义的理解与运用.
18.(1)4
(2)6
【分析】(1)设辅助线,利用直径、角平分线的性质得出的度数,利用圆周角与圆心角的关系得出的度数,根据半径与直径的关系,结合勾股定理即可得出结论.
(2)由(1)已知,得出的度数,根据圆周角的性质结合得出,再根据直径、等腰直角三角形的性质得出的值,进而利用直角三角形面积公式求出,由阴影部分面积可知即为所求.
(1)解:如图所示,连接,为的直径,平分,,,..,,,即...
(2)解:如图所示,设其中小阴影面积为,大阴影面积为,弦与劣弧所形成的面积为,由(1)已知,,,,.,弦弦,劣弧劣弧..为的直径,,,.,...
【点睛】本题考查圆的性质的理解与综合应用能力.涉及对半径与直径的关系,直径的性质,圆周角与圆心角的关系,圆周角的性质,勾股定理,直角三角形,角平分线等知识点.半径等于直径的一半;直径所对的圆周角是直角;在同圆或等圆中,相等的弦所对的圆周角等于圆心角的一半;在同圆或等圆中,圆周角相等弧相等弦相等.一个直角三角中,两个直角边边长的平方加起来等于斜边长的平方.恰当借助辅助线,灵活运用圆周角的性质建立等式关系是解本题的关键.
19.(1)CD=;AC=6
(2)
【分析】(1)作AE⊥BC于E,易证四边形AECD为矩形,可得EC=AD=2,BE=BC EC=7,再利用勾股定理求解即可;
(2)连接AO并延长交⊙O于点F,连接BF,证明△ABF∽△CDA,利用相似三角形的性质求出AF即可.
(1)解:作AE⊥BC,垂足为E,∵AD∥BC,∴AE⊥AD,∵CD⊥AD,∴四边形AECD为矩形,∴EC=AD=2,∴BE=9-2=7,∴在Rt△AEB中,AE2=AB2-BE2=32,在Rt△AEC中,AC2=AE2+CE2=36,∴AC=6,在Rt△ACD中,CD=;
(2)连接AO并延长交⊙O于点F,连接BF,∴∠F=∠ACB,∵AD∥BC,∴∠DAC=∠ACB,∴∠F=∠DAC,∵AF为⊙O的直径,∴∠ABF=90°,∴∠ADC=∠ABF=90°, ∴△ABF∽△CDA,∴,∵四边形AECD为矩形,∴CD=AE=,∴,∴AF=,∴⊙O的半径r=.
【点睛】本题考查了矩形的判定和性质,勾股定理,平行线的性质,圆周角定理,相似三角形的判定和性质等知识,作出合适的辅助线构造出直角三角形和相似三角形是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
