2021-2022学年江西省各地人教版七年级数学上册2.1整式期末试题分类选编(word、含解析)
文档属性
| 名称 | 2021-2022学年江西省各地人教版七年级数学上册2.1整式期末试题分类选编(word、含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 370.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 00:00:00 | ||
图片预览




文档简介
2.1 整式
1.(2022·江西上饶·七年级期末)对于单项式,下列说法中正确的是( )
A.系数是,次数是 B.系数是,次数是
C.系数是,次数是 D.系数是,次数是
2.(2022·江西上饶·七年级期末)下列结论正确的是( )
A.的系数是0 B.中二次项的系数是1
C.的次数是5 D.的次数是2
3.(2022·江西赣州·七年级期末)下列说法正确的是( )
A.的系数是 B.是三次三项式
C.的常数项是1 D.是多项式
4.(2022·江西赣州·七年级期末)根据下表中提供的四个数的变化规律,则的值为( )
1 4 2 6 3 8 4 10 20
2 9 3 20 4 35 5 54 … m x
第1个 第2个 第3个 第4个 第个
A.252 B.209 C.170 D.135
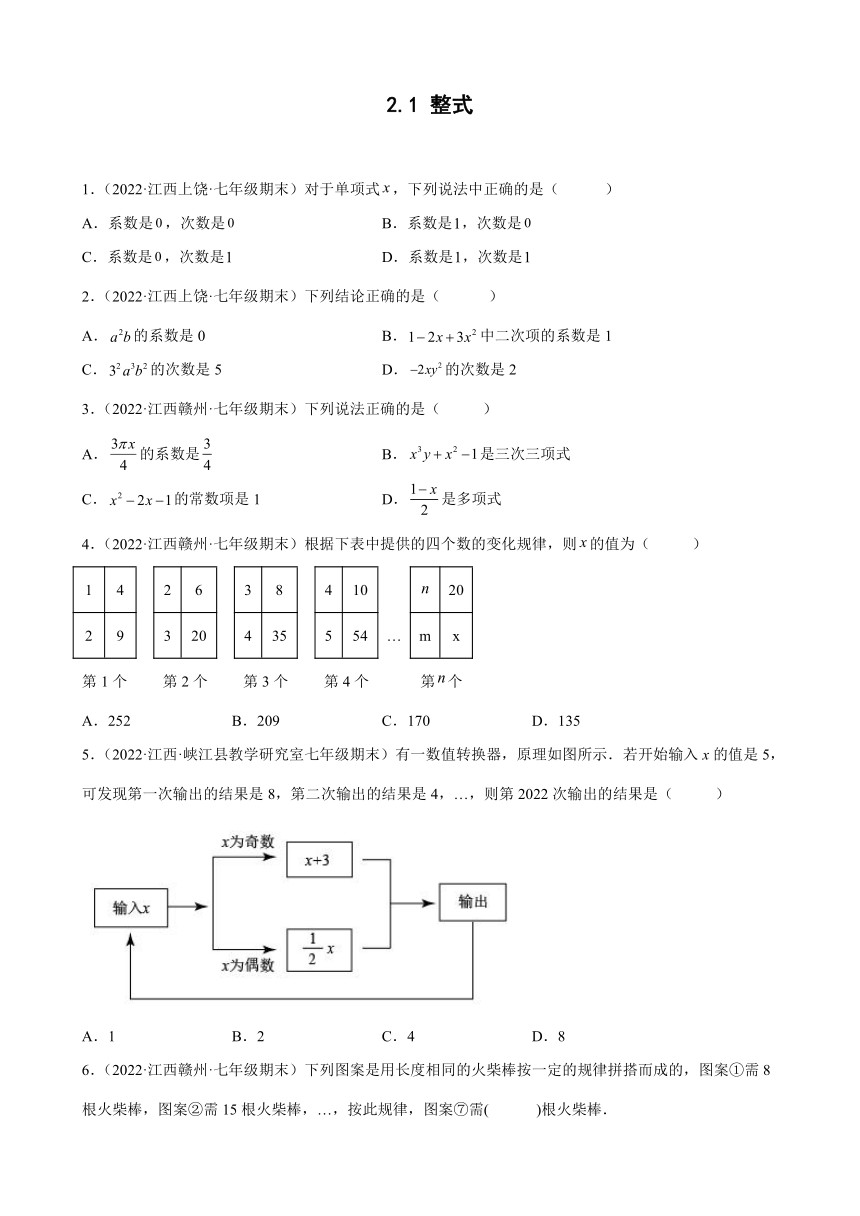
5.(2022·江西·峡江县教学研究室七年级期末)有一数值转换器,原理如图所示.若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,则第2022次输出的结果是( )
A.1 B.2 C.4 D.8
6.(2022·江西赣州·七年级期末)下列图案是用长度相同的火柴棒按一定的规律拼搭而成的,图案①需8根火柴棒,图案②需15根火柴棒,…,按此规律,图案⑦需( )根火柴棒.
A.48 B.49 C.50 D.51
7.(2022·江西赣州·七年级期末)观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球个数( )
A.600 B.601 C.602 D.1002
8.(2022·江西吉安·七年级期末)我县某公园内有一段直线步道,其地面使用相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成.如图表示此步道的地砖排列方式,其中连续排列的完整正方形地砖共有n个,则该步道上使用的三角形地砖数可表示为( )
A.2n+2 B.2n+4 C.3n+3 D.4n+2
9.(2022·江西景德镇·七年级期末)用长的铝合金做成一个长方形的窗框(如图,单位:),设长方形窗框的横条长度为,则长方形窗框的面积为( )
A. B. C. D.
10.(2022·江西吉安·七年级期末)长度相同的木棒按一定规律拼搭图案,第1个需7根木棒,第2个需13根木棒,…,第11个需要木棒的个数为( )
A.156 B.157 C.158 D.159
11.(2022·江西·南昌市第二十八中学七年级期末)观察等式:;;已知按一定规律排列的一组数:、、、、、.若,用含的式子表示这组数的和是( )
A. B. C. D.
12.(2022·江西赣州·七年级期末)杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”.它是古代重要的数学成就,比西方的“帕斯卡三角形”早了300多年.请仔细观察计算该图中第n行中所有数字之和为( )
A.2n﹣2 B.2n﹣1 C.2n D.2n+1
13.(2022·江西吉安·七年级期末)一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( )
A.2010 B.2011
C.2012 D.2013
14.(2022·江西吉安·七年级期末)单项式的系数是______.
15.(2022·江西吉安·七年级期末)单项式的系数是_______,次数是________.
16.(2022·江西·峡江县教学研究室七年级期末)温度由t°C下降5°C后是___________°C.
17.(2022·江西赣州·七年级期末)一个单项式中只含字母a、b且单项式次数为4,请你写出三个符合条件的不同类型的单项式:____________、____________、____________.(说明:xy与-2xy可看成同一类型)
18.(2022·江西宜春·七年级期末)按一般规律排列的一列数依次为:,,,,,……,按此规律排列下去,这列数中的第2021个数是______.
19.(2022·江西抚州·七年级期末)如图所示,是一个运算程序示意图.若第一次输入k的值为125,则第2022次输出的结果是______.
20.(2022·江西吉安·七年级期末)某玩具店将进货价为元的玩具以元的销售价售出,平均每月能售出个市场调研表明:当销售价每涨价元时,其销售量将减少2个.
(1)设每个玩具的销售价上涨元,试用含的式子填空:
①涨价后,每个玩具的销售价为 元;
②涨价后,每个玩具的利润为 元;
③涨价后,玩具的月销售量为 个.
(2)玩具店老板要想让该玩具的销售利润平均每月达到1600元,销售员甲说:“在原售价每个90元的基础上再上涨30元,可以完成任务”销售员乙说:“不用涨那么多,在原售价每个90元的基础上再上涨10元就可以了”判断销售员甲与销售员乙的说法是否正确,并说明理由.
21.(2022·江西吉安·七年级期末)如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.6厘米,每个铁环长4厘米,设铁环间处于最大限度的拉伸状态.
(1)2个、3个、4个铁环组成的链条长分别有多少
(2)设n个铁环长为y厘米,请用含n的式子表示y;
(3)若要组成1.44米长的链条,需要多少个铁环
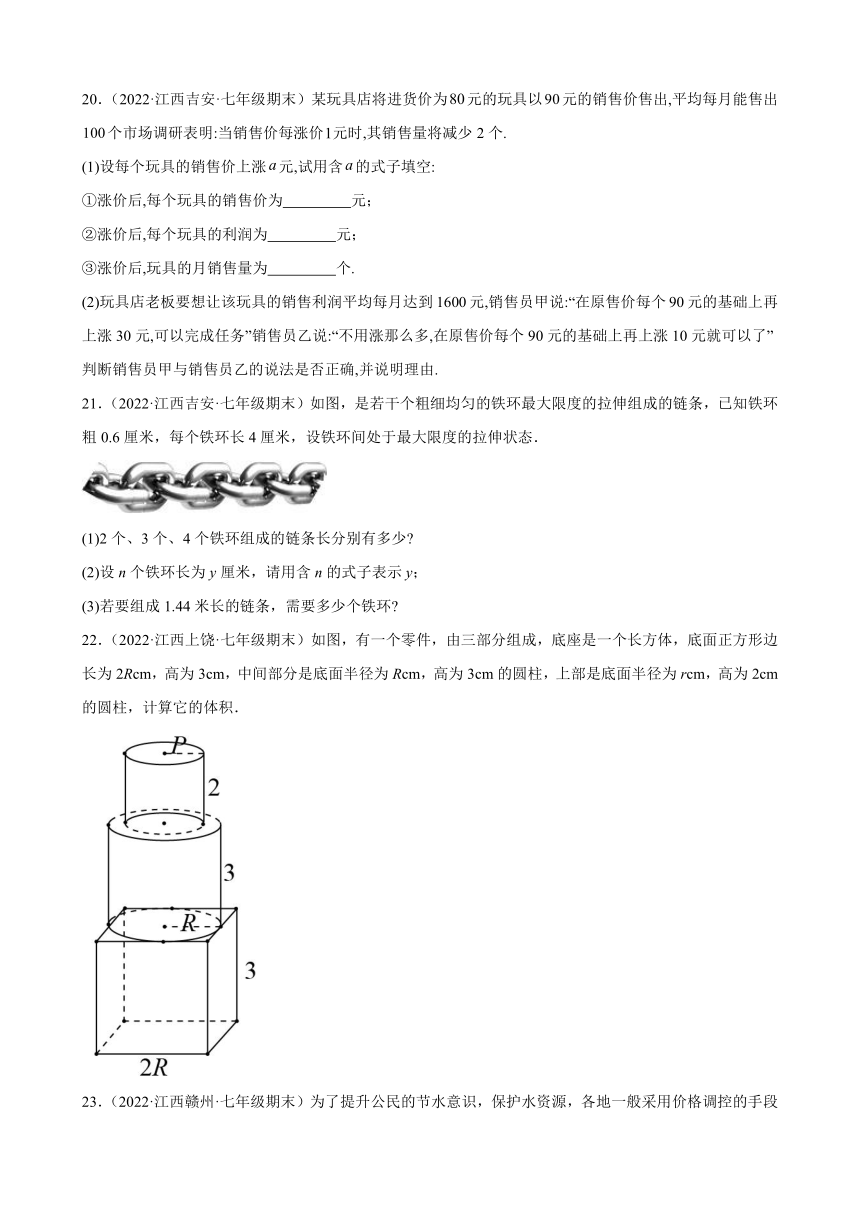
22.(2022·江西上饶·七年级期末)如图,有一个零件,由三部分组成,底座是一个长方体,底面正方形边长为2Rcm,高为3cm,中间部分是底面半径为Rcm,高为3cm的圆柱,上部是底面半径为rcm,高为2cm的圆柱,计算它的体积.
23.(2022·江西赣州·七年级期末)为了提升公民的节水意识,保护水资源,各地一般采用价格调控的手段达到节水的目的.某市自来水收费的收费标准如下表:
每月用水量 单价(元/立方米)
不超过16立方米的部分 3
超过16立方米不超过24立方米的部分 4
超过24立方米的部分 6.5
(1)在某户居民2月份用水12立方米,则应收水费多少元?
(2)若某户居民4月份用水m立方米(其中16<m≤24),请用含有m的代数式表示应收水费.
(3)某户居民5、6月份共用水40立方米(5月份用水量超过了16立方米),设6月份用水n立方米,请用含有n的代数式表示该居民5、6两个月共交水费多少元?
24.(2022·江西上饶·七年级期末)(1)有一列数1、3、5、7……有无数项(无数个数),请观察其规律后写出其中第20项(从左往右数第20个数)是 ,第n项是 ;
(2)二算法是数学的一种很重要的方法,用二算法可以得到许多很重要的数学公式.请观察下图,用二算法推导出1+3、1+3+5、1+3+5+7的计算结果,猜测1+3+5+7+……+(2n-1)的计算结果;
(3)由(2)推导出2+4+6+……+2n的结果.
参考答案:
1.D【解析】根据单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
解:单项式的系数是1,次数是1,
故选:D.
本题考查了单项式,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.
2.C【解析】根据单项式的系数判断A选项;根据多项式的项判断B选项;根据单项式的次数判断C,D选项.
解:A选项,a2b的系数为1,故该选项不符合题意;
B选项,1-2x+3x2中二次项的系数是3,故该选项不符合题意;
C选项,32a3b2的次数是3+2=5,故该选项符合题意;
D选项,-2xy2的次数是1+2=3,故该选项不符合题意;
故选:C.
本题考查了单项式,多项式,掌握单项式中所有字母的指数和是单项式的次数是解题的关键.
3.D【解析】根据单项式与多项式的定义、系数、次数逐项分析判断即可.
A.的系数是 故A选项错误,不符合题意.
B. 是四次三项式,故B选项错误,不符合题意.
C. 的常数项是-1,故C选项错误,不符合题意.
D.是二项式,是多项式,故D选项正确,符合题意.
故选D
本题主要考查了单项式与多项式的定义、系数、次数.单项式中的数字因数叫做单项式的系数,注意是一个常数.几个单项式的和叫做多项式,一个多项式中次数最高的项的次数叫做这个多项式的次数,其中不含字母的项叫做常数项,注意每一项都要包含前面的符号.掌握这些基本概念是解题的关键.
4.B【解析】观察表格,分别得出四个数字之间的关系,依照规律解答.
解:观察可知:
表格中左上的数为从1开始的连续自然数,
左下的数为从2开始的连续自然数,
右上的数为左下的数的2倍,
右下角的数等于右上角与左下角的两个数的积与左上角数的和,
∴n=20÷2-1=9,m=20÷2=10,
∴x=20m+n=209,
故选B.
此题考查的是数字的变化规律,猜想各个数之间的联系是解题的关键.
5.B【解析】输入为奇数代入中第1次输出为8;输入为偶数代入中第2次输出为4;输入为偶数代入中第3次输出为2;输入为偶数代入中第4次输出为1;输入为奇数代入中第5次输出为4;输入为偶数代入中第6次输出为2;输入为偶数代入中第7次输出为1;推导一般规律,然后进行求解即可.
解:输入为奇数代入中第1次输出为8;
输入为偶数代入中第2次输出为4;
输入为偶数代入中第3次输出为2;
输入为偶数代入中第4次输出为1;
输入为奇数代入中第5次输出为4;
输入为偶数代入中第6次输出为2;
输入为偶数代入中第7次输出为1;
故可得出之后每次的输出数值均为的循环
∵
∴第2022次输出结果为2
故选B.
本题考查了程序流程图与代数式求值.解题的关键是通过求解代数式的值推导出一般规律.
6.C【解析】根据图案①、②、③中火柴棒的数量可知,第1个图形中火柴棒有8根,然后每多一个多边形就多7根火柴棒,由此可知第n个图案需火柴棒8+7(n 1)=7n+1根,令n=7可得答案.
解:∵图案①需火柴棒:8根;
图案②需火柴棒:8+7=15根;
图案③需火柴棒:8+7+7=22根;
…
∴图案n需火柴棒:8+7(n 1)=7n+1根;
当n=7时,7n+1=7×7+1=50,
∴图案⑦需50根火柴棒,
故选C.
此题主要考查了图形的变化类,解决此类题目的关键在于准确的找出图形在变化过程中不变的部分和变化的部分,变化部分是以何种规律变化.
7.B【解析】由图可知:●○○●●○○○○○每10个图形一循环,然后每组循环组里面有3个实心球,从而确定在2004个球中一共有多少个循环组,进一步得出答案即可.
解:∵●○○●●○○○○○每10个球一循环且每组循环组里面有3个实心球
∴2004÷10=200…4,第2004个是实心球,
则共有实现球200×3+1=601个.
故选:B.
此题考查图形的变化规律,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,找出循环的规律解决问题.
8.B【解析】由图可知,每个灰色正方形地砖右侧都有两个与之相邻的三角形地砖,而在整个步道的两侧尽头一共有4个三角形地砖,据此求解即可.
解:由图可知,每个灰色正方形地砖右侧都有两个与之相邻的三角形地砖,而在整个步道的两侧尽头一共有4个三角形地砖,
∴该步道上使用的三角形地砖数可表示为,
故选B.
本题主要考查了图形类的规律,正确理解题意找到规律是解题的关键.
9.C【解析】根据长方形窗框的横条长度求出长方形窗框的竖条长度,再根据长方形的面积公式计算即可求解.
解:∵长方形窗框的横条长度为m
∴长方形窗框的竖条长度为m
∴长方形窗框的面积为:m2
故选C.
本题考查了列代数式,要注意长方形窗框的横条有3条,观察图形求出长方形窗框的竖条长度是解答本题的关键.
10.B【解析】分别求出每一个图形的木棒数,然后再找出一般规律求解即可.
解:第1个图形共有7=1×(1+3)+3根木棒,
第2个图形共有13=2×(2+3)+3根木棒,
第3个图形共有21=3×(3+3)+3根木棒,
第4个图形共有31=4×(4+3)+3根木棒,
…
第n个图形共有n×(n+3)+3根木棒,
第11个图形共有11×(11+3)+3=157根木棒,
故选:B
此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.
11.C【解析】根据题意,一组数:、、、、、的和为250+251+252+…+299+2100==a+(2+22+…+250)a,进而根据所给等式的规律,可以发现2+22+…+250=251-2,由此即可求得答案.
250+251+252+…+299+2100
=a+2a+22a+…+250a
=a+(2+22+…+250)a,
∵,
,
,
…,
∴2+22+…+250=251-2,
∴250+251+252+…+299+2100
=a+(2+22+…+250)a
=a+(251-2)a
=a+(2 a-2)a
=2a2-a ,
故选C.
本题考查了规律题——数字的变化类,仔细观察,发现其中哪些发生了变化,哪些没有发生变化,是按什么规律变化的是解题的关键.
12.B【解析】由题意得出每行的数字之和等于2的序数减一次幂,据此解答即可.
∵第1行数字之和1=20,
第2行数字之和2=21,
第3行数字之和4=22,
第4行数字之和8=23,
…
∴第n行中所有数字之和为2n﹣1.
故选:B.
本题主要考查数字的变化类,解题的关键是每行的数相加,分析总结得出规律,根据规律求出第n行的数据之和.
13.D由题意设被截去部分为5n+2+1=5n+3
从其选项中看,故选D.
14.【解析】根据二次根式的定义,即可求解.
解:单项式的系数是.
故答案为:
本题主要考查了单项式的系数和次数的定义,熟练掌握单项式中的数字因式是单项式的系数,所有字母的和是单项式的次数是解题的关键.
15. 2【解析】根据单项式的系数定义“是指单项式中的数字因数”、次数的定义“是指所有字母的指数的和”即可得.
由单项式的系数与次数定义得:单项式的系数是,次数是
故答案为:,2.
本题考查了单项式的相关概念,熟记概念是解题关键.
16.(t-5)【解析】根据题意列出运算式子即可得.
由题意得:.
故答案为:.
本题考查了有理数减法的实际应用,依据题意,正确列出运算式子是解题关键.
17. 【解析】根据题意可知,只含字母a、b且单项式次数为4,可分三种情况:字母a的为3次,b为1次;字母a的为2次,b为2次;字母a的为1次,b为3次;由此即可作答.
单项式的次数是指单项式中所有字母因数的指数和,此题符合条件的不同类型的单项式可以是,,.
故答案为:,,.
本题主要考查了单项式次数的概念,解题的关键是掌握单项式的次数.
18.##【解析】观察发现,分子的规律:分子是常数1;分母的规律:第奇数项的分母为:,第偶数项的分母为:,据此写出第2021个数
分子的规律:分子是常数1;
分母的规律:第1个数的分母为:,
第2个数的分母为:,
第3个数的分母为:,
第4个数的分母为:,
第5个数的分母为:,
第6个数的分母为:,
…第奇数项的分母为:,第偶数项的分母为:,
所以第2021个数是
故答案为:
本题考查了数字类规律题,找到规律是解题的关键.
19.5【解析】根据程序计算多次,寻找出其中的规律,从第三次开始,出现1,5循环,计算(2022-2)÷2,确定余数,判断即可.
当k=125时,
第1次输出结果为,
第2次输出结果为,
第3次输出结果为,
第4次输出结果为,
第5次输出结果为,
第6次输出结果为,
从第三次开始,出现1,5循环,且奇数次为1,偶数次为为5,
∴第2022次输出的结果是5,
故答案为:5.
本题考查了有理数的混合运算,有理数中的规律,熟练计算,规范寻找循环节,确定变化规律是解题的关键.
20.(1)①(90+a);②(10+a);③(100-2a);(2)销售员甲与销售员乙的说法都正确,理由见解析【解析】(1)①根据题意,即可求出涨价后,每个玩具的销售价;
②根据题意,即可求出涨价后,每个玩具的利润;
③根据“销售价每涨价元时,其销售量将减少2个”,即可求出涨价后,玩具的月销售量;
(2)根据题意,分别求出上涨30元和上涨10元后每月的销售利润,即可判断.
解:(1)①根据题意,涨价后,每个玩具的销售价为(90+a)元
故答案为:(90+a);
②根据题意,涨价后,每个玩具的利润为90+a-80=(10+a)元
故答案为:(10+a);
③根据题意,涨价后,玩具的月销售量为(100-2a)元
故答案为:(100-2a);
(2)销售员甲与销售员乙的说法都正确,理由如下
若上涨30元,每月的销售利润为(90+30-80)×(100-30×2)=1600元
故甲正确;
若上涨10元,每月的销售利润为(90+10-80)×(100-10×2)=1600元
故乙正确.
故销售员甲与销售员乙的说法都正确.
此题考查的是列代数式表示实际意义,掌握实际问题中的各个量之间的关系是解决此题的关键.
21.(1)2个铁环组成的链条长6.8cm,3个铁环组成的链条长为9.6cm,4个铁环组成的链条长12.4cm
(2)y=2.8n+1.2
(3)需要51个铁环
【解析】根据观察,i链条每一个连处重合的部分是两个铁环的直径,根据题意列出算式求解即可.
(1)
由题意可得:4×2-0.6×2=6.8cm,4×3-0.6×4=9.6cm,4×4-0.6×6=12.4cm.
故2个铁环组成的链条长6.8cm,3个铁环组成的链条长为9.6cm,4个铁环组成的链条长12.4cm;
(2)
y=4n-2(n-1)×0.6,即y=2.8n+1.2;
(3)
1.44米=144cm据题意有2.8n+1.2=144,解得:n=51,
答:需要51个铁环.
本题主要考查了有理数的计算和用字母表示数,准确得根据题目和图形找出等量关系列出代数式是解题的关键.
22.(12R2+3πR2+2πr2)cm3【解析】先分别计算每个几何体体积,再相加.
解:由题意得:体积V=(2R)2×3+πR2×3+πr2×2
=(12R2+3πR2+2πr2)cm3.
答:该几何体的体积是(12R2+3πR2+2πr2)cm3.
本题考查几何体体积的计算,掌握各个几何体体积计算公式是求解本题的关键.
23.(1)应收水费36元
(2)应收水费为(4m-16)元
(3)一共要交128元或(184-3.5n)元
【解析】(1)利用用水量的范围计算结果即可;
(2)根据m的取值范围,先计算超过16立方米的费用,超过16立方米的用水量为(m﹣16)立方米,根据费用可计算结果;
(3)根据题意可列出5月份用水量的代数式,分情况讨论,若5月份用水(40﹣n)立方米不超过24立方米,根据题意列代数式计算5、6月份水费即可,若5月份用水(40﹣n)立方米超过24立方米,根据题意列代数式计算5、6月份水费即可,注意计算6月份用水量的范围.
(1)解:12×3=36(元);答:某居民2月份用水12立方米,应收水费36元;
(2)解:应收水费,16×3+(m-16)×4=4m-16(元).答:某户居民4月份应收水费为(4m-16)元
(3)解:6月份用水n立方米,则5月份用水(40-n)立方米,①若5月份用水(40-n)立方米不超过24立方米,则5月份水费为16×3+(40-n-16)×4=(144-4n)(元),因为16<40-n≤24,所以16≤n<24,则6月份水费为16×3+(n-16)×4=(4n-16)(元),所以5、6月份水费合计:(144-4n)+(4n-16)=128(元);②若5月份用水(40-n)立方米超过24立方米,则5月份水费为16×3+8×4+(40-n-24)×6.5=(184-6.5n)(元),因为40-n>24,所以n<16,则6月份水费为n×3=3n(元)所以5、6月份水费合计:(184-6.5n)+3n=(184-3.5n)(元);答:5、6月份水费一共要交128元或 (184-3.5n)元.
本题主要考查列代数式,找出题目蕴含的数量关系是解决问题的关键.
24.(1)39; 2n-1;(2) n2;(3)n2+n【解析】(1)由所给的数字可得第n个数为2n﹣1,据此解答即可;
(2)对所给的图形进行分析,总结出规律即可;
(3)利用(2)的方式进行求解即可.
解:(1)∵一列数1、3、5、7…,
∴第n个数为:2n﹣1,
∴第20个数为:2×20﹣1=39,
故答案为:39,2n﹣1;
(2)第(2)图中,分层小正方形的个数是(1+3)个,而整体计算小正方形的个数是22,所以,1+3=22;
第(3)图中,分层小正方形的个数是(1+3+5)个,而整体计算小正方形的个数是32,所以,1+3+5=32;
第(4)图中,分层小正方形的个数是(1+3+5+7)个,而整体计算小正方形的个数是42,所以,1+3+5+7=42;
猜测1+3+5+7+…+(2n﹣1)=n2;
(3)2+4+6+8+…+2n
=1+1+3+1+5+1+7+1+…+(2n﹣1)+1
=1+3+5+7+…+(2n﹣1)+n
=n2+n.
本题主要考查数字的变化规律,解答的关键是由所给的数字分析清楚存在的规律.
1.(2022·江西上饶·七年级期末)对于单项式,下列说法中正确的是( )
A.系数是,次数是 B.系数是,次数是
C.系数是,次数是 D.系数是,次数是
2.(2022·江西上饶·七年级期末)下列结论正确的是( )
A.的系数是0 B.中二次项的系数是1
C.的次数是5 D.的次数是2
3.(2022·江西赣州·七年级期末)下列说法正确的是( )
A.的系数是 B.是三次三项式
C.的常数项是1 D.是多项式
4.(2022·江西赣州·七年级期末)根据下表中提供的四个数的变化规律,则的值为( )
1 4 2 6 3 8 4 10 20
2 9 3 20 4 35 5 54 … m x
第1个 第2个 第3个 第4个 第个
A.252 B.209 C.170 D.135
5.(2022·江西·峡江县教学研究室七年级期末)有一数值转换器,原理如图所示.若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,则第2022次输出的结果是( )
A.1 B.2 C.4 D.8
6.(2022·江西赣州·七年级期末)下列图案是用长度相同的火柴棒按一定的规律拼搭而成的,图案①需8根火柴棒,图案②需15根火柴棒,…,按此规律,图案⑦需( )根火柴棒.
A.48 B.49 C.50 D.51
7.(2022·江西赣州·七年级期末)观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球个数( )
A.600 B.601 C.602 D.1002
8.(2022·江西吉安·七年级期末)我县某公园内有一段直线步道,其地面使用相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成.如图表示此步道的地砖排列方式,其中连续排列的完整正方形地砖共有n个,则该步道上使用的三角形地砖数可表示为( )
A.2n+2 B.2n+4 C.3n+3 D.4n+2
9.(2022·江西景德镇·七年级期末)用长的铝合金做成一个长方形的窗框(如图,单位:),设长方形窗框的横条长度为,则长方形窗框的面积为( )
A. B. C. D.
10.(2022·江西吉安·七年级期末)长度相同的木棒按一定规律拼搭图案,第1个需7根木棒,第2个需13根木棒,…,第11个需要木棒的个数为( )
A.156 B.157 C.158 D.159
11.(2022·江西·南昌市第二十八中学七年级期末)观察等式:;;已知按一定规律排列的一组数:、、、、、.若,用含的式子表示这组数的和是( )
A. B. C. D.
12.(2022·江西赣州·七年级期末)杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”.它是古代重要的数学成就,比西方的“帕斯卡三角形”早了300多年.请仔细观察计算该图中第n行中所有数字之和为( )
A.2n﹣2 B.2n﹣1 C.2n D.2n+1
13.(2022·江西吉安·七年级期末)一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( )
A.2010 B.2011
C.2012 D.2013
14.(2022·江西吉安·七年级期末)单项式的系数是______.
15.(2022·江西吉安·七年级期末)单项式的系数是_______,次数是________.
16.(2022·江西·峡江县教学研究室七年级期末)温度由t°C下降5°C后是___________°C.
17.(2022·江西赣州·七年级期末)一个单项式中只含字母a、b且单项式次数为4,请你写出三个符合条件的不同类型的单项式:____________、____________、____________.(说明:xy与-2xy可看成同一类型)
18.(2022·江西宜春·七年级期末)按一般规律排列的一列数依次为:,,,,,……,按此规律排列下去,这列数中的第2021个数是______.
19.(2022·江西抚州·七年级期末)如图所示,是一个运算程序示意图.若第一次输入k的值为125,则第2022次输出的结果是______.
20.(2022·江西吉安·七年级期末)某玩具店将进货价为元的玩具以元的销售价售出,平均每月能售出个市场调研表明:当销售价每涨价元时,其销售量将减少2个.
(1)设每个玩具的销售价上涨元,试用含的式子填空:
①涨价后,每个玩具的销售价为 元;
②涨价后,每个玩具的利润为 元;
③涨价后,玩具的月销售量为 个.
(2)玩具店老板要想让该玩具的销售利润平均每月达到1600元,销售员甲说:“在原售价每个90元的基础上再上涨30元,可以完成任务”销售员乙说:“不用涨那么多,在原售价每个90元的基础上再上涨10元就可以了”判断销售员甲与销售员乙的说法是否正确,并说明理由.
21.(2022·江西吉安·七年级期末)如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.6厘米,每个铁环长4厘米,设铁环间处于最大限度的拉伸状态.
(1)2个、3个、4个铁环组成的链条长分别有多少
(2)设n个铁环长为y厘米,请用含n的式子表示y;
(3)若要组成1.44米长的链条,需要多少个铁环
22.(2022·江西上饶·七年级期末)如图,有一个零件,由三部分组成,底座是一个长方体,底面正方形边长为2Rcm,高为3cm,中间部分是底面半径为Rcm,高为3cm的圆柱,上部是底面半径为rcm,高为2cm的圆柱,计算它的体积.
23.(2022·江西赣州·七年级期末)为了提升公民的节水意识,保护水资源,各地一般采用价格调控的手段达到节水的目的.某市自来水收费的收费标准如下表:
每月用水量 单价(元/立方米)
不超过16立方米的部分 3
超过16立方米不超过24立方米的部分 4
超过24立方米的部分 6.5
(1)在某户居民2月份用水12立方米,则应收水费多少元?
(2)若某户居民4月份用水m立方米(其中16<m≤24),请用含有m的代数式表示应收水费.
(3)某户居民5、6月份共用水40立方米(5月份用水量超过了16立方米),设6月份用水n立方米,请用含有n的代数式表示该居民5、6两个月共交水费多少元?
24.(2022·江西上饶·七年级期末)(1)有一列数1、3、5、7……有无数项(无数个数),请观察其规律后写出其中第20项(从左往右数第20个数)是 ,第n项是 ;
(2)二算法是数学的一种很重要的方法,用二算法可以得到许多很重要的数学公式.请观察下图,用二算法推导出1+3、1+3+5、1+3+5+7的计算结果,猜测1+3+5+7+……+(2n-1)的计算结果;
(3)由(2)推导出2+4+6+……+2n的结果.
参考答案:
1.D【解析】根据单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
解:单项式的系数是1,次数是1,
故选:D.
本题考查了单项式,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.
2.C【解析】根据单项式的系数判断A选项;根据多项式的项判断B选项;根据单项式的次数判断C,D选项.
解:A选项,a2b的系数为1,故该选项不符合题意;
B选项,1-2x+3x2中二次项的系数是3,故该选项不符合题意;
C选项,32a3b2的次数是3+2=5,故该选项符合题意;
D选项,-2xy2的次数是1+2=3,故该选项不符合题意;
故选:C.
本题考查了单项式,多项式,掌握单项式中所有字母的指数和是单项式的次数是解题的关键.
3.D【解析】根据单项式与多项式的定义、系数、次数逐项分析判断即可.
A.的系数是 故A选项错误,不符合题意.
B. 是四次三项式,故B选项错误,不符合题意.
C. 的常数项是-1,故C选项错误,不符合题意.
D.是二项式,是多项式,故D选项正确,符合题意.
故选D
本题主要考查了单项式与多项式的定义、系数、次数.单项式中的数字因数叫做单项式的系数,注意是一个常数.几个单项式的和叫做多项式,一个多项式中次数最高的项的次数叫做这个多项式的次数,其中不含字母的项叫做常数项,注意每一项都要包含前面的符号.掌握这些基本概念是解题的关键.
4.B【解析】观察表格,分别得出四个数字之间的关系,依照规律解答.
解:观察可知:
表格中左上的数为从1开始的连续自然数,
左下的数为从2开始的连续自然数,
右上的数为左下的数的2倍,
右下角的数等于右上角与左下角的两个数的积与左上角数的和,
∴n=20÷2-1=9,m=20÷2=10,
∴x=20m+n=209,
故选B.
此题考查的是数字的变化规律,猜想各个数之间的联系是解题的关键.
5.B【解析】输入为奇数代入中第1次输出为8;输入为偶数代入中第2次输出为4;输入为偶数代入中第3次输出为2;输入为偶数代入中第4次输出为1;输入为奇数代入中第5次输出为4;输入为偶数代入中第6次输出为2;输入为偶数代入中第7次输出为1;推导一般规律,然后进行求解即可.
解:输入为奇数代入中第1次输出为8;
输入为偶数代入中第2次输出为4;
输入为偶数代入中第3次输出为2;
输入为偶数代入中第4次输出为1;
输入为奇数代入中第5次输出为4;
输入为偶数代入中第6次输出为2;
输入为偶数代入中第7次输出为1;
故可得出之后每次的输出数值均为的循环
∵
∴第2022次输出结果为2
故选B.
本题考查了程序流程图与代数式求值.解题的关键是通过求解代数式的值推导出一般规律.
6.C【解析】根据图案①、②、③中火柴棒的数量可知,第1个图形中火柴棒有8根,然后每多一个多边形就多7根火柴棒,由此可知第n个图案需火柴棒8+7(n 1)=7n+1根,令n=7可得答案.
解:∵图案①需火柴棒:8根;
图案②需火柴棒:8+7=15根;
图案③需火柴棒:8+7+7=22根;
…
∴图案n需火柴棒:8+7(n 1)=7n+1根;
当n=7时,7n+1=7×7+1=50,
∴图案⑦需50根火柴棒,
故选C.
此题主要考查了图形的变化类,解决此类题目的关键在于准确的找出图形在变化过程中不变的部分和变化的部分,变化部分是以何种规律变化.
7.B【解析】由图可知:●○○●●○○○○○每10个图形一循环,然后每组循环组里面有3个实心球,从而确定在2004个球中一共有多少个循环组,进一步得出答案即可.
解:∵●○○●●○○○○○每10个球一循环且每组循环组里面有3个实心球
∴2004÷10=200…4,第2004个是实心球,
则共有实现球200×3+1=601个.
故选:B.
此题考查图形的变化规律,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,找出循环的规律解决问题.
8.B【解析】由图可知,每个灰色正方形地砖右侧都有两个与之相邻的三角形地砖,而在整个步道的两侧尽头一共有4个三角形地砖,据此求解即可.
解:由图可知,每个灰色正方形地砖右侧都有两个与之相邻的三角形地砖,而在整个步道的两侧尽头一共有4个三角形地砖,
∴该步道上使用的三角形地砖数可表示为,
故选B.
本题主要考查了图形类的规律,正确理解题意找到规律是解题的关键.
9.C【解析】根据长方形窗框的横条长度求出长方形窗框的竖条长度,再根据长方形的面积公式计算即可求解.
解:∵长方形窗框的横条长度为m
∴长方形窗框的竖条长度为m
∴长方形窗框的面积为:m2
故选C.
本题考查了列代数式,要注意长方形窗框的横条有3条,观察图形求出长方形窗框的竖条长度是解答本题的关键.
10.B【解析】分别求出每一个图形的木棒数,然后再找出一般规律求解即可.
解:第1个图形共有7=1×(1+3)+3根木棒,
第2个图形共有13=2×(2+3)+3根木棒,
第3个图形共有21=3×(3+3)+3根木棒,
第4个图形共有31=4×(4+3)+3根木棒,
…
第n个图形共有n×(n+3)+3根木棒,
第11个图形共有11×(11+3)+3=157根木棒,
故选:B
此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.
11.C【解析】根据题意,一组数:、、、、、的和为250+251+252+…+299+2100==a+(2+22+…+250)a,进而根据所给等式的规律,可以发现2+22+…+250=251-2,由此即可求得答案.
250+251+252+…+299+2100
=a+2a+22a+…+250a
=a+(2+22+…+250)a,
∵,
,
,
…,
∴2+22+…+250=251-2,
∴250+251+252+…+299+2100
=a+(2+22+…+250)a
=a+(251-2)a
=a+(2 a-2)a
=2a2-a ,
故选C.
本题考查了规律题——数字的变化类,仔细观察,发现其中哪些发生了变化,哪些没有发生变化,是按什么规律变化的是解题的关键.
12.B【解析】由题意得出每行的数字之和等于2的序数减一次幂,据此解答即可.
∵第1行数字之和1=20,
第2行数字之和2=21,
第3行数字之和4=22,
第4行数字之和8=23,
…
∴第n行中所有数字之和为2n﹣1.
故选:B.
本题主要考查数字的变化类,解题的关键是每行的数相加,分析总结得出规律,根据规律求出第n行的数据之和.
13.D由题意设被截去部分为5n+2+1=5n+3
从其选项中看,故选D.
14.【解析】根据二次根式的定义,即可求解.
解:单项式的系数是.
故答案为:
本题主要考查了单项式的系数和次数的定义,熟练掌握单项式中的数字因式是单项式的系数,所有字母的和是单项式的次数是解题的关键.
15. 2【解析】根据单项式的系数定义“是指单项式中的数字因数”、次数的定义“是指所有字母的指数的和”即可得.
由单项式的系数与次数定义得:单项式的系数是,次数是
故答案为:,2.
本题考查了单项式的相关概念,熟记概念是解题关键.
16.(t-5)【解析】根据题意列出运算式子即可得.
由题意得:.
故答案为:.
本题考查了有理数减法的实际应用,依据题意,正确列出运算式子是解题关键.
17. 【解析】根据题意可知,只含字母a、b且单项式次数为4,可分三种情况:字母a的为3次,b为1次;字母a的为2次,b为2次;字母a的为1次,b为3次;由此即可作答.
单项式的次数是指单项式中所有字母因数的指数和,此题符合条件的不同类型的单项式可以是,,.
故答案为:,,.
本题主要考查了单项式次数的概念,解题的关键是掌握单项式的次数.
18.##【解析】观察发现,分子的规律:分子是常数1;分母的规律:第奇数项的分母为:,第偶数项的分母为:,据此写出第2021个数
分子的规律:分子是常数1;
分母的规律:第1个数的分母为:,
第2个数的分母为:,
第3个数的分母为:,
第4个数的分母为:,
第5个数的分母为:,
第6个数的分母为:,
…第奇数项的分母为:,第偶数项的分母为:,
所以第2021个数是
故答案为:
本题考查了数字类规律题,找到规律是解题的关键.
19.5【解析】根据程序计算多次,寻找出其中的规律,从第三次开始,出现1,5循环,计算(2022-2)÷2,确定余数,判断即可.
当k=125时,
第1次输出结果为,
第2次输出结果为,
第3次输出结果为,
第4次输出结果为,
第5次输出结果为,
第6次输出结果为,
从第三次开始,出现1,5循环,且奇数次为1,偶数次为为5,
∴第2022次输出的结果是5,
故答案为:5.
本题考查了有理数的混合运算,有理数中的规律,熟练计算,规范寻找循环节,确定变化规律是解题的关键.
20.(1)①(90+a);②(10+a);③(100-2a);(2)销售员甲与销售员乙的说法都正确,理由见解析【解析】(1)①根据题意,即可求出涨价后,每个玩具的销售价;
②根据题意,即可求出涨价后,每个玩具的利润;
③根据“销售价每涨价元时,其销售量将减少2个”,即可求出涨价后,玩具的月销售量;
(2)根据题意,分别求出上涨30元和上涨10元后每月的销售利润,即可判断.
解:(1)①根据题意,涨价后,每个玩具的销售价为(90+a)元
故答案为:(90+a);
②根据题意,涨价后,每个玩具的利润为90+a-80=(10+a)元
故答案为:(10+a);
③根据题意,涨价后,玩具的月销售量为(100-2a)元
故答案为:(100-2a);
(2)销售员甲与销售员乙的说法都正确,理由如下
若上涨30元,每月的销售利润为(90+30-80)×(100-30×2)=1600元
故甲正确;
若上涨10元,每月的销售利润为(90+10-80)×(100-10×2)=1600元
故乙正确.
故销售员甲与销售员乙的说法都正确.
此题考查的是列代数式表示实际意义,掌握实际问题中的各个量之间的关系是解决此题的关键.
21.(1)2个铁环组成的链条长6.8cm,3个铁环组成的链条长为9.6cm,4个铁环组成的链条长12.4cm
(2)y=2.8n+1.2
(3)需要51个铁环
【解析】根据观察,i链条每一个连处重合的部分是两个铁环的直径,根据题意列出算式求解即可.
(1)
由题意可得:4×2-0.6×2=6.8cm,4×3-0.6×4=9.6cm,4×4-0.6×6=12.4cm.
故2个铁环组成的链条长6.8cm,3个铁环组成的链条长为9.6cm,4个铁环组成的链条长12.4cm;
(2)
y=4n-2(n-1)×0.6,即y=2.8n+1.2;
(3)
1.44米=144cm据题意有2.8n+1.2=144,解得:n=51,
答:需要51个铁环.
本题主要考查了有理数的计算和用字母表示数,准确得根据题目和图形找出等量关系列出代数式是解题的关键.
22.(12R2+3πR2+2πr2)cm3【解析】先分别计算每个几何体体积,再相加.
解:由题意得:体积V=(2R)2×3+πR2×3+πr2×2
=(12R2+3πR2+2πr2)cm3.
答:该几何体的体积是(12R2+3πR2+2πr2)cm3.
本题考查几何体体积的计算,掌握各个几何体体积计算公式是求解本题的关键.
23.(1)应收水费36元
(2)应收水费为(4m-16)元
(3)一共要交128元或(184-3.5n)元
【解析】(1)利用用水量的范围计算结果即可;
(2)根据m的取值范围,先计算超过16立方米的费用,超过16立方米的用水量为(m﹣16)立方米,根据费用可计算结果;
(3)根据题意可列出5月份用水量的代数式,分情况讨论,若5月份用水(40﹣n)立方米不超过24立方米,根据题意列代数式计算5、6月份水费即可,若5月份用水(40﹣n)立方米超过24立方米,根据题意列代数式计算5、6月份水费即可,注意计算6月份用水量的范围.
(1)解:12×3=36(元);答:某居民2月份用水12立方米,应收水费36元;
(2)解:应收水费,16×3+(m-16)×4=4m-16(元).答:某户居民4月份应收水费为(4m-16)元
(3)解:6月份用水n立方米,则5月份用水(40-n)立方米,①若5月份用水(40-n)立方米不超过24立方米,则5月份水费为16×3+(40-n-16)×4=(144-4n)(元),因为16<40-n≤24,所以16≤n<24,则6月份水费为16×3+(n-16)×4=(4n-16)(元),所以5、6月份水费合计:(144-4n)+(4n-16)=128(元);②若5月份用水(40-n)立方米超过24立方米,则5月份水费为16×3+8×4+(40-n-24)×6.5=(184-6.5n)(元),因为40-n>24,所以n<16,则6月份水费为n×3=3n(元)所以5、6月份水费合计:(184-6.5n)+3n=(184-3.5n)(元);答:5、6月份水费一共要交128元或 (184-3.5n)元.
本题主要考查列代数式,找出题目蕴含的数量关系是解决问题的关键.
24.(1)39; 2n-1;(2) n2;(3)n2+n【解析】(1)由所给的数字可得第n个数为2n﹣1,据此解答即可;
(2)对所给的图形进行分析,总结出规律即可;
(3)利用(2)的方式进行求解即可.
解:(1)∵一列数1、3、5、7…,
∴第n个数为:2n﹣1,
∴第20个数为:2×20﹣1=39,
故答案为:39,2n﹣1;
(2)第(2)图中,分层小正方形的个数是(1+3)个,而整体计算小正方形的个数是22,所以,1+3=22;
第(3)图中,分层小正方形的个数是(1+3+5)个,而整体计算小正方形的个数是32,所以,1+3+5=32;
第(4)图中,分层小正方形的个数是(1+3+5+7)个,而整体计算小正方形的个数是42,所以,1+3+5+7=42;
猜测1+3+5+7+…+(2n﹣1)=n2;
(3)2+4+6+8+…+2n
=1+1+3+1+5+1+7+1+…+(2n﹣1)+1
=1+3+5+7+…+(2n﹣1)+n
=n2+n.
本题主要考查数字的变化规律,解答的关键是由所给的数字分析清楚存在的规律.
