人教A版选择性必修第一册1.1.2 空间向量的数量积运算 同步练习(Word版,含解析)
文档属性
| 名称 | 人教A版选择性必修第一册1.1.2 空间向量的数量积运算 同步练习(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 160.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 09:26:32 | ||
图片预览



文档简介
1.1.2 空间向量的数量积运算
基础过关练
题组一 数量积的概念及其运算
1.已知a=3p-2q,b=p+q,p和q是空间中相互垂直的单位向量,则a·b=( )
A.1 B.2 C.3 D.4
2.(2022福建三明一中开学考试)在三棱锥A-BCD中,AB=AC=AD=2,∠BAD=90°,∠BAC=60°,则·等于( )
A.-2 B.2
C.-2
3.已知|a|=4,|b|=8,a与b的夹角是120°,当a+2b与ka-b的夹角为钝角时,k的取值范围为 .
题组二 利用空间向量的数量积求夹角
4.(2021河北张家口尚义第一中学期中)已知e1,e2是夹角为60°的两个单位向量,则a=e1+e2与b=e1-2e2的夹角是( )
A.120° B.60°
C.30° D.45°
5.(2020贵州铜仁一中开学考试)已知两条异面直线的方向向量分别为a,b,且|a|=|b|=1,a·b=-,则两直线的夹角为( )
A.30° B.60°
C.120° D.150°
6.(2021天津西青期末)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P是C1D1的中点,则·= ,B1C与A1P所成角的大小为 .
题组三 利用空间向量的数量积求长度(模)
7.(2021黑龙江双鸭山一中期末)已知|a|=2,|b|=3,=60°,则|2a-3b|等于( )
A. D.61
8.(2021辽宁朝阳第一高级中学期中)在底面是正方形的四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,∠A1AD=∠A1AB=,则||=( )
A.2
题组四 利用空间向量的数量积解决垂直问题
9.已知|a|=3,|b|=4,m=a+b,n=a+λb,=135°,m⊥n,则λ= .
10.(2020广西柳州高级中学期中)如图所示,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC=DA=2,E为BC的中点.
(1)证明:AE⊥BC;
(2)求直线AE与DC所成角的余弦值.
能力提升练
题组一 利用空间向量的数量积求异面直线所成角(或余弦值)
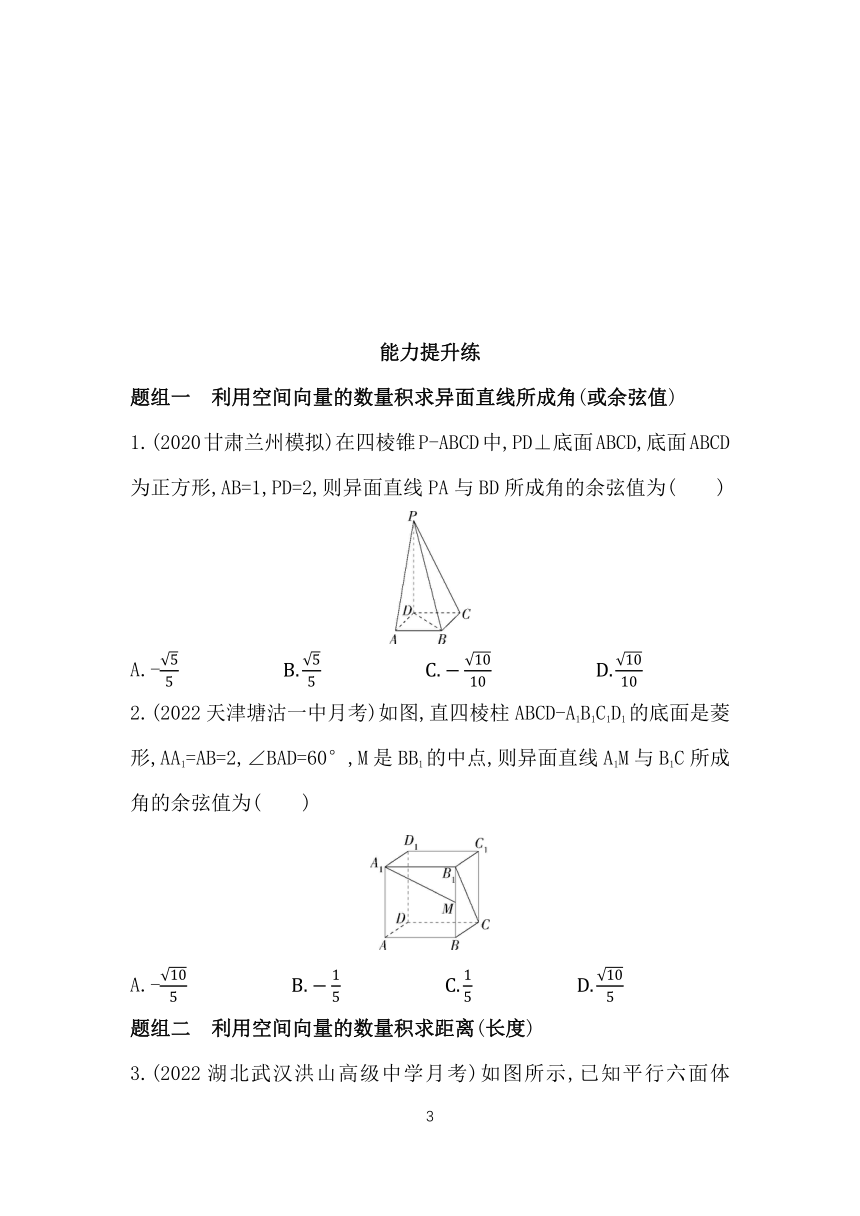
1.(2020甘肃兰州模拟)在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,AB=1,PD=2,则异面直线PA与BD所成角的余弦值为( )
A.-
2.(2022天津塘沽一中月考)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=AB=2,∠BAD=60°,M是BB1的中点,则异面直线A1M与B1C所成角的余弦值为( )
A.-
题组二 利用空间向量的数量积求距离(长度)
3.(2022湖北武汉洪山高级中学月考)如图所示,已知平行六面体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,∠BAA1=∠DAA1=∠BAD=60°,M为CC1的中点,则AM的长度为 .
4.(2022安徽合肥六中月考)如图所示,在平面角为120°的二面角α-AB-β中,AC α,BD β,且AC⊥AB,BD⊥AB,垂足分别为A,B,AC=AB=BD=6,则C,D间的距离为 .
题组三 利用空间向量的数量积证明垂直
5.(2020上海复旦大学附属中学期中)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥DC,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥PD;
(2)若F为棱PC上一点,满足BF⊥AC,求线段PF的长.
答案全解全析
基础过关练
1.A ∵p⊥q且|p|=|q|=1,∴a·b=(3p-2q)·(p+q)=3p2+p·
q-2q2=3+0-2=1.
2.A ·=·(-)=·-·=0-2×2×cos60°
=-2.
3.答案 k>-7且k≠-
解析 由题意得(a+2b)·(ka-b)=ka2+(2k-1)a·b-2b2=16k+
(2k-1)×4×8×cos120°-128=-16k-112<0,解得k>-7.
又当k=-时,a+2b与ka-b反向共线,
∴k>-7且k≠-.
名师点睛
两向量a,b的夹角为锐角时,a·b>0,但a·b>0时,a,b的夹角为锐角或零角;两向量a,b的夹角为钝角时,a·b<0,但a·b<0时,a,b的夹角为钝角或平角.故在实际解题中,要考虑两向量同向、反向的情形.
4.A 由题意得a·b=(e1+e2)·(e1-2e2)=-e1·e2-2=1-1×1×
-2=-,|a|=====,
|b|=====.
∴cos===-.∴=120°.
5.B 设向量a,b的夹角为θ,则cosθ==-,∴θ=120°,∴两个方向向量对应的直线的夹角为180°-120°=60°.故选B.
易错警示
异面直线所成的角θ的取值范围为0°<θ≤90°,故此题中异面直线所成的角应为120°的补角.
6.答案 1;60°
解析 解法一:·=(+)·==1.
由题意可得PA1=B1C=,所以cos<,>==,所以<,>=60°.
解法二:连接A1D,PD,则∠PA1D(或其补角)就是B1C与A1P所成的角.在△PA1D中,易得PA1=DA1=PD=,故△PA1D为等边三角形,从而∠PA1D=60°,即B1C与A1P所成角的大小为60°.所以·=××cos60°=1.
7.C |2a-3b|2=4a2-12a·b+9b2=4×22-12×2×3×cos60°+9×32=
61,∴|2a-3b|=.
8.D ||2=|++|2=||2+||2+||2+2·+2
·+2·=12+12+22+2×1×1×cos+2×1×2×cos+2×1×2×cos=1+1+4+2+2=10,∴||=.故选D.
9.答案 -
解析 由m⊥n,得(a+b)·(a+λb)=0,∴a2+(1+λ)a·b+λb2=0,
∴18+(λ+1)×3×4cos135°+16λ=0,即2λ+3=0,∴λ=-.
10.解析 (1)证明:连接DE,则=-=(+)-,=
-,所以·=·(-)=·
-·+·-·-·+·=0-2+2-0-0+0=0,所以AE⊥BC.
(2)·=·=·+·-·
=0+2-0=2,||==,
所以cos<,>===,
即直线AE与DC所成角的余弦值为.
能力提升练
1.D ∵PD⊥平面ABCD,DA,DC 平面ABCD,
∴PD⊥DA,PD⊥DC.
∵底面ABCD为正方形,∴DA⊥DC.
易知=-,=+,
∴·=(-)·(+)=+·-·-·=1,
||====,
||====,
∴|cos<,>|===,
∴异面直线PA与BD所成角的余弦值为.
2.D 由题意可得=+=-,=-,||=
,||=2,∴·=·(-)=·+=2×2×cos60°+×4=4.∴cos<,>==.
∴异面直线A1M与B1C所成角的余弦值为.故选D.
3.答案 2
解析 ∵=++,
∴||2==||2+||2+||2+2·+
·+·=22+22+×42+2×2×2×+4×2×+2×4×=24,
∴||=2.
4.答案 12
解析 ∵AC⊥AB,BD⊥AB,
∴·=0,·=0.
∵二面角α-AB-β的平面角为120°,
∴<,>=180°-120°=60°.
∴=(++)2=+++2·+2·+2·=3×62+2×62×cos60°=144,
∴CD=12.
5.解析 (1)证明:∵E为PC的中点,∴=(+)=(-+
-)=(+-)=(+),又=-,
∴·=(-)=0,∴BE⊥PD.
(2)∵F为PC上一点,
∴设=λ(0≤λ≤1),
∴=+=-+λ=-+λ(+2-)=(1-λ)-
(1-2λ)+λ.
又BF⊥AC,
∴·=[(1-λ)-(1-2λ)+λ]·(+2)=-2(1-2λ)+4λ=0,解得λ=.
易知||===2,
∴PF=PC=,即线段PF的长为.
9
基础过关练
题组一 数量积的概念及其运算
1.已知a=3p-2q,b=p+q,p和q是空间中相互垂直的单位向量,则a·b=( )
A.1 B.2 C.3 D.4
2.(2022福建三明一中开学考试)在三棱锥A-BCD中,AB=AC=AD=2,∠BAD=90°,∠BAC=60°,则·等于( )
A.-2 B.2
C.-2
3.已知|a|=4,|b|=8,a与b的夹角是120°,当a+2b与ka-b的夹角为钝角时,k的取值范围为 .
题组二 利用空间向量的数量积求夹角
4.(2021河北张家口尚义第一中学期中)已知e1,e2是夹角为60°的两个单位向量,则a=e1+e2与b=e1-2e2的夹角是( )
A.120° B.60°
C.30° D.45°
5.(2020贵州铜仁一中开学考试)已知两条异面直线的方向向量分别为a,b,且|a|=|b|=1,a·b=-,则两直线的夹角为( )
A.30° B.60°
C.120° D.150°
6.(2021天津西青期末)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P是C1D1的中点,则·= ,B1C与A1P所成角的大小为 .
题组三 利用空间向量的数量积求长度(模)
7.(2021黑龙江双鸭山一中期末)已知|a|=2,|b|=3,
A. D.61
8.(2021辽宁朝阳第一高级中学期中)在底面是正方形的四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,∠A1AD=∠A1AB=,则||=( )
A.2
题组四 利用空间向量的数量积解决垂直问题
9.已知|a|=3,|b|=4,m=a+b,n=a+λb,
10.(2020广西柳州高级中学期中)如图所示,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC=DA=2,E为BC的中点.
(1)证明:AE⊥BC;
(2)求直线AE与DC所成角的余弦值.
能力提升练
题组一 利用空间向量的数量积求异面直线所成角(或余弦值)
1.(2020甘肃兰州模拟)在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,AB=1,PD=2,则异面直线PA与BD所成角的余弦值为( )
A.-
2.(2022天津塘沽一中月考)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=AB=2,∠BAD=60°,M是BB1的中点,则异面直线A1M与B1C所成角的余弦值为( )
A.-
题组二 利用空间向量的数量积求距离(长度)
3.(2022湖北武汉洪山高级中学月考)如图所示,已知平行六面体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,∠BAA1=∠DAA1=∠BAD=60°,M为CC1的中点,则AM的长度为 .
4.(2022安徽合肥六中月考)如图所示,在平面角为120°的二面角α-AB-β中,AC α,BD β,且AC⊥AB,BD⊥AB,垂足分别为A,B,AC=AB=BD=6,则C,D间的距离为 .
题组三 利用空间向量的数量积证明垂直
5.(2020上海复旦大学附属中学期中)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥DC,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥PD;
(2)若F为棱PC上一点,满足BF⊥AC,求线段PF的长.
答案全解全析
基础过关练
1.A ∵p⊥q且|p|=|q|=1,∴a·b=(3p-2q)·(p+q)=3p2+p·
q-2q2=3+0-2=1.
2.A ·=·(-)=·-·=0-2×2×cos60°
=-2.
3.答案 k>-7且k≠-
解析 由题意得(a+2b)·(ka-b)=ka2+(2k-1)a·b-2b2=16k+
(2k-1)×4×8×cos120°-128=-16k-112<0,解得k>-7.
又当k=-时,a+2b与ka-b反向共线,
∴k>-7且k≠-.
名师点睛
两向量a,b的夹角为锐角时,a·b>0,但a·b>0时,a,b的夹角为锐角或零角;两向量a,b的夹角为钝角时,a·b<0,但a·b<0时,a,b的夹角为钝角或平角.故在实际解题中,要考虑两向量同向、反向的情形.
4.A 由题意得a·b=(e1+e2)·(e1-2e2)=-e1·e2-2=1-1×1×
-2=-,|a|=====,
|b|=====.
∴cos
5.B 设向量a,b的夹角为θ,则cosθ==-,∴θ=120°,∴两个方向向量对应的直线的夹角为180°-120°=60°.故选B.
易错警示
异面直线所成的角θ的取值范围为0°<θ≤90°,故此题中异面直线所成的角应为120°的补角.
6.答案 1;60°
解析 解法一:·=(+)·==1.
由题意可得PA1=B1C=,所以cos<,>==,所以<,>=60°.
解法二:连接A1D,PD,则∠PA1D(或其补角)就是B1C与A1P所成的角.在△PA1D中,易得PA1=DA1=PD=,故△PA1D为等边三角形,从而∠PA1D=60°,即B1C与A1P所成角的大小为60°.所以·=××cos60°=1.
7.C |2a-3b|2=4a2-12a·b+9b2=4×22-12×2×3×cos60°+9×32=
61,∴|2a-3b|=.
8.D ||2=|++|2=||2+||2+||2+2·+2
·+2·=12+12+22+2×1×1×cos+2×1×2×cos+2×1×2×cos=1+1+4+2+2=10,∴||=.故选D.
9.答案 -
解析 由m⊥n,得(a+b)·(a+λb)=0,∴a2+(1+λ)a·b+λb2=0,
∴18+(λ+1)×3×4cos135°+16λ=0,即2λ+3=0,∴λ=-.
10.解析 (1)证明:连接DE,则=-=(+)-,=
-,所以·=·(-)=·
-·+·-·-·+·=0-2+2-0-0+0=0,所以AE⊥BC.
(2)·=·=·+·-·
=0+2-0=2,||==,
所以cos<,>===,
即直线AE与DC所成角的余弦值为.
能力提升练
1.D ∵PD⊥平面ABCD,DA,DC 平面ABCD,
∴PD⊥DA,PD⊥DC.
∵底面ABCD为正方形,∴DA⊥DC.
易知=-,=+,
∴·=(-)·(+)=+·-·-·=1,
||====,
||====,
∴|cos<,>|===,
∴异面直线PA与BD所成角的余弦值为.
2.D 由题意可得=+=-,=-,||=
,||=2,∴·=·(-)=·+=2×2×cos60°+×4=4.∴cos<,>==.
∴异面直线A1M与B1C所成角的余弦值为.故选D.
3.答案 2
解析 ∵=++,
∴||2==||2+||2+||2+2·+
·+·=22+22+×42+2×2×2×+4×2×+2×4×=24,
∴||=2.
4.答案 12
解析 ∵AC⊥AB,BD⊥AB,
∴·=0,·=0.
∵二面角α-AB-β的平面角为120°,
∴<,>=180°-120°=60°.
∴=(++)2=+++2·+2·+2·=3×62+2×62×cos60°=144,
∴CD=12.
5.解析 (1)证明:∵E为PC的中点,∴=(+)=(-+
-)=(+-)=(+),又=-,
∴·=(-)=0,∴BE⊥PD.
(2)∵F为PC上一点,
∴设=λ(0≤λ≤1),
∴=+=-+λ=-+λ(+2-)=(1-λ)-
(1-2λ)+λ.
又BF⊥AC,
∴·=[(1-λ)-(1-2λ)+λ]·(+2)=-2(1-2λ)+4λ=0,解得λ=.
易知||===2,
∴PF=PC=,即线段PF的长为.
9
