人教A版选择性必修第一册 2.1.1 倾斜角与斜率同步练习(Word含答案)
文档属性
| 名称 | 人教A版选择性必修第一册 2.1.1 倾斜角与斜率同步练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 143.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 17:34:23 | ||
图片预览




文档简介
第二章 直线和圆的方程
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
基础过关练
题组一 直线的倾斜角与斜率
1.(多选)下列说法中正确的是( )
A.任何一条直线都有唯一的倾斜角
B.若两直线的倾斜角相等,则它们的斜率也一定相等
C.若一条直线的斜率为tanα,则此直线的倾斜角为α
D.直线的倾斜角的取值范围是[0,π)
2.(2022北京贸大附中质检)已知直线l的倾斜角为α-15°,则下列结论中正确的是( )
A.0°≤α<180° B.15°<α<180°
C.15°≤α<180° D.15°≤α<195°
3.直线l的倾斜角是斜率为的直线的倾斜角的2倍,则l的斜率为( )
A.1 B.
4.(2022福建龙岩长汀龙宇中学期中)如图,直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
A.k1C.k35.(2022辽宁沈阳二中段考)已知直线l的斜率为k,倾斜角为α,若45°<α<135°,则k的取值范围为( )
A.(-1,1)
B.(-∞,-1)∪(1,+∞)
C.[-1,1]
D.(-∞,-1]∪[1,+∞)
6.(2022山东东营一中月考)设直线l的斜率为k,且-1≤k<,则直线l的倾斜角α的取值范围为( )
A.
C.
题组二 直线的斜率公式及应用
7.(2022吉林长春外国语学校月考)若直线l经过原点和(-1,1),则直线l的斜率为( )
A.0 B.1 C.-1 D.不存在
8.(2021安徽亳州二中期末)已知三点A(-1,1),B(0,2),C(2,x),若A,B,C三点共线,则x的值为( )
A.2 B.-2 C.4 D.-4
9.已知点A(2,-1),若在坐标轴上存在一点P,使直线PA的倾斜角为45°,则点P的坐标为 .
10.(2022山东菏泽一中月考)已知直线l的一个方向向量为d=(3,-4),则直线l的斜率为 .
11.(2022江苏南京三校联考)若A(3,1),B(-2,k),C(8,1)三点能构成三角形,则实数k的取值范围为 .
能力提升练
题组一 直线的倾斜角与斜率
1.(2021湖南长沙雅礼中学期末)若直线l经过A(2,1),B(1,-m2)
(m∈R)两点,则直线l的倾斜角α的取值范围是( )
A.0≤α≤<α<π
C.
2.(2022天津新华中学月考)过点A(2,1),B(m,3)的直线的倾斜角α的取值范围是,则实数m的取值范围是( )
A.(0,2] B.(0,4)
C.[2,4) D.(0,2)∪(2,4)
3.(2021黑龙江哈尔滨六中开学考试)直线l过点A(1,2),且不经过第四象限,则直线l的斜率的取值范围为 .
题组二 直线斜率的综合运用
4.(2022辽宁葫芦岛检测)王老师在课堂上与学生探究直线时,有四位同学分别给出了一个结论.甲:直线经过点(1,2).乙:直线经过点(3,9).丙:直线经过点(0,-1).丁:直线的斜率为整数.如果只有一位同学的结论是错误的,那么这位同学是( )
A.甲 B.乙 C.丙 D.丁
5.(2022浙江台州椒江书生中学月考)已知A(2,3),B(-1,2),若点P(x,y)在线段AB上,则的最大值为( )
A.1 B. D.-3
6.(2021安徽六安一中期末)如图,在矩形ABCD中,BC=AB,直线AC的斜率为,则直线BC的斜率为( )
A.
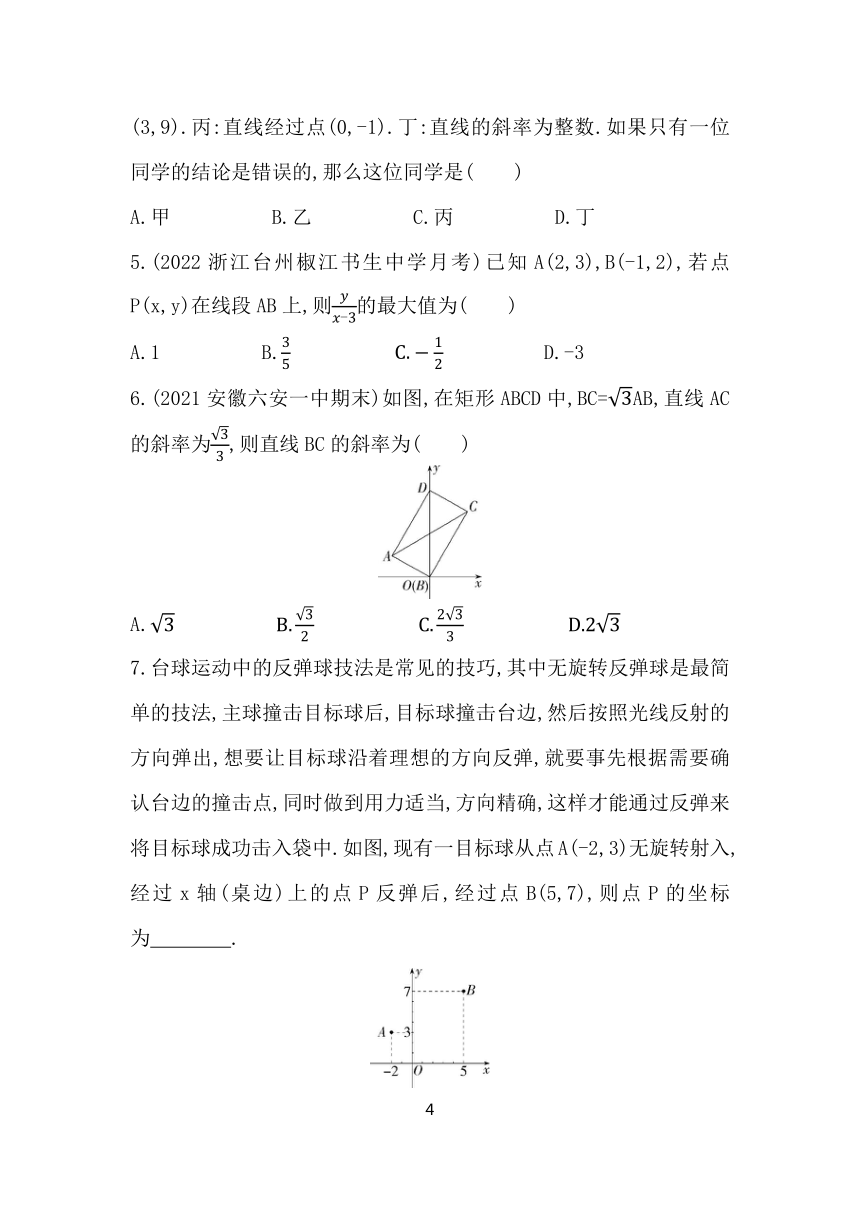
7.台球运动中的反弹球技法是常见的技巧,其中无旋转反弹球是最简单的技法,主球撞击目标球后,目标球撞击台边,然后按照光线反射的方向弹出,想要让目标球沿着理想的方向反弹,就要事先根据需要确认台边的撞击点,同时做到用力适当,方向精确,这样才能通过反弹来将目标球成功击入袋中.如图,现有一目标球从点A(-2,3)无旋转射入,经过x轴(桌边)上的点P反弹后,经过点B(5,7),则点P的坐标为 .
8.(2022辽宁沈阳八十三中期初)已知A(3,3),B(-4,2),C(0,-2).
(1)求直线AB的斜率并写出直线BC的一个方向向量;
(2)若点D在线段BC(包括端点)上移动,求直线AD的斜率的变化范围.
答案全解全析
基础过关练
1.AD A、D显然对;若两直线的倾斜角为90°,则它们的斜率不存在,故B错误;若一条直线的斜率为tan(-60°)=-,则此直线的倾斜角为120°,故C错误.
2.D ∵直线的倾斜角θ的取值范围是0°≤θ<180°,∴0°≤α-
15°<180°,解得15°≤α<195°.故选D.
3.B 易知斜率为的直线的倾斜角为30°,
∴直线l的倾斜角为60°,
∴直线l的斜率为tan60°=.故选B.
易错警示
倍数关系指的是倾斜角而不是斜率.
4.D 由题图可知,直线l1的倾斜角为钝角,所以k1<0;直线l2与直线l3的倾斜角为锐角,且直线l2的倾斜角较大,所以k2>k3>0,所以k2>k3>k1.
5.B 由45°<α<135°可知,k>tan45°=1或k6.D 由-1≤k<,得-1≤tanα<,
又α∈[0,π),
∴α∈∪.
故选D.
7.C 直线l的斜率为=-1.故选C.
8.C 由题意得kAB==1.因为A,B,C三点共线,所以kAB=kBC,即=1,解得x=4.故选C.
规律方法 用斜率解决三点共线的方法
9.答案 (3,0)或(0,-3)
解析 设点P的坐标为(x,0),则=tan45°=1,解得x=3,即P(3,0).
设点P的坐标为(0,y),则=tan45°=1,解得y=-3,即P(0,-3).
综上,点P的坐标为(3,0)或(0,-3).
10.答案 -
解析 设直线l的斜率为k,则直线l的一个方向向量n=(1,k).又直线l的一个方向向量为d=(3,-4),∴n∥d,即1×(-4)-3k=0,解得k=-.
11.答案 k≠1
解析 由于A,B,C三点能构成三角形,故kAB≠kAC,即≠,解得k≠1.
能力提升练
1.C 由题意可知直线l的斜率k==1+m2≥1,即tanα≥1,又因为0≤α<π,所以≤α<.故选C.
2.B 当直线的倾斜角α的取值范围是∪时,直线的斜率k的取值范围是(-∞,-1)∪(1,+∞),即<-1或>1,解得0综上,实数m的取值范围是(0,4).故选B.
易错警示
已知倾斜角的取值范围确定斜率的范围时,要注意倾斜角的取值范围中是否含有90°的情况,若有,斜率的范围需分成两段.
3.答案 [0,2]
解析 当直线l的倾斜角为0°时,斜率为0;
当直线经过原点时,斜率为2.
∵直线l过点A(1,2),且不经过第四象限,
∴直线l的斜率的取值范围为[0,2].
4.B 假设甲同学的结论错误,则乙、丙、丁同学的结论正确,由乙、丙同学的结论正确可知直线的斜率k==,此时丁同学的结论不正确,故假设不成立.同理,可知乙同学的结论是错误的.故选B.
5.C 表示过点P(x,y)与点(3,0)的直线的斜率.记点(3,0)为C,则kAC==-3,kBC==-.因为点P在线段AB上,所以-3≤≤-,则的最大值为-.故选C.
6.A 在Rt△ABC中,∠ABC=,BC=AB,所以tan∠ACB==,即∠ACB=.设直线AC的倾斜角为θ,则tanθ=,直线BC的倾斜角为θ+,故kBC=tan==.故选A.
7.答案
信息提取 ①目标球从A(-2,3)无旋转射入;②经过x轴(桌边)上的点反弹后,经过B(5,7).
数学建模 将台球中的无旋转反弹问题转化为光线的反射问题,运用的知识是①点关于线对称,求A点关于x轴的对称点A'或B点关于x轴的对称点B';②三点共线,即A',P,B三点共线或A,P,B'三点共线.再用所学公式解决问题.
解析 设P(x,0).易知A点关于x轴对称的点A'的坐标为(-2,-3),则kA'P==,kA'B==.
∵A',B,P三点共线,∴kA'P=kA'B,即=,解得x=,
故点P的坐标为.
解题模板
求解光线的反射问题通常用到对称的知识,若A点向P点反射至B点,则A点的对称点A'与P,B共线,此直线为反射线;B点的对称点B'与P,A共线,此直线为入射线.
8.解析 (1)kAB==,kBC==-1,
∴直线BC的一个方向向量为(1,-1).
(2)如图,当点D由点B运动到点C时,直线AD的斜率由kAB增大到kAC.
易知kAB=,kAC==,
∴直线AD的斜率的变化范围为.
10
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
基础过关练
题组一 直线的倾斜角与斜率
1.(多选)下列说法中正确的是( )
A.任何一条直线都有唯一的倾斜角
B.若两直线的倾斜角相等,则它们的斜率也一定相等
C.若一条直线的斜率为tanα,则此直线的倾斜角为α
D.直线的倾斜角的取值范围是[0,π)
2.(2022北京贸大附中质检)已知直线l的倾斜角为α-15°,则下列结论中正确的是( )
A.0°≤α<180° B.15°<α<180°
C.15°≤α<180° D.15°≤α<195°
3.直线l的倾斜角是斜率为的直线的倾斜角的2倍,则l的斜率为( )
A.1 B.
4.(2022福建龙岩长汀龙宇中学期中)如图,直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
A.k1
A.(-1,1)
B.(-∞,-1)∪(1,+∞)
C.[-1,1]
D.(-∞,-1]∪[1,+∞)
6.(2022山东东营一中月考)设直线l的斜率为k,且-1≤k<,则直线l的倾斜角α的取值范围为( )
A.
C.
题组二 直线的斜率公式及应用
7.(2022吉林长春外国语学校月考)若直线l经过原点和(-1,1),则直线l的斜率为( )
A.0 B.1 C.-1 D.不存在
8.(2021安徽亳州二中期末)已知三点A(-1,1),B(0,2),C(2,x),若A,B,C三点共线,则x的值为( )
A.2 B.-2 C.4 D.-4
9.已知点A(2,-1),若在坐标轴上存在一点P,使直线PA的倾斜角为45°,则点P的坐标为 .
10.(2022山东菏泽一中月考)已知直线l的一个方向向量为d=(3,-4),则直线l的斜率为 .
11.(2022江苏南京三校联考)若A(3,1),B(-2,k),C(8,1)三点能构成三角形,则实数k的取值范围为 .
能力提升练
题组一 直线的倾斜角与斜率
1.(2021湖南长沙雅礼中学期末)若直线l经过A(2,1),B(1,-m2)
(m∈R)两点,则直线l的倾斜角α的取值范围是( )
A.0≤α≤<α<π
C.
2.(2022天津新华中学月考)过点A(2,1),B(m,3)的直线的倾斜角α的取值范围是,则实数m的取值范围是( )
A.(0,2] B.(0,4)
C.[2,4) D.(0,2)∪(2,4)
3.(2021黑龙江哈尔滨六中开学考试)直线l过点A(1,2),且不经过第四象限,则直线l的斜率的取值范围为 .
题组二 直线斜率的综合运用
4.(2022辽宁葫芦岛检测)王老师在课堂上与学生探究直线时,有四位同学分别给出了一个结论.甲:直线经过点(1,2).乙:直线经过点(3,9).丙:直线经过点(0,-1).丁:直线的斜率为整数.如果只有一位同学的结论是错误的,那么这位同学是( )
A.甲 B.乙 C.丙 D.丁
5.(2022浙江台州椒江书生中学月考)已知A(2,3),B(-1,2),若点P(x,y)在线段AB上,则的最大值为( )
A.1 B. D.-3
6.(2021安徽六安一中期末)如图,在矩形ABCD中,BC=AB,直线AC的斜率为,则直线BC的斜率为( )
A.
7.台球运动中的反弹球技法是常见的技巧,其中无旋转反弹球是最简单的技法,主球撞击目标球后,目标球撞击台边,然后按照光线反射的方向弹出,想要让目标球沿着理想的方向反弹,就要事先根据需要确认台边的撞击点,同时做到用力适当,方向精确,这样才能通过反弹来将目标球成功击入袋中.如图,现有一目标球从点A(-2,3)无旋转射入,经过x轴(桌边)上的点P反弹后,经过点B(5,7),则点P的坐标为 .
8.(2022辽宁沈阳八十三中期初)已知A(3,3),B(-4,2),C(0,-2).
(1)求直线AB的斜率并写出直线BC的一个方向向量;
(2)若点D在线段BC(包括端点)上移动,求直线AD的斜率的变化范围.
答案全解全析
基础过关练
1.AD A、D显然对;若两直线的倾斜角为90°,则它们的斜率不存在,故B错误;若一条直线的斜率为tan(-60°)=-,则此直线的倾斜角为120°,故C错误.
2.D ∵直线的倾斜角θ的取值范围是0°≤θ<180°,∴0°≤α-
15°<180°,解得15°≤α<195°.故选D.
3.B 易知斜率为的直线的倾斜角为30°,
∴直线l的倾斜角为60°,
∴直线l的斜率为tan60°=.故选B.
易错警示
倍数关系指的是倾斜角而不是斜率.
4.D 由题图可知,直线l1的倾斜角为钝角,所以k1<0;直线l2与直线l3的倾斜角为锐角,且直线l2的倾斜角较大,所以k2>k3>0,所以k2>k3>k1.
5.B 由45°<α<135°可知,k>tan45°=1或k
又α∈[0,π),
∴α∈∪.
故选D.
7.C 直线l的斜率为=-1.故选C.
8.C 由题意得kAB==1.因为A,B,C三点共线,所以kAB=kBC,即=1,解得x=4.故选C.
规律方法 用斜率解决三点共线的方法
9.答案 (3,0)或(0,-3)
解析 设点P的坐标为(x,0),则=tan45°=1,解得x=3,即P(3,0).
设点P的坐标为(0,y),则=tan45°=1,解得y=-3,即P(0,-3).
综上,点P的坐标为(3,0)或(0,-3).
10.答案 -
解析 设直线l的斜率为k,则直线l的一个方向向量n=(1,k).又直线l的一个方向向量为d=(3,-4),∴n∥d,即1×(-4)-3k=0,解得k=-.
11.答案 k≠1
解析 由于A,B,C三点能构成三角形,故kAB≠kAC,即≠,解得k≠1.
能力提升练
1.C 由题意可知直线l的斜率k==1+m2≥1,即tanα≥1,又因为0≤α<π,所以≤α<.故选C.
2.B 当直线的倾斜角α的取值范围是∪时,直线的斜率k的取值范围是(-∞,-1)∪(1,+∞),即<-1或>1,解得0
易错警示
已知倾斜角的取值范围确定斜率的范围时,要注意倾斜角的取值范围中是否含有90°的情况,若有,斜率的范围需分成两段.
3.答案 [0,2]
解析 当直线l的倾斜角为0°时,斜率为0;
当直线经过原点时,斜率为2.
∵直线l过点A(1,2),且不经过第四象限,
∴直线l的斜率的取值范围为[0,2].
4.B 假设甲同学的结论错误,则乙、丙、丁同学的结论正确,由乙、丙同学的结论正确可知直线的斜率k==,此时丁同学的结论不正确,故假设不成立.同理,可知乙同学的结论是错误的.故选B.
5.C 表示过点P(x,y)与点(3,0)的直线的斜率.记点(3,0)为C,则kAC==-3,kBC==-.因为点P在线段AB上,所以-3≤≤-,则的最大值为-.故选C.
6.A 在Rt△ABC中,∠ABC=,BC=AB,所以tan∠ACB==,即∠ACB=.设直线AC的倾斜角为θ,则tanθ=,直线BC的倾斜角为θ+,故kBC=tan==.故选A.
7.答案
信息提取 ①目标球从A(-2,3)无旋转射入;②经过x轴(桌边)上的点反弹后,经过B(5,7).
数学建模 将台球中的无旋转反弹问题转化为光线的反射问题,运用的知识是①点关于线对称,求A点关于x轴的对称点A'或B点关于x轴的对称点B';②三点共线,即A',P,B三点共线或A,P,B'三点共线.再用所学公式解决问题.
解析 设P(x,0).易知A点关于x轴对称的点A'的坐标为(-2,-3),则kA'P==,kA'B==.
∵A',B,P三点共线,∴kA'P=kA'B,即=,解得x=,
故点P的坐标为.
解题模板
求解光线的反射问题通常用到对称的知识,若A点向P点反射至B点,则A点的对称点A'与P,B共线,此直线为反射线;B点的对称点B'与P,A共线,此直线为入射线.
8.解析 (1)kAB==,kBC==-1,
∴直线BC的一个方向向量为(1,-1).
(2)如图,当点D由点B运动到点C时,直线AD的斜率由kAB增大到kAC.
易知kAB=,kAC==,
∴直线AD的斜率的变化范围为.
10
