2022—2023学年人教版数学七年级上册3.4 实际问题与一元一次方程 课件(共14张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学七年级上册3.4 实际问题与一元一次方程 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 17:10:52 | ||
图片预览






文档简介
(共14张PPT)
3.4 实际问题与一元一次方程
配套问题
某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母。1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例 1
1
分析:
“每人每天可以生产1200个螺钉或2000个螺母”
这句话是什么意思?
2
思考:
“1个螺钉配2个螺母”包含了什么等量关系?
3
若设x名工人生产螺钉,那么 人生产螺母,生产螺钉的数量是 ,生产的螺母的数量是 .
审题
导入
配套问题
2
思考:“1个螺钉配2个螺母”这句话是什么意思?它包含了什么等量关系?
配套:
套数 螺钉数量 螺母数量
1 1 2
2 2 4
3 3 6
4 4 8
… … …
n n 2n
螺钉
螺母
知识讲解
列表分析:
产品类型 人数 单人产量 总产量
螺钉 x 1 200
螺母 2 000
×
=
1 200 x
×
=
2 000(22-x)
人数和为22人
(22﹣x)
1×螺母的数量 = 2×螺钉的数量
3
若设x名工人生产螺钉,那么 人生产螺母,生产螺钉的数量是 ,生产的螺母的数是 .
配套问题
2 000(22-x) = 2×1 200x
知识讲解
难点突破
配套问题
某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母。1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例 1
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
列方程 2 000(22-x) =2×1 200x.
解方程 5(22-x) =6x.
110-5x = 6x.
11x=110.
得 x=10
∴ 22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
知识讲解
配套问题(变式训练)
某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母。1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?若设应安排x名工人生产螺钉,你能列出方程吗?
练习
审题:
解:设应安排x名工人生产螺钉,(22-x)名工人生螺母 ,
列方程得
3×1200x=2×2000(22-x)
2个螺钉需要配3个螺母,
即: 3×螺钉总数量=2×螺母总数量
课堂练习
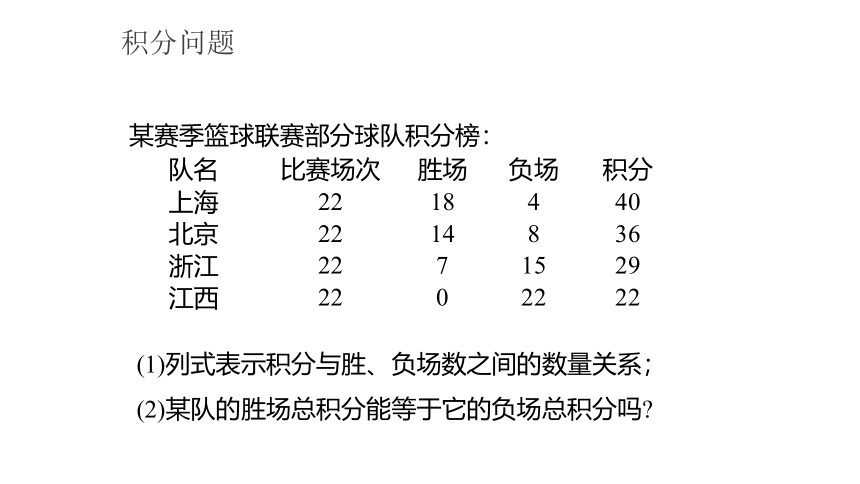
某赛季篮球联赛部分球队积分榜:
队名 比赛场次 胜场 负场 积分
上海 22 18 4 40
北京 22 14 8 36
浙江 22 7 15 29
江西 22 0 22 22
(1)列式表示积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗
积分问题
解:观察积分榜,从最下面一行可看出,负一场积1分.
设胜一场积x分根据表中其他任意一行可以列方程,求出x的值.例如,根据第一行可列方程:
18x+1×4=40.
由此得出 x=2.
用表中其他行可以验证,得出结论:负一场积1分,胜一场积2分.
(1)如果一个队胜m场,则负(22-m)场,胜场积分为2m,负场积分为22-m,总积分为
2m+(22-m)=m+22.
三、知识讲解
(2)设一个队胜了x场,则负了(22-x)场,如果这个队的胜场总积分等于负场总积分,则有方程
其中,x (胜场)的值必须是整数,所以 不符合实际意义. 由此可以判定没有哪个队伍的胜场总积分等于负场总积分.
考试竞赛得分问题
学校组织知识竞赛,共设20道选择题,各题分值相同,每题必答,下表记录的是5名参赛者的得分情况:
参赛者 A B C D
答对数 20 19 18 14
答错数 0 1 2 6
得分 100 94 88 64
E
10
10
40
(1)由表格知,答对一题得____分,答错一题得____分。
(2)参赛者F得82分,他答对了几道题
(3)参赛者G说他得90分,你认为可能吗?为什么?
5
-1
解:(2)设他答对了x道题,则答错了 (20-x)道题。
根据题意,得 2x+(20-x)=82.
解得 x=17.
答:他答对了17道题.
(3)不可能.理由:设参赛者G答对了m道题,则答错 (20-m)道题.
根据题意,得5m+(20-m)=90.解得m=
因为m为整数,所以不符合题意,故参赛者G不可能90分.
比赛积分问题:积分问题中常用比赛总场数及比赛总得分来找相等关系。
比赛总场数=胜场数+负场数
比赛总积分=胜场积分+负场积分+平场总分
考试竞赛问题:与比赛积分问题类似,其基本的相等关系为:
总题数=答对题数+答错题数+未答题数
总得分=答对得分+答错得分+未答得分
课堂小结
实际问题
实际问题的答案
一元一次方程
一元一次方程的解(x=a)
设未知数
列方程
解方程
检验
小结
这一过程一般包括以下几个步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并答话.
小结
3.4 实际问题与一元一次方程
配套问题
某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母。1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例 1
1
分析:
“每人每天可以生产1200个螺钉或2000个螺母”
这句话是什么意思?
2
思考:
“1个螺钉配2个螺母”包含了什么等量关系?
3
若设x名工人生产螺钉,那么 人生产螺母,生产螺钉的数量是 ,生产的螺母的数量是 .
审题
导入
配套问题
2
思考:“1个螺钉配2个螺母”这句话是什么意思?它包含了什么等量关系?
配套:
套数 螺钉数量 螺母数量
1 1 2
2 2 4
3 3 6
4 4 8
… … …
n n 2n
螺钉
螺母
知识讲解
列表分析:
产品类型 人数 单人产量 总产量
螺钉 x 1 200
螺母 2 000
×
=
1 200 x
×
=
2 000(22-x)
人数和为22人
(22﹣x)
1×螺母的数量 = 2×螺钉的数量
3
若设x名工人生产螺钉,那么 人生产螺母,生产螺钉的数量是 ,生产的螺母的数是 .
配套问题
2 000(22-x) = 2×1 200x
知识讲解
难点突破
配套问题
某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母。1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例 1
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
列方程 2 000(22-x) =2×1 200x.
解方程 5(22-x) =6x.
110-5x = 6x.
11x=110.
得 x=10
∴ 22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
知识讲解
配套问题(变式训练)
某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母。1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?若设应安排x名工人生产螺钉,你能列出方程吗?
练习
审题:
解:设应安排x名工人生产螺钉,(22-x)名工人生螺母 ,
列方程得
3×1200x=2×2000(22-x)
2个螺钉需要配3个螺母,
即: 3×螺钉总数量=2×螺母总数量
课堂练习
某赛季篮球联赛部分球队积分榜:
队名 比赛场次 胜场 负场 积分
上海 22 18 4 40
北京 22 14 8 36
浙江 22 7 15 29
江西 22 0 22 22
(1)列式表示积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗
积分问题
解:观察积分榜,从最下面一行可看出,负一场积1分.
设胜一场积x分根据表中其他任意一行可以列方程,求出x的值.例如,根据第一行可列方程:
18x+1×4=40.
由此得出 x=2.
用表中其他行可以验证,得出结论:负一场积1分,胜一场积2分.
(1)如果一个队胜m场,则负(22-m)场,胜场积分为2m,负场积分为22-m,总积分为
2m+(22-m)=m+22.
三、知识讲解
(2)设一个队胜了x场,则负了(22-x)场,如果这个队的胜场总积分等于负场总积分,则有方程
其中,x (胜场)的值必须是整数,所以 不符合实际意义. 由此可以判定没有哪个队伍的胜场总积分等于负场总积分.
考试竞赛得分问题
学校组织知识竞赛,共设20道选择题,各题分值相同,每题必答,下表记录的是5名参赛者的得分情况:
参赛者 A B C D
答对数 20 19 18 14
答错数 0 1 2 6
得分 100 94 88 64
E
10
10
40
(1)由表格知,答对一题得____分,答错一题得____分。
(2)参赛者F得82分,他答对了几道题
(3)参赛者G说他得90分,你认为可能吗?为什么?
5
-1
解:(2)设他答对了x道题,则答错了 (20-x)道题。
根据题意,得 2x+(20-x)=82.
解得 x=17.
答:他答对了17道题.
(3)不可能.理由:设参赛者G答对了m道题,则答错 (20-m)道题.
根据题意,得5m+(20-m)=90.解得m=
因为m为整数,所以不符合题意,故参赛者G不可能90分.
比赛积分问题:积分问题中常用比赛总场数及比赛总得分来找相等关系。
比赛总场数=胜场数+负场数
比赛总积分=胜场积分+负场积分+平场总分
考试竞赛问题:与比赛积分问题类似,其基本的相等关系为:
总题数=答对题数+答错题数+未答题数
总得分=答对得分+答错得分+未答得分
课堂小结
实际问题
实际问题的答案
一元一次方程
一元一次方程的解(x=a)
设未知数
列方程
解方程
检验
小结
这一过程一般包括以下几个步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并答话.
小结
