2022—2023学年人教版数学八年级上册11.1.1三角形的边 课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.1.1三角形的边 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 17:33:54 | ||
图片预览



文档简介
(共17张PPT)
11.1.1 三角形的边
埃及金字塔
悉尼歌剧院
水分子结构示意图
飞机机翼
讲授新课
三角形的概念
一
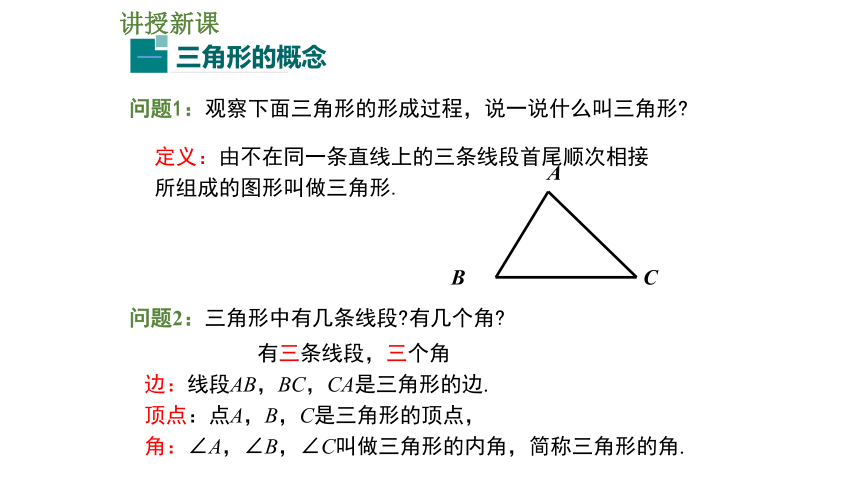
问题1:观察下面三角形的形成过程,说一说什么叫三角形
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
问题2:三角形中有几条线段 有几个角
A
B
C
有三条线段,三个角
边:线段AB,BC,CA是三角形的边.
顶点:点A,B,C是三角形的顶点,
角:∠A,∠B,∠C叫做三角形的内角,简称三角形的角.
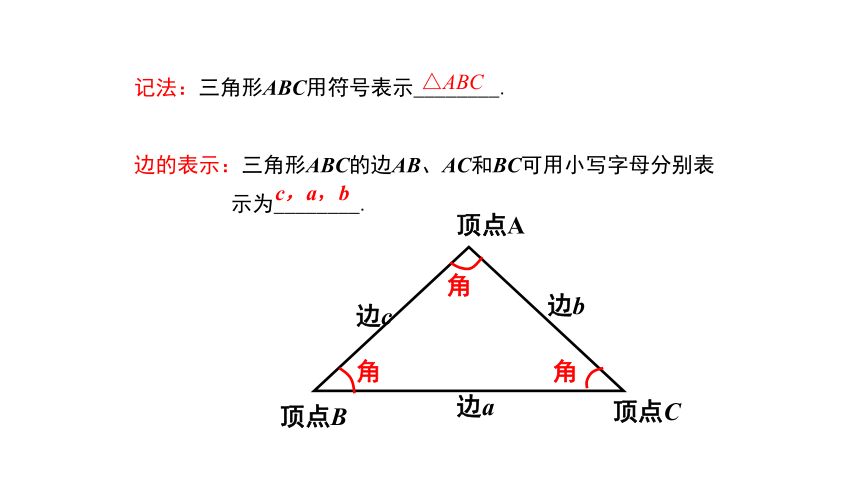
记法:三角形ABC用符号表示________.
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表
示为________.
△ABC
c,a,b
边c
边b
边a
顶点C
角
角
角
顶点A
顶点B
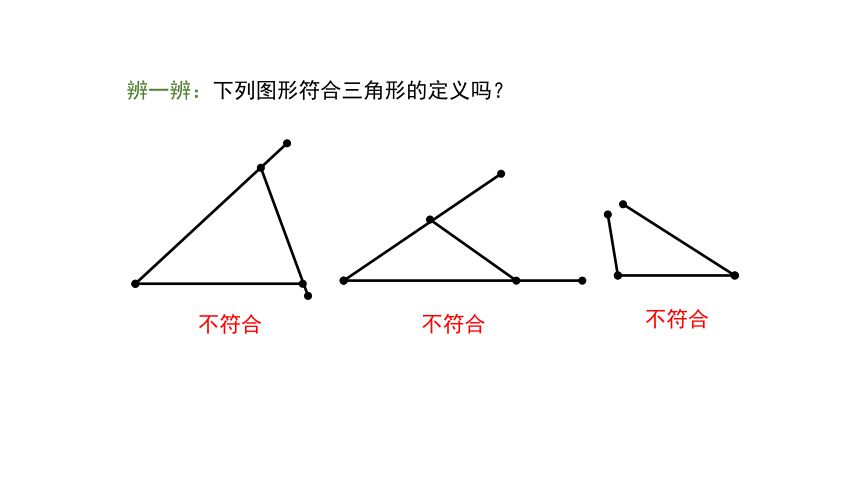
辨一辨:下列图形符合三角形的定义吗?
不符合
不符合
不符合
什么样的图形叫三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
A
B
C
顶点:用一个大写字母表示如A、B、C
边:边AB,边BC,边AC
角(内角):∠A,∠B,∠C
表示方法:记作△ABC
A
B
C
三角形的相关概念:
a
c
b
A
B
A
C
B
A
观察
三角形按角
可分为:
直角三角形
锐角三角形
钝角三角形
三角形按边
可分为:
三边都不相等
的三角形
腰与底边不相等
的等腰三角形
腰与底边相等
的等腰三角形
再观察
等腰三角形
三角形的分类
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
三角形的分类
等腰三角形
腰≠底的三角形
等边三角形
不等边三角形
等腰三角形
等边三角形
思考:三角形的三边有没有什么特殊的关系呢?
B
A
C
观察图形,回答问题。
A
B
C
判断
AB+AC BC
BC+AB AC
BC+AC AB
两点之间,
线段最短
三角形的任意两边
之和大于第三边
>
>
>
例、判断下列长度的三条线段能否拼成三角形?
(1)3cm、8cm、4cm; (2)2cm、6cm、5cm;
(3)5cm、6cm、10cm;(4)3cm、5cm、8cm;
否
能
能
否
小窍门:用较短的两条线段之和与最长的线段比较,若大,能组成三角形,反之,则不能。
自主画图,思考归纳
学生活动:在一个三角形中,任何两边之差与第三边有什么关系?画一个三角形,量出三边长度,探究上述问题,得出结论。
归纳:(1)三角形三边关系:两边之和大于第三边及两边之差小于第三边.
(2)在做题时,不仅要考虑到两边之和大于第三边,还要考虑到两边之差小于第三边。
夯实基础
例、 若三角形的两边长分别是2和7,求第三边长的范围;当第三边长为奇数,求第三边的长。
归纳:设x为三角形第三条边的长,则有两边之差解:设第三边长为x,则应有
即5x>7-2
x<7+2
因为第三边长为奇数,所以第三边长取7
巩固练习
1.等腰三角形是等边三角形。( )
2.等边三角形是特殊的等腰三角形。( )
3.三角形按边分分为等腰三角形、等边三角形、
不等边三角形。( )
4.已知等腰三角形的周长为16,且底边长为3,
则腰长是_____。
√
×
×
6.5
忆一忆今天我们学了哪些内容?
1.三角形的相关概念(边、角、顶点);
2.三角形的分类;
3.通过实践了解三角形三边之间的关系。
小结
11.1.1 三角形的边
埃及金字塔
悉尼歌剧院
水分子结构示意图
飞机机翼
讲授新课
三角形的概念
一
问题1:观察下面三角形的形成过程,说一说什么叫三角形
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
问题2:三角形中有几条线段 有几个角
A
B
C
有三条线段,三个角
边:线段AB,BC,CA是三角形的边.
顶点:点A,B,C是三角形的顶点,
角:∠A,∠B,∠C叫做三角形的内角,简称三角形的角.
记法:三角形ABC用符号表示________.
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表
示为________.
△ABC
c,a,b
边c
边b
边a
顶点C
角
角
角
顶点A
顶点B
辨一辨:下列图形符合三角形的定义吗?
不符合
不符合
不符合
什么样的图形叫三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
A
B
C
顶点:用一个大写字母表示如A、B、C
边:边AB,边BC,边AC
角(内角):∠A,∠B,∠C
表示方法:记作△ABC
A
B
C
三角形的相关概念:
a
c
b
A
B
A
C
B
A
观察
三角形按角
可分为:
直角三角形
锐角三角形
钝角三角形
三角形按边
可分为:
三边都不相等
的三角形
腰与底边不相等
的等腰三角形
腰与底边相等
的等腰三角形
再观察
等腰三角形
三角形的分类
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
三角形的分类
等腰三角形
腰≠底的三角形
等边三角形
不等边三角形
等腰三角形
等边三角形
思考:三角形的三边有没有什么特殊的关系呢?
B
A
C
观察图形,回答问题。
A
B
C
判断
AB+AC BC
BC+AB AC
BC+AC AB
两点之间,
线段最短
三角形的任意两边
之和大于第三边
>
>
>
例、判断下列长度的三条线段能否拼成三角形?
(1)3cm、8cm、4cm; (2)2cm、6cm、5cm;
(3)5cm、6cm、10cm;(4)3cm、5cm、8cm;
否
能
能
否
小窍门:用较短的两条线段之和与最长的线段比较,若大,能组成三角形,反之,则不能。
自主画图,思考归纳
学生活动:在一个三角形中,任何两边之差与第三边有什么关系?画一个三角形,量出三边长度,探究上述问题,得出结论。
归纳:(1)三角形三边关系:两边之和大于第三边及两边之差小于第三边.
(2)在做题时,不仅要考虑到两边之和大于第三边,还要考虑到两边之差小于第三边。
夯实基础
例、 若三角形的两边长分别是2和7,求第三边长的范围;当第三边长为奇数,求第三边的长。
归纳:设x为三角形第三条边的长,则有两边之差
即5
x<7+2
因为第三边长为奇数,所以第三边长取7
巩固练习
1.等腰三角形是等边三角形。( )
2.等边三角形是特殊的等腰三角形。( )
3.三角形按边分分为等腰三角形、等边三角形、
不等边三角形。( )
4.已知等腰三角形的周长为16,且底边长为3,
则腰长是_____。
√
×
×
6.5
忆一忆今天我们学了哪些内容?
1.三角形的相关概念(边、角、顶点);
2.三角形的分类;
3.通过实践了解三角形三边之间的关系。
小结
