2022—2023学年人教版数学八年级上册11.2.2三角形的外角 课件 (共15张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.2.2三角形的外角 课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 17:38:33 | ||
图片预览

文档简介
(共15张PPT)
11.2.2三角形的外角
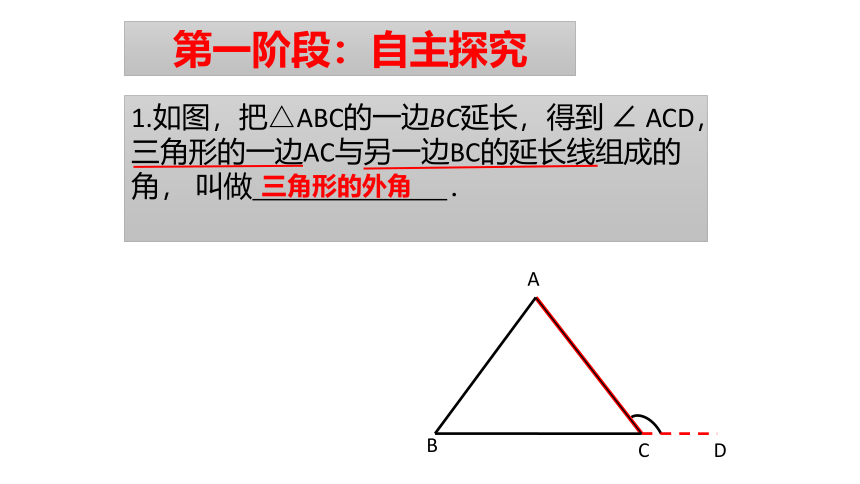
1.如图,把△ABC的一边BC延长,得到 ∠ ACD,三角形的一边AC与另一边BC的延长线组成的角, 叫做 .
三角形的外角
第一阶段:自主探究
B
A
C
D
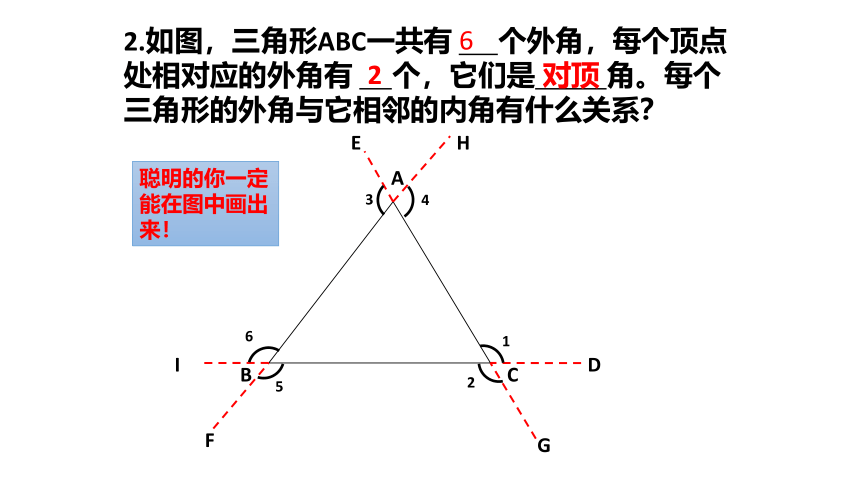
2.如图,三角形ABC一共有 个外角,每个顶点处相对应的外角有 个,它们是 角。每个三角形的外角与它相邻的内角有什么关系?
6
2
A
B
C
1
3
5
2
4
6
D
E
F
G
H
I
聪明的你一定能在图中画出来!
对顶
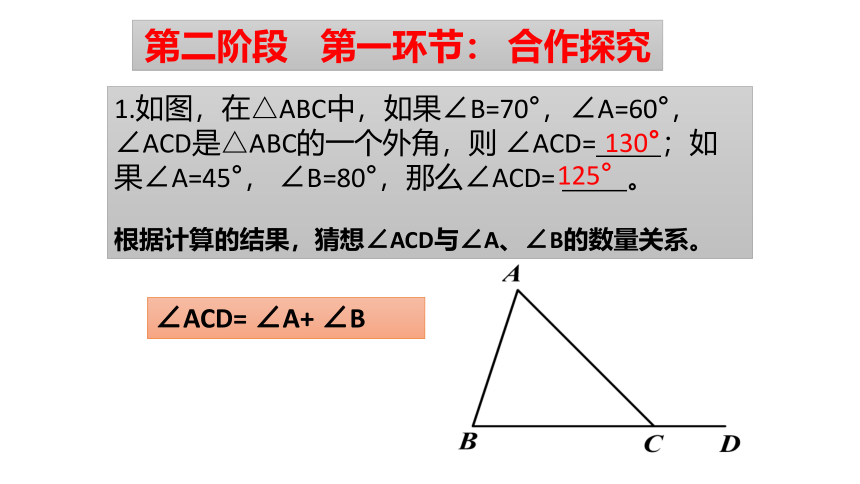
1.如图,在△ABC中,如果∠B=70°,∠A=60°,∠ACD是△ABC的一个外角,则 ∠ACD= ;如果∠A=45°, ∠B=80°,那么∠ACD= 。
根据计算的结果,猜想∠ACD与∠A、∠B的数量关系。
130°
第二阶段 第一环节: 合作探究
125°
∠ACD= ∠A+ ∠B
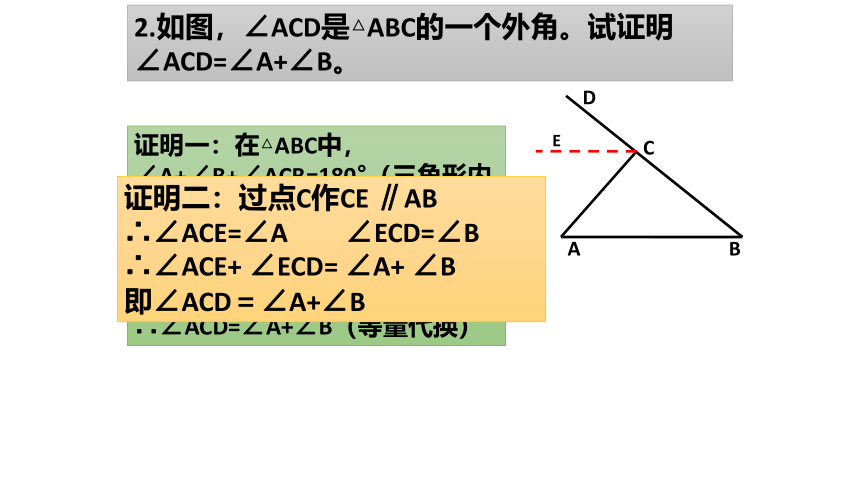
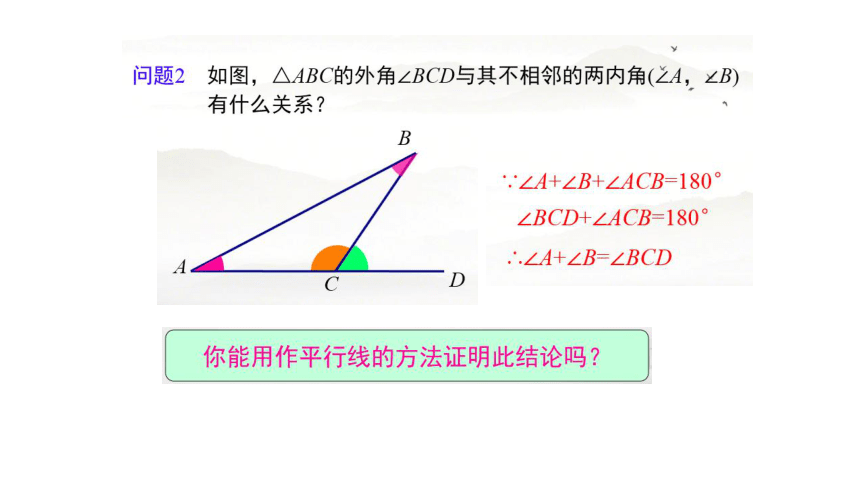
2.如图,∠ACD是△ABC的一个外角。试证明
∠ACD=∠A+∠B。
A
B
C
D
证明一:在△ABC中,
∠A+∠B+∠ACB=180°(三角形内角和定理)
∴∠ACB=180°—(∠A+∠B)
又∵∠ACB=180°—∠ACD(邻补角的定义)
∴∠ACD=∠A+∠B(等量代换)
证明二:过点C作CE ∥AB
∴∠ACE=∠A ∠ECD=∠B
∴∠ACE+ ∠ECD= ∠A+ ∠B
即∠ACD=∠A+∠B
E
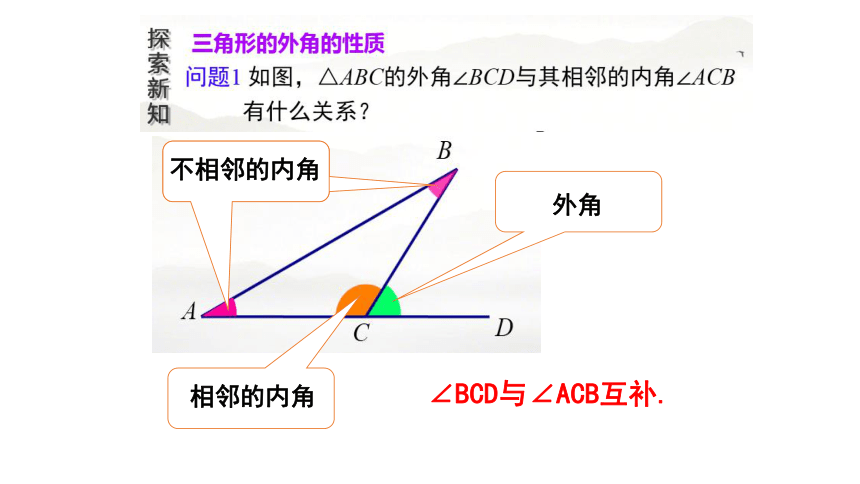
相邻的内角
外角
不相邻的内角
∠BCD与∠ACB互补.
E
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
根据平行线的性质求出∠C,
再根据三角形外角性
质即可求出∠3.
∵AB∥CD,∠1=45°,∴∠C=∠1=45°.
又∵∠2=35°,
∴∠3=∠2+∠C=35°+45°=80°.
如图,直线AB,CD被BC
所截,若AB∥CD,∠1=45°,∠2=35°,
则∠3=________度.
例1
80
图中∠1的大小等于( )
A.40°
B.50°
C.60°
D.70°
练习1
D
练习2:
如图,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A
C.∠A>∠2>∠1 D.∠2>∠A>∠1
B
如图, ∠ BAE, ∠ CBF, ∠ ACD 是△ABC的三个外角,它们的和是多少?
由三角形的一个外角等于与它不相邻的
两个内角的和,得
∠ BAE= ∠ 2+ ∠ 3,
∠ cbf= ∠ 1+ ∠ 3,
∠ ACD= ∠ 1+ ∠ 2.
所以∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3).
说出下列图形中∠ 1和∠ 2的度数:
由∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD=2×180°=360°.
例
解:
你还有其他解法吗?
1、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是3600
归纳:
11.2.2三角形的外角
1.如图,把△ABC的一边BC延长,得到 ∠ ACD,三角形的一边AC与另一边BC的延长线组成的角, 叫做 .
三角形的外角
第一阶段:自主探究
B
A
C
D
2.如图,三角形ABC一共有 个外角,每个顶点处相对应的外角有 个,它们是 角。每个三角形的外角与它相邻的内角有什么关系?
6
2
A
B
C
1
3
5
2
4
6
D
E
F
G
H
I
聪明的你一定能在图中画出来!
对顶
1.如图,在△ABC中,如果∠B=70°,∠A=60°,∠ACD是△ABC的一个外角,则 ∠ACD= ;如果∠A=45°, ∠B=80°,那么∠ACD= 。
根据计算的结果,猜想∠ACD与∠A、∠B的数量关系。
130°
第二阶段 第一环节: 合作探究
125°
∠ACD= ∠A+ ∠B
2.如图,∠ACD是△ABC的一个外角。试证明
∠ACD=∠A+∠B。
A
B
C
D
证明一:在△ABC中,
∠A+∠B+∠ACB=180°(三角形内角和定理)
∴∠ACB=180°—(∠A+∠B)
又∵∠ACB=180°—∠ACD(邻补角的定义)
∴∠ACD=∠A+∠B(等量代换)
证明二:过点C作CE ∥AB
∴∠ACE=∠A ∠ECD=∠B
∴∠ACE+ ∠ECD= ∠A+ ∠B
即∠ACD=∠A+∠B
E
相邻的内角
外角
不相邻的内角
∠BCD与∠ACB互补.
E
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
根据平行线的性质求出∠C,
再根据三角形外角性
质即可求出∠3.
∵AB∥CD,∠1=45°,∴∠C=∠1=45°.
又∵∠2=35°,
∴∠3=∠2+∠C=35°+45°=80°.
如图,直线AB,CD被BC
所截,若AB∥CD,∠1=45°,∠2=35°,
则∠3=________度.
例1
80
图中∠1的大小等于( )
A.40°
B.50°
C.60°
D.70°
练习1
D
练习2:
如图,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A
C.∠A>∠2>∠1 D.∠2>∠A>∠1
B
如图, ∠ BAE, ∠ CBF, ∠ ACD 是△ABC的三个外角,它们的和是多少?
由三角形的一个外角等于与它不相邻的
两个内角的和,得
∠ BAE= ∠ 2+ ∠ 3,
∠ cbf= ∠ 1+ ∠ 3,
∠ ACD= ∠ 1+ ∠ 2.
所以∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3).
说出下列图形中∠ 1和∠ 2的度数:
由∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD=2×180°=360°.
例
解:
你还有其他解法吗?
1、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是3600
归纳:
