人教版数学八年级上册13.1.2.1线段的垂直平分线的性质与判定 练习 (Word版含答案)
文档属性
| 名称 | 人教版数学八年级上册13.1.2.1线段的垂直平分线的性质与判定 练习 (Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 173.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 17:23:44 | ||
图片预览


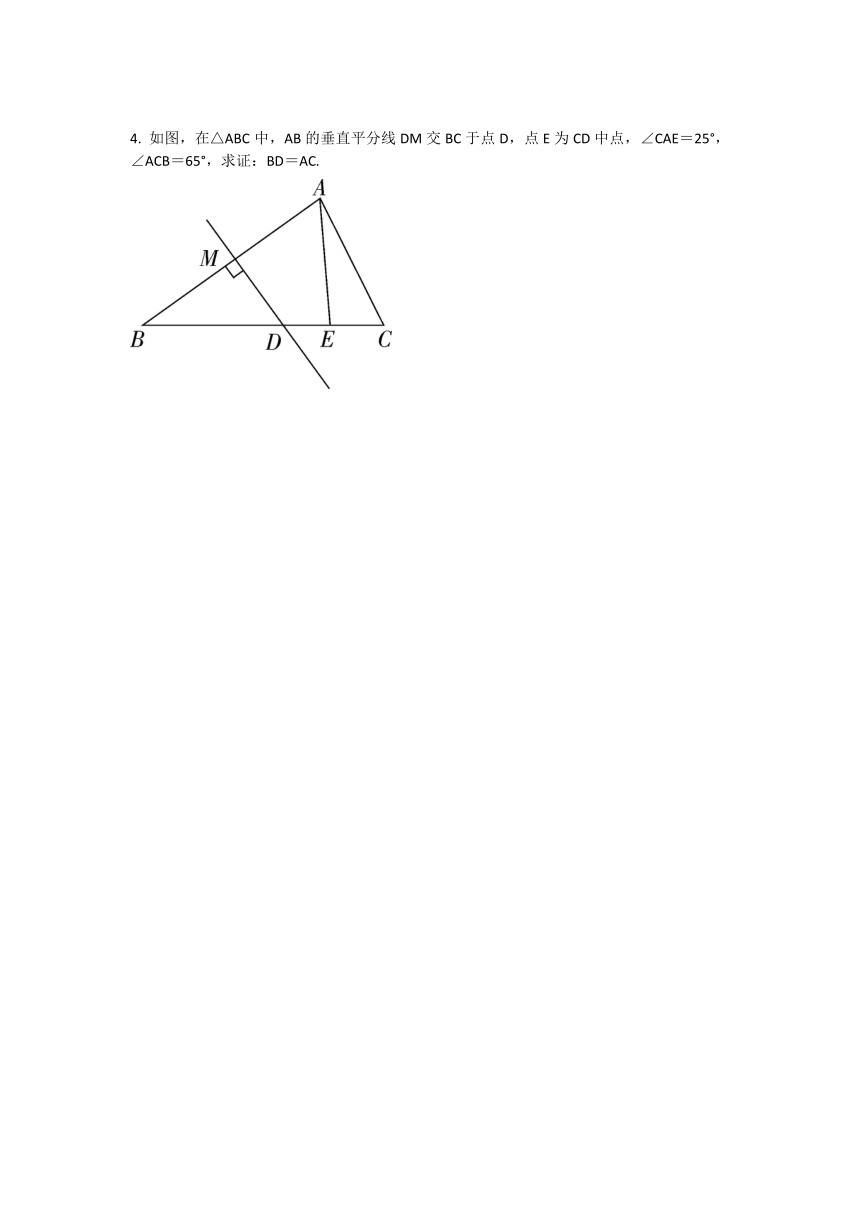
文档简介
13.1.2.1线段的垂直平分线的性质与判定
选择题
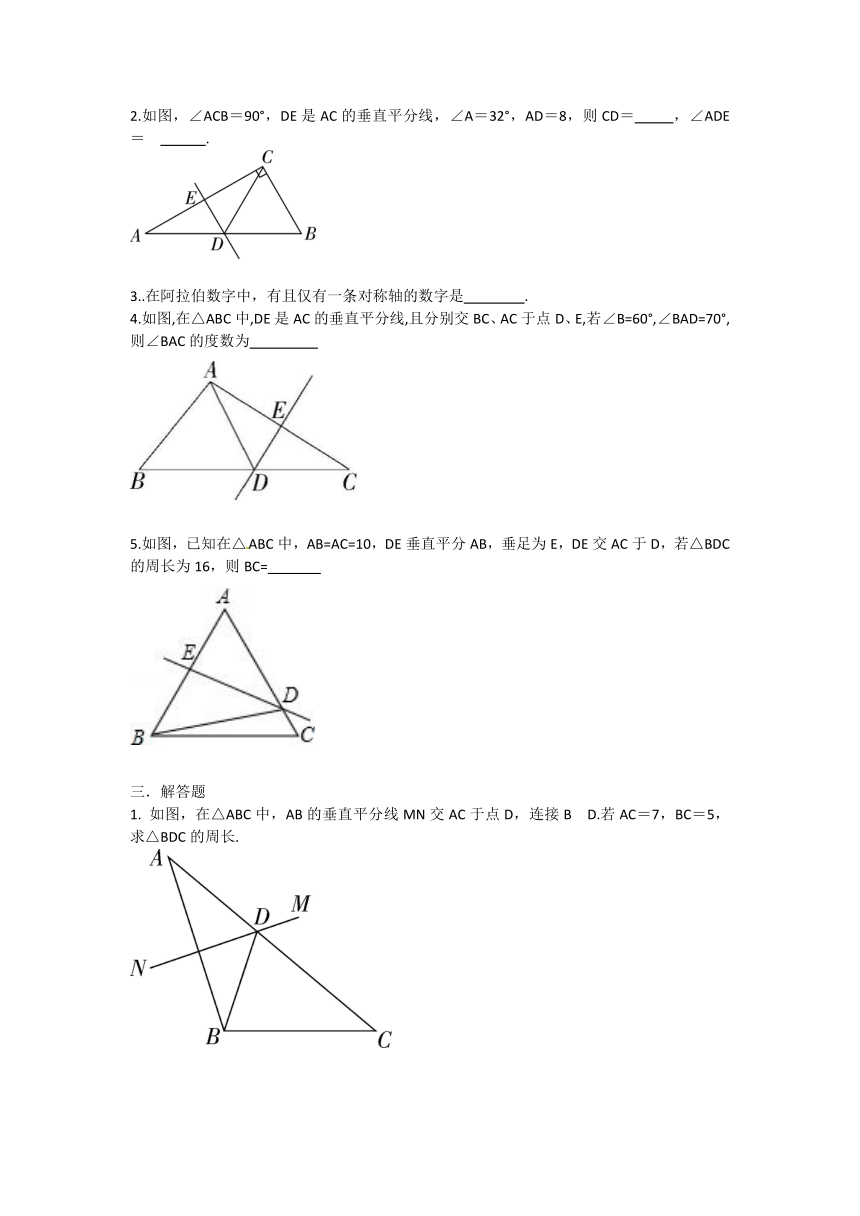
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=4,则线段PB的长度为( )
A.6 B.5 C.4 D.3
3.如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC=14 cm,BE=8 cm,则EC的长为( )
A.8 cm
B.6 cm
C.4 cm
D.2 cm
4.如图,AB是CD的垂直平分线,若AC=2.6cm,BD=1.3 cm,则四边形ACBD的周长是( )
A. 3.9 cm
B. 7.8 cm
C. 4 cm
D. 4.6 cm
5.如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于( )
A.1.5 B.2 C.2.5 D.3
6.如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )
A.10.5 B.12 C.15 D.18
填空题
1.小明做了一个如图所示的风筝,其中EH=FH,ED=FD,小明说不用测量就知道DH是EF的垂直平分线,其中蕴含的道理是 .
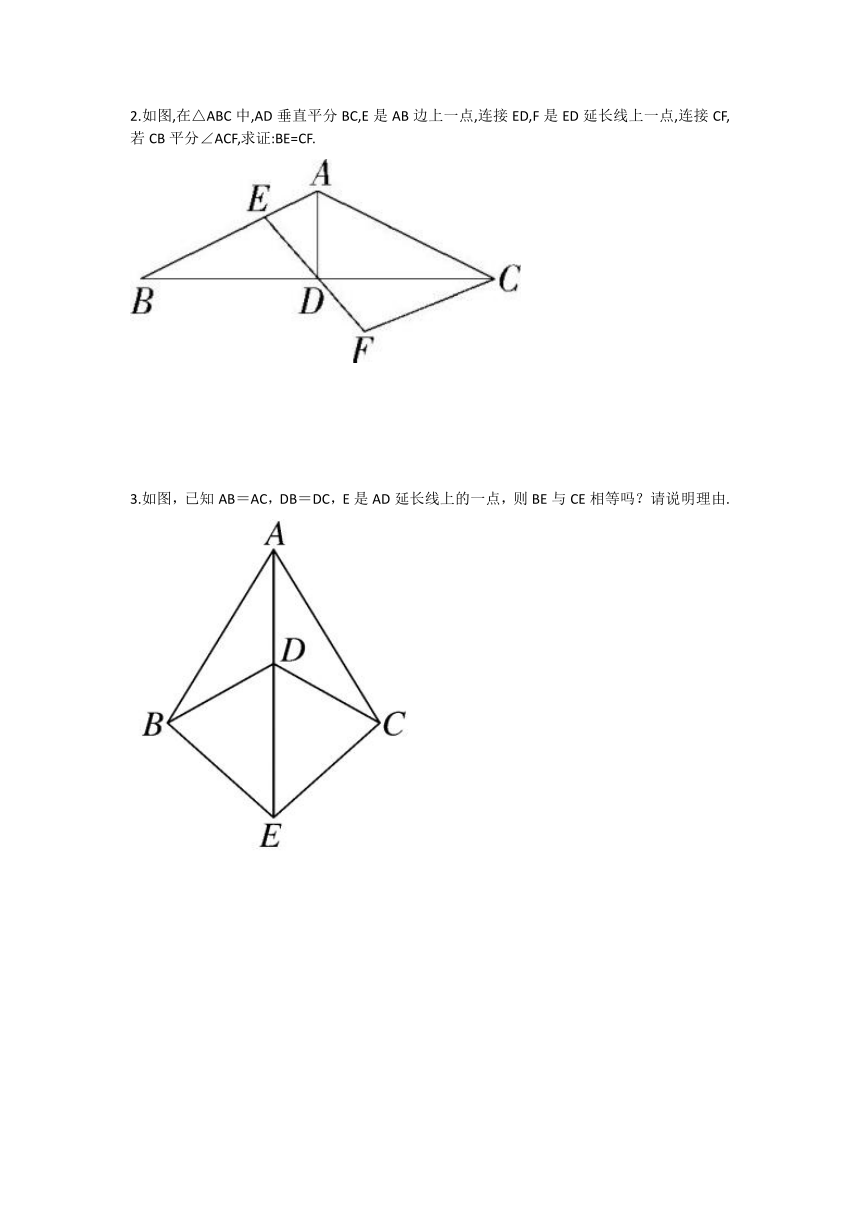
2.如图,∠ACB=90°,DE是AC的垂直平分线,∠A=32°,AD=8,则CD= ,∠ADE= .
3..在阿拉伯数字中,有且仅有一条对称轴的数字是 .
4.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D、E,若∠B=60°,∠BAD=70°,则∠BAC的度数为
5.如图,已知在△ABC中,AB=AC=10,DE垂直平分AB,垂足为E,DE交AC于D,若△BDC的周长为16,则BC=
解答题
1. 如图,在△ABC中,AB的垂直平分线MN交AC于点D,连接B D.若AC=7,BC=5,求△BDC的周长.
2.如图,在△ABC中,AD垂直平分BC,E是AB边上一点,连接ED,F是ED延长线上一点,连接CF,若CB平分∠ACF,求证:BE=CF.
3.如图,已知AB=AC,DB=DC,E是AD延长线上的一点,则BE与CE相等吗?请说明理由.
4. 如图,在△ABC中,AB的垂直平分线DM交BC于点D,点E为CD中点,∠CAE=25°,∠ACB=65°,求证:BD=AC.
13.1.2.1线段的垂直平分线的性质与判定
参考答案
一.选择题
1.如图,AC=AD,BC=BD,则有( A )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=4,则线段PB的长度为( C)
A.6 B.5 C.4 D.3
3.如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC=14 cm,BE=8 cm,则EC的长为( B )
A.8 cm
B.6 cm
C.4 cm
D.2 cm
4.如图,AB是CD的垂直平分线,若AC=2.6cm,BD=1.3 cm,则四边形ACBD的周长是( B )
A. 3.9 cm
B. 7.8 cm
C. 4 cm
D. 4.6 cm
5.如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于( B )
A.1.5 B.2 C.2.5 D.3
6.如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( C )
A.10.5 B.12 C.15 D.18
二.填空题
1.小明做了一个如图所示的风筝,其中EH=FH,ED=FD,小明说不用测量就知道DH是EF的垂直平分线,其中蕴含的道理是 与线段两个端点距离相等的点在这条线段的垂直平分线上 .
2.如图,∠ACB=90°,DE是AC的垂直平分线,∠A=32°,AD=8,则CD= 8 ,∠ADE= 58° .
3..在阿拉伯数字中,有且仅有一条对称轴的数字是 3 .
4.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D、E,若∠B=60°,∠BAD=70°,则∠BAC的度数为 95°
5.如图,已知在△ABC中,AB=AC=10,DE垂直平分AB,垂足为E,DE交AC于D,若△BDC的周长为16,则BC= 6
三.解答题
1. 如图,在△ABC中,AB的垂直平分线MN交AC于点D,连接B D.若AC=7,BC=5,求△BDC的周长.
解:∵NM是AB的垂直平分线,∴DA=DB.
∴BD+CD+BC=AD+CD+BC=AC+BC=12,
即△BDC的周长为12.
2.如图,在△ABC中,AD垂直平分BC,E是AB边上一点,连接ED,F是ED延长线上一点,连接CF,若CB平分∠ACF,求证:BE=CF.
证明 ∵AD垂直平分BC,∴AB=AC,BD=DC,
在Rt△ABD和Rt△ACD中,
∴Rt△ABD≌Rt△ACD(HL),∴∠ABC=∠ACB,
∵CB平分∠ACF,∴∠FCB=∠ACB,∴∠ABC=∠FCB,
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA),∴BE=CF.
3.如图,已知AB=AC,DB=DC,E是AD延长线上的一点,则BE与CE相等吗?请说明理由.
解:BE=CE.理由如下:
如图,连接BC.
∵AB=AC,
∴点A在线段BC的垂直平分线上.
同理,点D也在线段BC的垂直平分线上.
∵两点确定一条直线,
∴AD是线段BC的垂直平分线.
∵E是AD延长线上的一点,
∴BE=CE.
4. 如图,在△ABC中,AB的垂直平分线DM交BC于点D,点E为CD中点,∠CAE=25°,∠ACB=65°,求证:BD=AC.
证明:连接AD,
∵∠CAE=25°,∠ACB=65°,
∴∠AED=∠CAE+∠ACB=90°,即AE⊥DC.
∵点E为CD中点,
∴DE=CE.
在△ADE和△ACE中,
∴△ADE≌△ACE(SAS).
∴AD=AC.
∵AB的垂直平分线DM交BC于点D,
∴BD=AD.∴BD=AC.
选择题
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=4,则线段PB的长度为( )
A.6 B.5 C.4 D.3
3.如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC=14 cm,BE=8 cm,则EC的长为( )
A.8 cm
B.6 cm
C.4 cm
D.2 cm
4.如图,AB是CD的垂直平分线,若AC=2.6cm,BD=1.3 cm,则四边形ACBD的周长是( )
A. 3.9 cm
B. 7.8 cm
C. 4 cm
D. 4.6 cm
5.如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于( )
A.1.5 B.2 C.2.5 D.3
6.如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )
A.10.5 B.12 C.15 D.18
填空题
1.小明做了一个如图所示的风筝,其中EH=FH,ED=FD,小明说不用测量就知道DH是EF的垂直平分线,其中蕴含的道理是 .
2.如图,∠ACB=90°,DE是AC的垂直平分线,∠A=32°,AD=8,则CD= ,∠ADE= .
3..在阿拉伯数字中,有且仅有一条对称轴的数字是 .
4.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D、E,若∠B=60°,∠BAD=70°,则∠BAC的度数为
5.如图,已知在△ABC中,AB=AC=10,DE垂直平分AB,垂足为E,DE交AC于D,若△BDC的周长为16,则BC=
解答题
1. 如图,在△ABC中,AB的垂直平分线MN交AC于点D,连接B D.若AC=7,BC=5,求△BDC的周长.
2.如图,在△ABC中,AD垂直平分BC,E是AB边上一点,连接ED,F是ED延长线上一点,连接CF,若CB平分∠ACF,求证:BE=CF.
3.如图,已知AB=AC,DB=DC,E是AD延长线上的一点,则BE与CE相等吗?请说明理由.
4. 如图,在△ABC中,AB的垂直平分线DM交BC于点D,点E为CD中点,∠CAE=25°,∠ACB=65°,求证:BD=AC.
13.1.2.1线段的垂直平分线的性质与判定
参考答案
一.选择题
1.如图,AC=AD,BC=BD,则有( A )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=4,则线段PB的长度为( C)
A.6 B.5 C.4 D.3
3.如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC=14 cm,BE=8 cm,则EC的长为( B )
A.8 cm
B.6 cm
C.4 cm
D.2 cm
4.如图,AB是CD的垂直平分线,若AC=2.6cm,BD=1.3 cm,则四边形ACBD的周长是( B )
A. 3.9 cm
B. 7.8 cm
C. 4 cm
D. 4.6 cm
5.如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于( B )
A.1.5 B.2 C.2.5 D.3
6.如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( C )
A.10.5 B.12 C.15 D.18
二.填空题
1.小明做了一个如图所示的风筝,其中EH=FH,ED=FD,小明说不用测量就知道DH是EF的垂直平分线,其中蕴含的道理是 与线段两个端点距离相等的点在这条线段的垂直平分线上 .
2.如图,∠ACB=90°,DE是AC的垂直平分线,∠A=32°,AD=8,则CD= 8 ,∠ADE= 58° .
3..在阿拉伯数字中,有且仅有一条对称轴的数字是 3 .
4.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D、E,若∠B=60°,∠BAD=70°,则∠BAC的度数为 95°
5.如图,已知在△ABC中,AB=AC=10,DE垂直平分AB,垂足为E,DE交AC于D,若△BDC的周长为16,则BC= 6
三.解答题
1. 如图,在△ABC中,AB的垂直平分线MN交AC于点D,连接B D.若AC=7,BC=5,求△BDC的周长.
解:∵NM是AB的垂直平分线,∴DA=DB.
∴BD+CD+BC=AD+CD+BC=AC+BC=12,
即△BDC的周长为12.
2.如图,在△ABC中,AD垂直平分BC,E是AB边上一点,连接ED,F是ED延长线上一点,连接CF,若CB平分∠ACF,求证:BE=CF.
证明 ∵AD垂直平分BC,∴AB=AC,BD=DC,
在Rt△ABD和Rt△ACD中,
∴Rt△ABD≌Rt△ACD(HL),∴∠ABC=∠ACB,
∵CB平分∠ACF,∴∠FCB=∠ACB,∴∠ABC=∠FCB,
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA),∴BE=CF.
3.如图,已知AB=AC,DB=DC,E是AD延长线上的一点,则BE与CE相等吗?请说明理由.
解:BE=CE.理由如下:
如图,连接BC.
∵AB=AC,
∴点A在线段BC的垂直平分线上.
同理,点D也在线段BC的垂直平分线上.
∵两点确定一条直线,
∴AD是线段BC的垂直平分线.
∵E是AD延长线上的一点,
∴BE=CE.
4. 如图,在△ABC中,AB的垂直平分线DM交BC于点D,点E为CD中点,∠CAE=25°,∠ACB=65°,求证:BD=AC.
证明:连接AD,
∵∠CAE=25°,∠ACB=65°,
∴∠AED=∠CAE+∠ACB=90°,即AE⊥DC.
∵点E为CD中点,
∴DE=CE.
在△ADE和△ACE中,
∴△ADE≌△ACE(SAS).
∴AD=AC.
∵AB的垂直平分线DM交BC于点D,
∴BD=AD.∴BD=AC.
