函数的概念

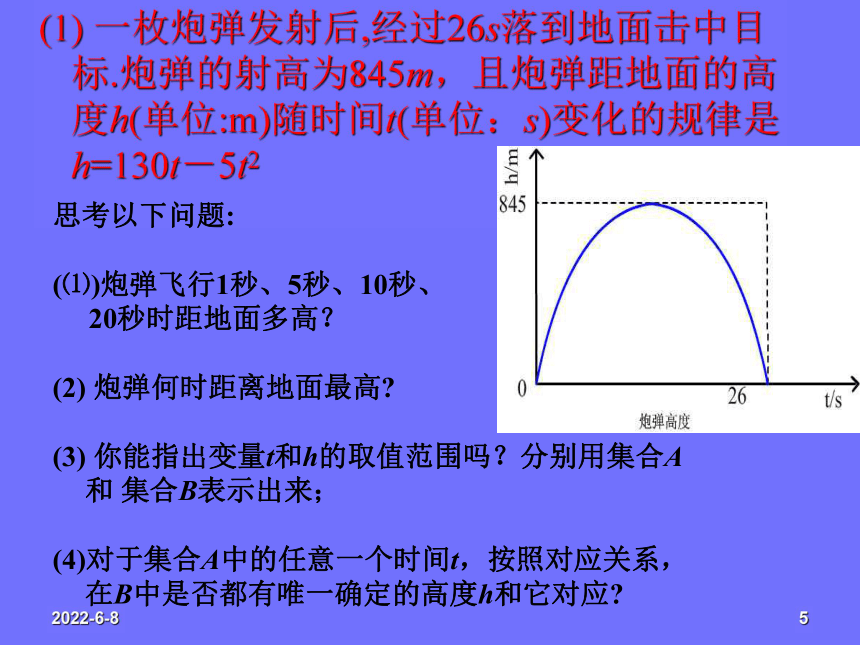
课件71张PPT。§1.2 函数及其表示 设在一个变化过程中有两个变量x与y，如果对于x的每一个值，y都有惟一的值与它对应，则称x是自变量，y是x的函数。1、初中学习的函数概念是什么？思考？一、【回忆过去】学习过程§1.2.1 函数的概念2、请问：我们在初中学过哪些函数？3、请同学们考虑以下两个问题：显然，仅用初中函数的概念很难回答这些问题。因此，需要从新的高度认识函数。2019/1/155(1) 一枚炮弹发射后,经过26s落到地面击中目 标.炮弹的射高为845m，且炮弹距地面的高度h(单位:m)随时间t(单位：s)变化的规律是 h=130t－5t2
思考以下问题:
炮弹飞行1秒、5秒、10秒、
20秒时距地面多高？
(2) 炮弹何时距离地面最高?
(3) 你能指出变量t和h的取值范围吗？分别用集合A和 集合B表示出来；
(4)对于集合A中的任意一个时间t，按照对应关系，在B中是否都有唯一确定的高度h和它对应?
环节1：实例 (1)一枚炮弹发射后，经过26s落到地面击中目标，炮弹的射高为845m，且炮弹距地面的高度h(单位：m)随时间t(单位:s)变化的规律是
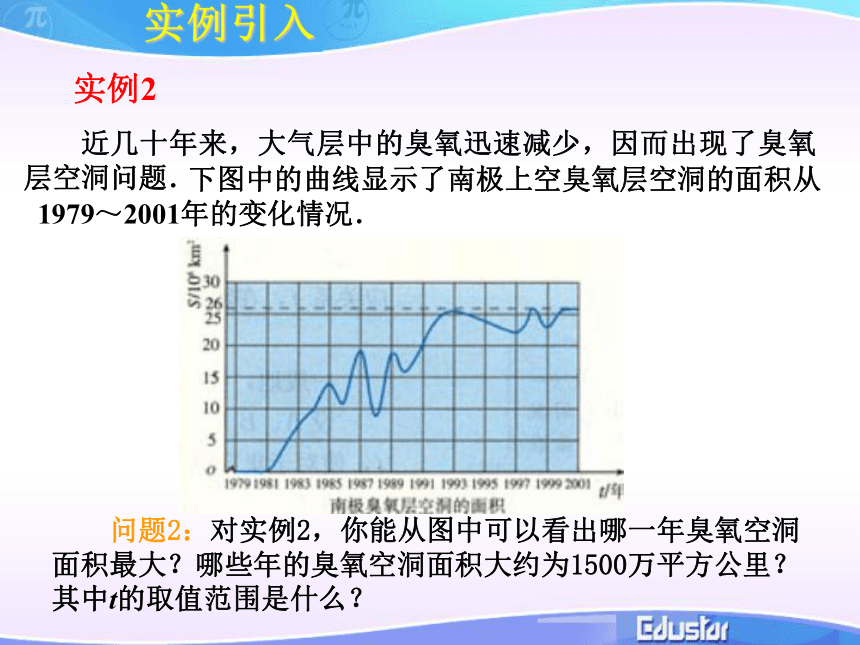
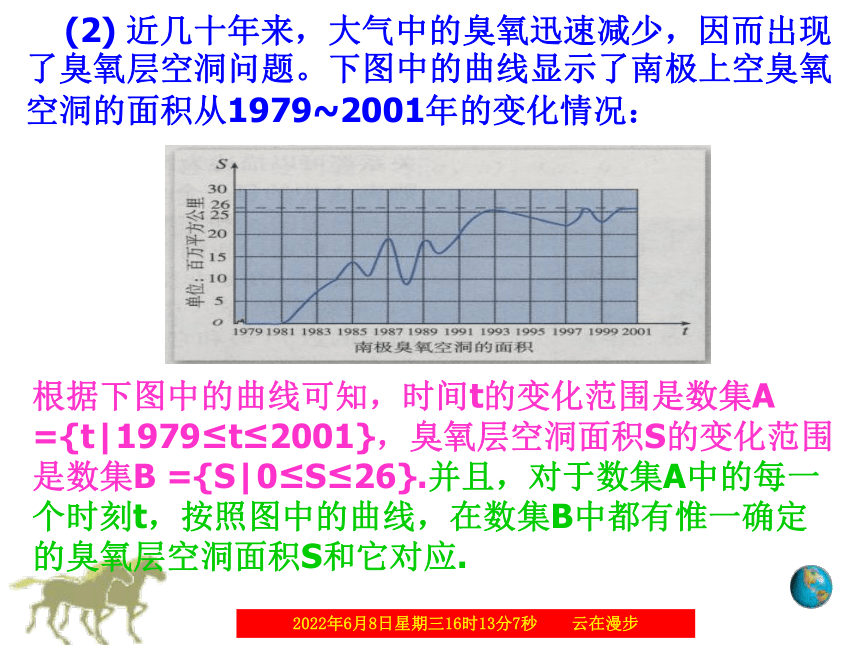
h=130t-5t2 (*)炮弹飞行时间t的变化范围是数集A={t|0≤t≤26},炮弹距地面的高度h的变化范围是数集B={h|0≤h≤845}从问题的实际意义可知，对于数集A中的任意一个时间t，按照对应关系(*)，在数集B中都有惟一的高度h和它对应。二、【新课探究】臭氧层破坏对人体健康的危害实例2 近几十年来，大气层中的臭氧迅速减少，因而出现了臭氧层空洞问题．实例引入实例2 近几十年来，大气层中的臭氧迅速减少，因而出现了臭氧层空洞问题．实例引入 下图中的曲线显示了南极上空臭氧层空洞的面积从1979～2001年的变化情况． 问题2：对实例2，你能从图中可以看出哪一年臭氧空洞面积最大？哪些年的臭氧空洞面积大约为1500万平方公里？其中t的取值范围是什么？ (2) 近几十年来，大气中的臭氧迅速减少，因而出现了臭氧层空洞问题。下图中的曲线显示了南极上空臭氧空洞的面积从1979~2001年的变化情况：根据下图中的曲线可知，时间t的变化范围是数集A ={t|1979≤t≤2001}，臭氧层空洞面积S的变化范围是数集B ={S|0≤S≤26}.并且，对于数集A中的每一个时刻t，按照图中的曲线，在数集B中都有惟一确定的臭氧层空洞面积S和它对应.2019/1/1510（3） “八五”计划以来我国城镇居民恩格尔系数变化情况请问：(1)恩格尔系数与时间之间的关系是否和前两个事例
中的两个变量之间的关系相似？(2)如何用集合与对应的语言来描述这个关系？不同点共同点实例（1）是用解析式刻画变量之间的对应关系，
实例（2）是用图象刻画变量之间的对应关系，
实例（3）是用表格刻画变量之间的对应关系；（1）都有两个非空数集
（2）两个数集之间都有一种确定的对应关系 归纳以上三个实例，我们看到，三个实例中变量之间的关系可以描述为：
对于数集A中的每一个x，按照某种对应关系f，在数集B中都有惟一确定的y和它对应，记作
f: A→B.环节2：函数的定义 函数的定义：设A、B是非空数集，如果按照某种对应关系f，使对于集合A中的任意一个数x，在集合B中都有惟一确定的数f(x)和它对应，那么就称f: A→B为从集合A到集合B的一个函数，
记作 y=f(x) , x∈A x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y的值叫做函数值，函数值的集合{f(x)|x∈A}叫做函数的值域。 {f(x)|x∈A} B　　讨论：初、高中分别对函数概念给出了定义，对这两个定义进行比较，说说引入新定义的必要性．通过比较你对函数有什么新的认识？函数概念　　你能举出生活中其他一些函数的例子吗？ 生活中的函数火箭发射时速度与时间的关系　　你能举出生活中一些函数的例子吗？ 生活中的函数我国人口出生率变化图　　你能举出生活中一些函数的例子吗？ 生活中的函数某城市一年中各月份与其平均温度的关系　　你能举出生活中一些函数的例子吗？ 生活中的函数平抛球时位移S和时间t的关系　　你能举出生活中一些函数的例子吗？ 生活中的函数两种物质的溶解度与温度的关系2019/1/1520
(1)已知集合A＝{1，2，3，4}，B＝{5，6，7}，在下列A到B的四种对应关系中，能确定A到B的函数关系的个数是(　　)
A．1　　　　
B．2
C．3
D．4B 可以一对一 或 多对一，绝不能一对多；集合A中元素不可以剩余，集合B中可以剩余。2019/1/15212．已知x∈A，y∈B，在以下的对应中，y不是x的函数的是(如下图)(　　)A对函数概念的理解
(1)如何判断给定的两个变量之间是否具有函数关系？
1、函数必须是两个非空数集间的一种对应；
2、 f：A→B表示从A到B的函数（具有方向性，同B到A不一样）它表示对于集合A中的任意一个数x，在集合B中都有唯一确定的一个数f(x)和它对应. (A无余，B可余;可以一对一、多对一，但不能一对多。）
(2)f(x)的符号含义：y=f(x)为“y是x的函数”的数学表示，仅是一个函数符号，并非表示f(x)是f与x相乘 ；符号f(a)与f(x)既有区别又有联系，f(a)表示当自变量x＝a时函数f(x)的值，而f(x)是自变量x的函数．一般情况下，f(x)是一个变量，f(a)是f(x)的一个特殊值；
(3)f 表示对应关系，也可用g、F、G……表示均可(4)函数必须具备三个要素：定义域A，值域C，对应关系f，缺一不可。注意：C?B（5）相同的函数：定义域和对应法则都相同的函数判断正误
1、函数值域中的每一个数在定义域中至少有一个数与 之对应
2、函数的定义域和值域一定是无限集合
3、定义域和对应关系确定后，函数值域也就确定
4、若函数的定义域只有一个元素，则值域也只有一 个元素
5、对于不同的x , y的值也不同
6、f (a)表示当x = a时，函数f (x)的值，是一个常量√√√√××2019/1/1525【例1】
1、选择题.给出下列从A到B的对应：
①A＝N，B＝{0,1}，对应关系是：A中的元素除以2所得的余数
②A＝{0,1,2}，B＝{4,1,0}，对应关系是f：x→y＝x2
其中表示从集合A到集合B的函数有(　　)个．
A．1　　 　B．2　　 　C．3　　 　D．0
[解析]　由于③中，0这个元素在B中无对应元素，故不是函数，因此选B.B2、判断下列对应能否表示y是x的函数（1） y=|x| （2）|y|=x
（3） y=x 2 （4）y2 =x
（5） y2+x2=1 （6）y2-x2= 1
（7）y=1 (8)x=1
(9) y= (1)能 (2)不能 (5)不能 (3)能 (4)不能 (6 )不能 3、判断下列图象能表示函数图象的是（ ）D2019/1/15284．下列各图中，不可能表示函数y＝f(x)的图象的是(　　)B2019/1/1529[答案]　B
[解析]　B图中，作垂直于x轴的直线，与图形可以有两个交点，故存在x，有两个y值与之对应，故B图y不是x的函数．2019/1/15305．A＝{x|0≤x≤2}，B＝{y|1≤y≤2}，下列图形中能表示以A为定义域，B为值域的函数的是(　　)B2019/1/1531[答案]　B
[解析]　A、C、D的值域都不是[1,2]，故选B.
2019/1/15332019/1/15342019/1/1535设a,b是两个实数，而且a(1)、满足不等式a≤x≤b的实数x的集合叫做闭区间，表示为 [a,b]
(2)、满足不等式a(1)、满足不等式a≤xa ,x ≤b, x实数集R可以用区间表示为（－∞，+∞）；
“∞”读作“无穷大”；
“－∞”读作“负无穷大”，“+∞”读作“正无穷大”.
注意：
当包括端点时，区间是中括号，不包括端点时，区间一端是小括号
2019/1/1539a（1）{x|5 ≤ x<6}
（2） {x|x ≥9}
（3） {x|x ≤ -1} ∩{x| -5 ≤ x<2}
（4） {x|x < -9}∪{x| -9 < x<20}注意：①区间是一种表示连续性的数集②定义域、值域常用区间表示或者集合表示 ③区间不能表示单元素集2019/1/1542练习 把下列集合用区间表示出来:
1、 {x|22、 {x|x≤2}
3、 {x|24、 {x|x≠0}
5 、{x|2≤x<3}
(2，3)(－ ∞，2)(2，3)或（5，9）(－∞，0)或(0，+ ∞)[2，3)环节3：回顾已学函数 初中各类函数的对应法则、定义域、值域分别是什么？RRRRR2019/1/1545探究结论实数集R 使分母不等于0的实数的集合使根号内的式子大于等于0的实数的集合R
2019/1/1546探究结论使f (x)不等于0的实数的集合使各部分式子都有意义的实数的集合(即各集合的交集)使实际问题有意义的实数的集合 0（1）求函数的定义域三、【例题演示】注意①研究一个函数一定在其定义域内研究，所以求定义域是研究任何函数的前提 ②函数的定义域常常由其实际背景决定，若只给出解析式时,定义域就是使这个式子有意义的实数x的集合.2019/1/15482019/1/1549[解析]　①要使函数有意义，只要－x2＋5x－6＞0，即－(x－2)(x－3)>0，∴2＜x＜3.
故函数的定义域为{x|2＜x＜3}．2019/1/1550[答案]　{x∈R且x≠－1，x≠－2}2019/1/15512019/1/1552 周长为l的铁丝弯成下部为矩形，上部为半圆形的框架(如右图所示)．若矩形底边长为2x，求此框架围成图形的面积y关于x的函数，并求出定义域．2019/1/1553引入： 已知f(x)=2x+3
（1）求f(2),f(3)的值
（2）求f(x+1)
（3）求f(3x-7)（三）复合函数的定义域例2分析:1、定义域就是X的取值范围
2.对应关系f对括号内的式子起作用，f不变，括号内的式子范围就不变。（三）复合函数的定义域例2解:由题意知:对于抽象函数的定义域，在同一对应关系f下，括号内整体的取值范围相同.2019/1/1557复合函数定义域的求法
A) 已知f(x)定义域为[a，b]，求f[φ(x)]定义
域，应使a≤φ(x) ≤b，解出x的范围即
可；
重难点解：由题意知:2019/1/1559复合函数定义域的求法

B)已知f[φ(x)]定义域为[a，b] ，求f(x)定义
域，即求当x∈[a，b]时，φ(x)的值域．重难点复合函数问题的拓展探究点2 函数的值域例4 求下列函数的值域.求函数的值域，应先确定定义域，树立定义域优先原则，再根据具体情况求y的取值范围．配方法观察法你能求出下列函数的值域吗？解：∴函数的值域为分离常数法换元法函数的值域用集合或区间表示求下列函数的值域：应用三：求函数值与函数的值域直接法配方法分离常数法观察法观察法换元法判别式法求函数的值域，应先确定定义域，树立定义域优先原则，再根据具体情况求y的取值范围．求下列函数的值域：四、【要点小结】3.会求简单函数的定义域和函数值4.理解区间是表示数集的一种方法，会把不等式转化为区间。2019/1/1570[例4]　某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．
(1)当每辆车的月租金定为3600元时，能租出多少辆车？
(2)当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？2019/1/1571