湘教版数学八年级上册课课练:第2章 三角形 专题 全等三角形的基本模型(含答案)
文档属性
| 名称 | 湘教版数学八年级上册课课练:第2章 三角形 专题 全等三角形的基本模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 160.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 14:27:27 | ||
图片预览

文档简介
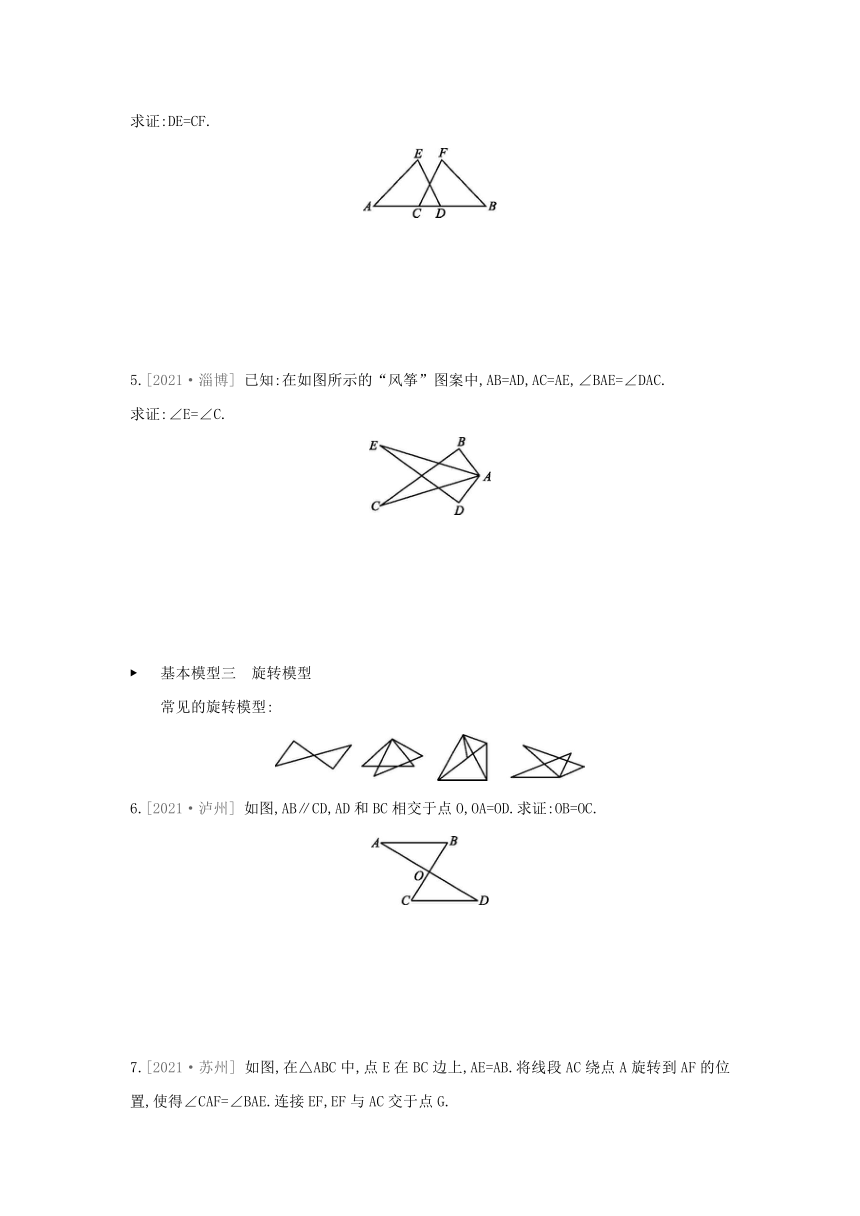
专题训练 全等三角形的基本模型
基本模型一 平移模型
常见的平移模型:
1.如图,B是线段AD的中点,BC∥DE,BC=ED.
求证:∠A=∠EBD.
2.如图,点A,B,C,D在一条直线上,AB=CD,AE∥BF,CE∥DF.
求证:AE=BF.
基本模型二 轴对称模型
常见的轴对称模型:
3.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.
求证:BE=CD.
4.如图,A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF.
求证:DE=CF.
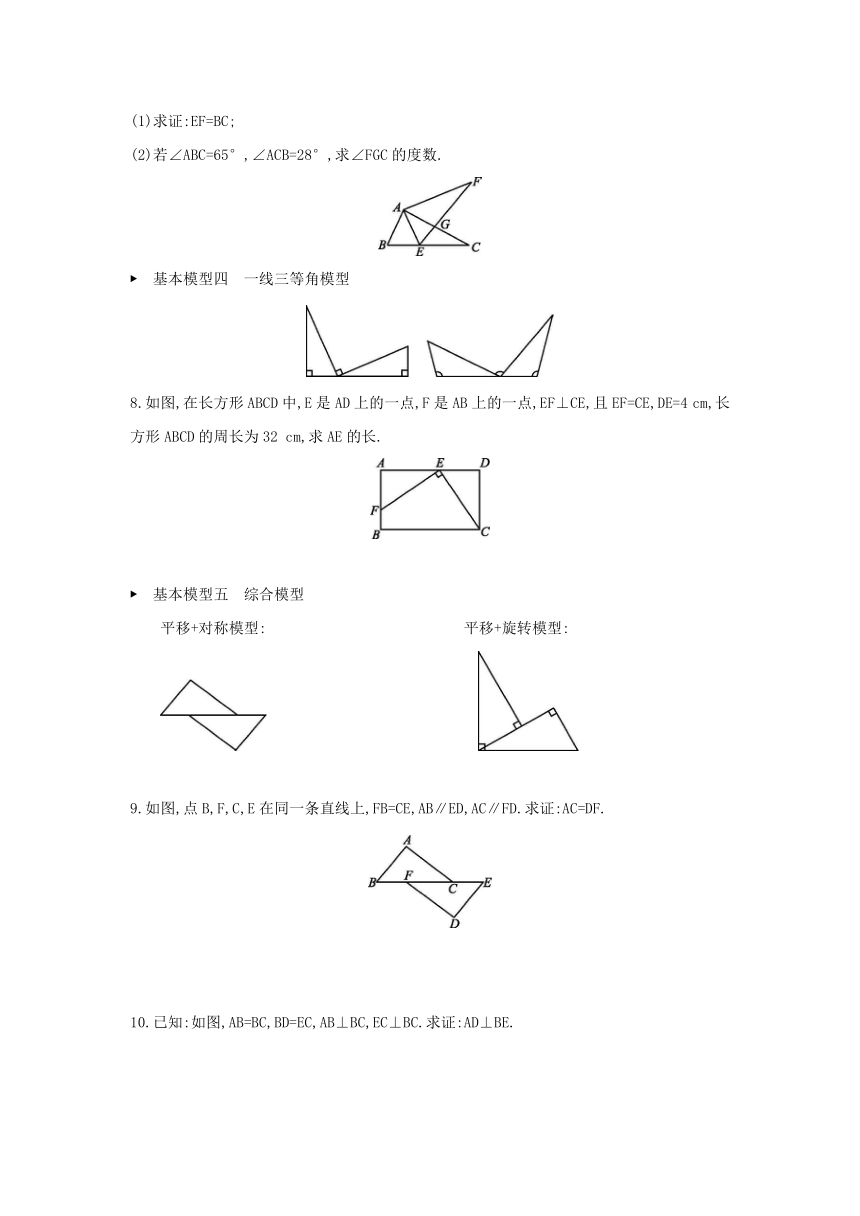
5.[2021·淄博] 已知:在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.
求证:∠E=∠C.
基本模型三 旋转模型
常见的旋转模型:
6.[2021·泸州] 如图,AB∥CD,AD和BC相交于点O,OA=OD.求证:OB=OC.
7.[2021·苏州] 如图,在△ABC中,点E在BC边上,AE=AB.将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE.连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
基本模型四 一线三等角模型
8.如图,在长方形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥CE,且EF=CE,DE=4 cm,长方形ABCD的周长为32 cm,求AE的长.
基本模型五 综合模型
平移+对称模型: 平移+旋转模型:
9.如图,点B,F,C,E在同一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AC=DF.
10.已知:如图,AB=BC,BD=EC,AB⊥BC,EC⊥BC.求证:AD⊥BE.
答案
专题训练 全等三角形的基本模型
1.证明:∵B是线段AD的中点,∴AB=BD.
∵BC∥DE,∴∠ABC=∠D.
在△ABC和△BDE中,
∴△ABC≌△BDE(SAS),∴∠A=∠EBD.
2.证明:∵AE∥BF,∴∠A=∠FBD.
∵CE∥DF,∴∠ACE=∠D.
∵AB=CD,∴AB+BC=CD+BC,即AC=BD.
在△ACE和△BDF中,
∴△ACE≌△BDF(ASA),∴AE=BF.
3.证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°.
在△ADB和△AEC中,
∴△ADB≌△AEC(ASA),∴AB=AC.
又AD=AE,∴AB-AE=AC-AD,即BE=CD.
4.证明:∵AC=BD,∴AC+CD=BD+CD,
即AD=BC.
在△AED和△BFC中,
∴△AED≌△BFC(ASA),∴DE=CF.
5.证明:∵∠BAE=∠DAC,∴∠BAE+∠EAC=∠DAC+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,,
∴△ABC≌△ADE(SAS),∴∠E=∠C.
6.证明:∵AB∥CD,∴∠A=∠D,∠B=∠C.
在△AOB和△DOC中,
∴△AOB≌△DOC(AAS),∴OB=OC.
7.解:(1)证明:∵线段AC绕点A旋转到AF的位置, ∴AC=AF.
∵∠CAF=∠BAE,
∴∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC.
在△ABC和△AEF中,
∴△ABC≌△AEF (SAS), ∴EF=BC.
(2)∵AE=AB,∴∠AEB=∠ABC= 65°.
∵ △ABC≌△AEF,
∴∠AEF=∠ABC= 65°,
∴∠FEC=180°-∠AEB-∠AEF=180°- 65°-65°= 50°.
∵∠FGC是△EGC的一个外角,∠ACB=28°,
∴ ∠FGC=∠FEC+∠ACB =50°+ 28°=78°.
8.解:∵EF⊥CE,∴∠FEC=90°,
∴∠AEF+∠DEC=90°.
又∵∠DCE+∠DEC=90°,
∴∠AEF=∠DCE.
又∵∠FAE=∠EDC=90°,EF=CE,
∴△AEF≌△DCE,∴AE=DC.
设AE=x cm,则DC=x cm,AD=(x+4)cm.
∵长方形ABCD的周长为32 cm,
∴2(x+x+4)=32,
解得x=6,即AE=6 cm.
9.证明:∵FB=CE,∴FB+FC=CE+FC,
即BC=EF.
∵AB∥ED,AC∥FD,
∴∠B=∠E,∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA),
∴AC=DF.
10.证明:∵AB⊥BC,EC⊥BC,
∴∠ABD=∠C=90°.
在△ABD和△BCE中,
∴△ABD≌△BCE,∴∠A=∠CBE.
∵∠CBE+∠ABE=90°,
∴∠A+∠ABE=90°,
∴AD⊥BE.
基本模型一 平移模型
常见的平移模型:
1.如图,B是线段AD的中点,BC∥DE,BC=ED.
求证:∠A=∠EBD.
2.如图,点A,B,C,D在一条直线上,AB=CD,AE∥BF,CE∥DF.
求证:AE=BF.
基本模型二 轴对称模型
常见的轴对称模型:
3.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.
求证:BE=CD.
4.如图,A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF.
求证:DE=CF.
5.[2021·淄博] 已知:在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.
求证:∠E=∠C.
基本模型三 旋转模型
常见的旋转模型:
6.[2021·泸州] 如图,AB∥CD,AD和BC相交于点O,OA=OD.求证:OB=OC.
7.[2021·苏州] 如图,在△ABC中,点E在BC边上,AE=AB.将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE.连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
基本模型四 一线三等角模型
8.如图,在长方形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥CE,且EF=CE,DE=4 cm,长方形ABCD的周长为32 cm,求AE的长.
基本模型五 综合模型
平移+对称模型: 平移+旋转模型:
9.如图,点B,F,C,E在同一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AC=DF.
10.已知:如图,AB=BC,BD=EC,AB⊥BC,EC⊥BC.求证:AD⊥BE.
答案
专题训练 全等三角形的基本模型
1.证明:∵B是线段AD的中点,∴AB=BD.
∵BC∥DE,∴∠ABC=∠D.
在△ABC和△BDE中,
∴△ABC≌△BDE(SAS),∴∠A=∠EBD.
2.证明:∵AE∥BF,∴∠A=∠FBD.
∵CE∥DF,∴∠ACE=∠D.
∵AB=CD,∴AB+BC=CD+BC,即AC=BD.
在△ACE和△BDF中,
∴△ACE≌△BDF(ASA),∴AE=BF.
3.证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°.
在△ADB和△AEC中,
∴△ADB≌△AEC(ASA),∴AB=AC.
又AD=AE,∴AB-AE=AC-AD,即BE=CD.
4.证明:∵AC=BD,∴AC+CD=BD+CD,
即AD=BC.
在△AED和△BFC中,
∴△AED≌△BFC(ASA),∴DE=CF.
5.证明:∵∠BAE=∠DAC,∴∠BAE+∠EAC=∠DAC+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,,
∴△ABC≌△ADE(SAS),∴∠E=∠C.
6.证明:∵AB∥CD,∴∠A=∠D,∠B=∠C.
在△AOB和△DOC中,
∴△AOB≌△DOC(AAS),∴OB=OC.
7.解:(1)证明:∵线段AC绕点A旋转到AF的位置, ∴AC=AF.
∵∠CAF=∠BAE,
∴∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC.
在△ABC和△AEF中,
∴△ABC≌△AEF (SAS), ∴EF=BC.
(2)∵AE=AB,∴∠AEB=∠ABC= 65°.
∵ △ABC≌△AEF,
∴∠AEF=∠ABC= 65°,
∴∠FEC=180°-∠AEB-∠AEF=180°- 65°-65°= 50°.
∵∠FGC是△EGC的一个外角,∠ACB=28°,
∴ ∠FGC=∠FEC+∠ACB =50°+ 28°=78°.
8.解:∵EF⊥CE,∴∠FEC=90°,
∴∠AEF+∠DEC=90°.
又∵∠DCE+∠DEC=90°,
∴∠AEF=∠DCE.
又∵∠FAE=∠EDC=90°,EF=CE,
∴△AEF≌△DCE,∴AE=DC.
设AE=x cm,则DC=x cm,AD=(x+4)cm.
∵长方形ABCD的周长为32 cm,
∴2(x+x+4)=32,
解得x=6,即AE=6 cm.
9.证明:∵FB=CE,∴FB+FC=CE+FC,
即BC=EF.
∵AB∥ED,AC∥FD,
∴∠B=∠E,∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA),
∴AC=DF.
10.证明:∵AB⊥BC,EC⊥BC,
∴∠ABD=∠C=90°.
在△ABD和△BCE中,
∴△ABD≌△BCE,∴∠A=∠CBE.
∵∠CBE+∠ABE=90°,
∴∠A+∠ABE=90°,
∴AD⊥BE.
同课章节目录
