湘教版数学八年级上册 第2章 三角形 本章中考演练(word版含答案)
文档属性
| 名称 | 湘教版数学八年级上册 第2章 三角形 本章中考演练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 169.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 21:29:33 | ||
图片预览


文档简介
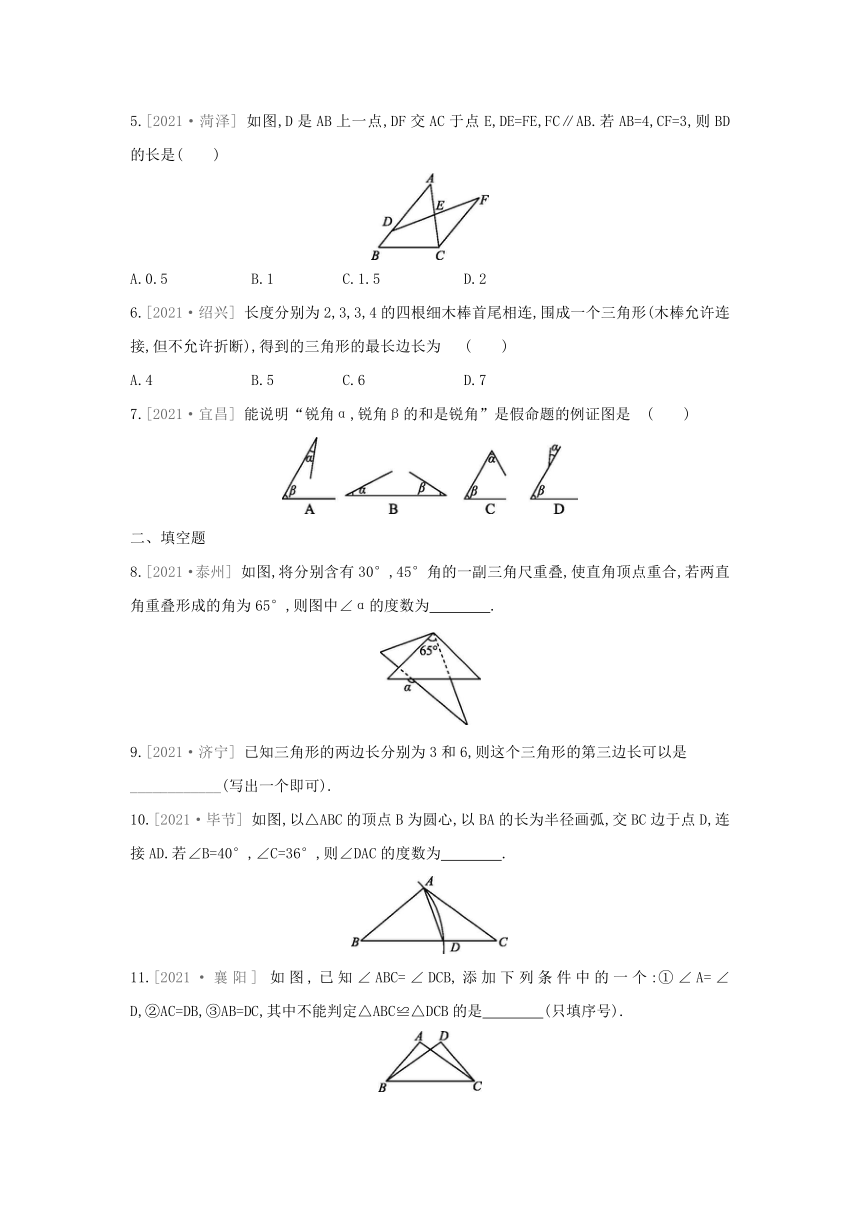
本章真题训练
一、选择题
1.[2021·毕节] 如图,在△ABC中,CD是AB边上的高,CM是AB边上的中线,点C到边AB所在直线的距离是 ( )
A.线段CA的长度 B.线段CM的长度
C.线段CD的长度 D.线段CB的长度
2.[2021·枣庄] 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为( )
A.8 B.11 C.16 D.17
3.[2021·永州改编] 下列命题是真命题的是 ( )
A.有两边和一角分别相等的两个三角形全等
B.两个锐角的和是钝角
C.如果一个角的补角等于它本身,那么这个角等于45°
D.点到直线的距离就是该点到该直线的垂线段的长度
4.[2021·甘孜州] 如图,在等腰三角形ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是 ( )
A.AD=AE B.BE=CD
C.∠ADC=∠AEB D.∠DCB=∠EBC
5.[2021·菏泽] 如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
6.[2021·绍兴] 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为 ( )
A.4 B.5 C.6 D.7
7.[2021·宜昌] 能说明“锐角α,锐角β的和是锐角”是假命题的例证图是 ( )
二、填空题
8.[2021·泰州] 如图,将分别含有30°,45°角的一副三角尺重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中∠α的度数为 .
9.[2021·济宁] 已知三角形的两边长分别为3和6,则这个三角形的第三边长可以是____________(写出一个即可).
10.[2021·毕节] 如图,以△ABC的顶点B为圆心,以BA的长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数为 .
11.[2021·襄阳] 如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB,③AB=DC,其中不能判定△ABC≌△DCB的是 (只填序号).
12.[2021·江西] 如图,CA平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
13.[2021·常德] 如图,已知△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD绕点A逆时针旋转45°得到△ACD',且D',D,B三点在同一直线上,则∠ABD的度数是 .
三、解答题
14.[2021·南通节选] 如图,点D在AB上,点E在AC上,AD=AE,∠B=∠C.求证:AB=AC.
15.[2021·青岛] 请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:∠α , 直线l及l上两点A, B(如图).求作:Rt△ABC ,使点C在直线l的上方,且∠ABC= 90° , ∠BAC =∠α.
16.[2021·南充] 如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
17.[2021·安顺] (1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
故AB,AD,DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
答案
本章真题训练
1.C
2.B ∵DE垂直平分AB,∴AE=BE,
∴△ACE的周长=AC+CE+AE=AC+CE+BE=AC+BC=5+6=11.
3.D
4.B 由全等三角形的判定“SAS”“AAS”“ASA”依次可得添加选项A,C,D都能判定△ABE≌△ACD;而添加选项B不能判定这两三个角形全等.故选B.
5.B ∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS),∴AD=CF=3.
∵AB=4,∴DB=AB-AD=4-3=1.故选B.
6.B 因为3+3=2+4,所以最长边不能是6,若是5,此时满足4-3<2+3<3+4,所以三角形的最长边长为5.故选B.
7.C 据假命题的例证即反例,需要满足条件,不满足结论;如图,分别延长∠α与∠β的两边,利用三角形外角等于与它不相邻的两个内角的和,可知∠α+∠β是钝角.故选C.
8.140°
9.答案不唯一,如4 设第三边长为x,则6-310.34° ∵∠B=40°,∠C=36°,
∴∠BAC=180°-∠B-∠C=104°.
∵AB=BD,∴∠BAD=∠ADB=(180°-∠B)÷2=70°,∴∠DAC=∠BAC-∠BAD=34°.
11.②
12.82° ∵CD=CB,∠ACD=∠ACB,CA=CA,∴△CAD≌△CAB,∴∠B=∠D.设∠ACB=α,∠B=β,则∠ACD=α,∠D=β,∠EAC为△ACD的一个外角,∴α+β=49°.在△ABC中,内角和为180°,∴α+β+∠BAC=180°,∴∠BAC=131°,∴∠BAE=∠BAC-∠EAC=82°.故答案为82°.
13.22.5° 根据题意可知△ABD≌△ACD',∴∠BAC=∠CAD'=45°,AD'=AD,
∴∠ADD'=∠AD'D==67.5°.
∵D',D,B三点在同一直线上,∴∠ABD=∠ADD'-∠BAC=22.5°.
14.证明:在△ABE和△ACD中,
∴△ABE≌△ACD(AAS),∴AB=AC.
15.解:如图所示,Rt△ABC即为所求.
16.证明:∵AB⊥BD,ED⊥BD,AC⊥CE,
∴∠ACE=∠ABC=∠CDE=90°,
∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,
∴∠ACB=∠CED.
在△ABC和△CDE中,
∴△ABC≌△CDE(ASA),∴AB=CD.
17. (1)∵AB∥DC,∴∠BAF=∠F.
∵E是BC的中点,∴CE=BE.
在△AEB和△FEC中,
∴△AEB≌△FEC,∴AB=FC.
∵AE是∠BAD的平分线,
∴∠DAF=∠BAF,∴∠DAF=∠F,
∴DF=AD.
∵DF=DC+CF,∴AD=DC+CF=DC+AB.
解:(1)AD=DC+AB
(2)AB=AF+CF.
证明:如图,延长AE交DF的延长线于点G.
∵E是BC的中点,
∴CE=BE.
∵AB∥DC,
∴∠BAE=∠G.
在△AEB和△GEC中,
∴△AEB≌△GEC,∴AB=GC.
∵AE是∠BAF的平分线,∴∠BAG=∠FAG,
∴∠FAG=∠G,则FA=FG,
∴AB=CG=FG+CF=AF+CF.
一、选择题
1.[2021·毕节] 如图,在△ABC中,CD是AB边上的高,CM是AB边上的中线,点C到边AB所在直线的距离是 ( )
A.线段CA的长度 B.线段CM的长度
C.线段CD的长度 D.线段CB的长度
2.[2021·枣庄] 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为( )
A.8 B.11 C.16 D.17
3.[2021·永州改编] 下列命题是真命题的是 ( )
A.有两边和一角分别相等的两个三角形全等
B.两个锐角的和是钝角
C.如果一个角的补角等于它本身,那么这个角等于45°
D.点到直线的距离就是该点到该直线的垂线段的长度
4.[2021·甘孜州] 如图,在等腰三角形ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是 ( )
A.AD=AE B.BE=CD
C.∠ADC=∠AEB D.∠DCB=∠EBC
5.[2021·菏泽] 如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
6.[2021·绍兴] 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为 ( )
A.4 B.5 C.6 D.7
7.[2021·宜昌] 能说明“锐角α,锐角β的和是锐角”是假命题的例证图是 ( )
二、填空题
8.[2021·泰州] 如图,将分别含有30°,45°角的一副三角尺重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中∠α的度数为 .
9.[2021·济宁] 已知三角形的两边长分别为3和6,则这个三角形的第三边长可以是____________(写出一个即可).
10.[2021·毕节] 如图,以△ABC的顶点B为圆心,以BA的长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数为 .
11.[2021·襄阳] 如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB,③AB=DC,其中不能判定△ABC≌△DCB的是 (只填序号).
12.[2021·江西] 如图,CA平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
13.[2021·常德] 如图,已知△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD绕点A逆时针旋转45°得到△ACD',且D',D,B三点在同一直线上,则∠ABD的度数是 .
三、解答题
14.[2021·南通节选] 如图,点D在AB上,点E在AC上,AD=AE,∠B=∠C.求证:AB=AC.
15.[2021·青岛] 请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:∠α , 直线l及l上两点A, B(如图).求作:Rt△ABC ,使点C在直线l的上方,且∠ABC= 90° , ∠BAC =∠α.
16.[2021·南充] 如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
17.[2021·安顺] (1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
故AB,AD,DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
答案
本章真题训练
1.C
2.B ∵DE垂直平分AB,∴AE=BE,
∴△ACE的周长=AC+CE+AE=AC+CE+BE=AC+BC=5+6=11.
3.D
4.B 由全等三角形的判定“SAS”“AAS”“ASA”依次可得添加选项A,C,D都能判定△ABE≌△ACD;而添加选项B不能判定这两三个角形全等.故选B.
5.B ∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS),∴AD=CF=3.
∵AB=4,∴DB=AB-AD=4-3=1.故选B.
6.B 因为3+3=2+4,所以最长边不能是6,若是5,此时满足4-3<2+3<3+4,所以三角形的最长边长为5.故选B.
7.C 据假命题的例证即反例,需要满足条件,不满足结论;如图,分别延长∠α与∠β的两边,利用三角形外角等于与它不相邻的两个内角的和,可知∠α+∠β是钝角.故选C.
8.140°
9.答案不唯一,如4 设第三边长为x,则6-3
∴∠BAC=180°-∠B-∠C=104°.
∵AB=BD,∴∠BAD=∠ADB=(180°-∠B)÷2=70°,∴∠DAC=∠BAC-∠BAD=34°.
11.②
12.82° ∵CD=CB,∠ACD=∠ACB,CA=CA,∴△CAD≌△CAB,∴∠B=∠D.设∠ACB=α,∠B=β,则∠ACD=α,∠D=β,∠EAC为△ACD的一个外角,∴α+β=49°.在△ABC中,内角和为180°,∴α+β+∠BAC=180°,∴∠BAC=131°,∴∠BAE=∠BAC-∠EAC=82°.故答案为82°.
13.22.5° 根据题意可知△ABD≌△ACD',∴∠BAC=∠CAD'=45°,AD'=AD,
∴∠ADD'=∠AD'D==67.5°.
∵D',D,B三点在同一直线上,∴∠ABD=∠ADD'-∠BAC=22.5°.
14.证明:在△ABE和△ACD中,
∴△ABE≌△ACD(AAS),∴AB=AC.
15.解:如图所示,Rt△ABC即为所求.
16.证明:∵AB⊥BD,ED⊥BD,AC⊥CE,
∴∠ACE=∠ABC=∠CDE=90°,
∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,
∴∠ACB=∠CED.
在△ABC和△CDE中,
∴△ABC≌△CDE(ASA),∴AB=CD.
17. (1)∵AB∥DC,∴∠BAF=∠F.
∵E是BC的中点,∴CE=BE.
在△AEB和△FEC中,
∴△AEB≌△FEC,∴AB=FC.
∵AE是∠BAD的平分线,
∴∠DAF=∠BAF,∴∠DAF=∠F,
∴DF=AD.
∵DF=DC+CF,∴AD=DC+CF=DC+AB.
解:(1)AD=DC+AB
(2)AB=AF+CF.
证明:如图,延长AE交DF的延长线于点G.
∵E是BC的中点,
∴CE=BE.
∵AB∥DC,
∴∠BAE=∠G.
在△AEB和△GEC中,
∴△AEB≌△GEC,∴AB=GC.
∵AE是∠BAF的平分线,∴∠BAG=∠FAG,
∴∠FAG=∠G,则FA=FG,
∴AB=CG=FG+CF=AF+CF.
同课章节目录
