湘教版数学八年级上册课课练:2.5全等三角形 滚动练习(word,含答案)
文档属性
| 名称 | 湘教版数学八年级上册课课练:2.5全等三角形 滚动练习(word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 138.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 17:29:21 | ||
图片预览


文档简介
[2.5]
一、选择题
1.下列判断中,结论错误的个数是 ( )
①全等三角形的面积相等;②面积相等的两个三角形全等;③全等三角形的对应边,对应角分别相等.
A.0 B.1 C.2 D.3
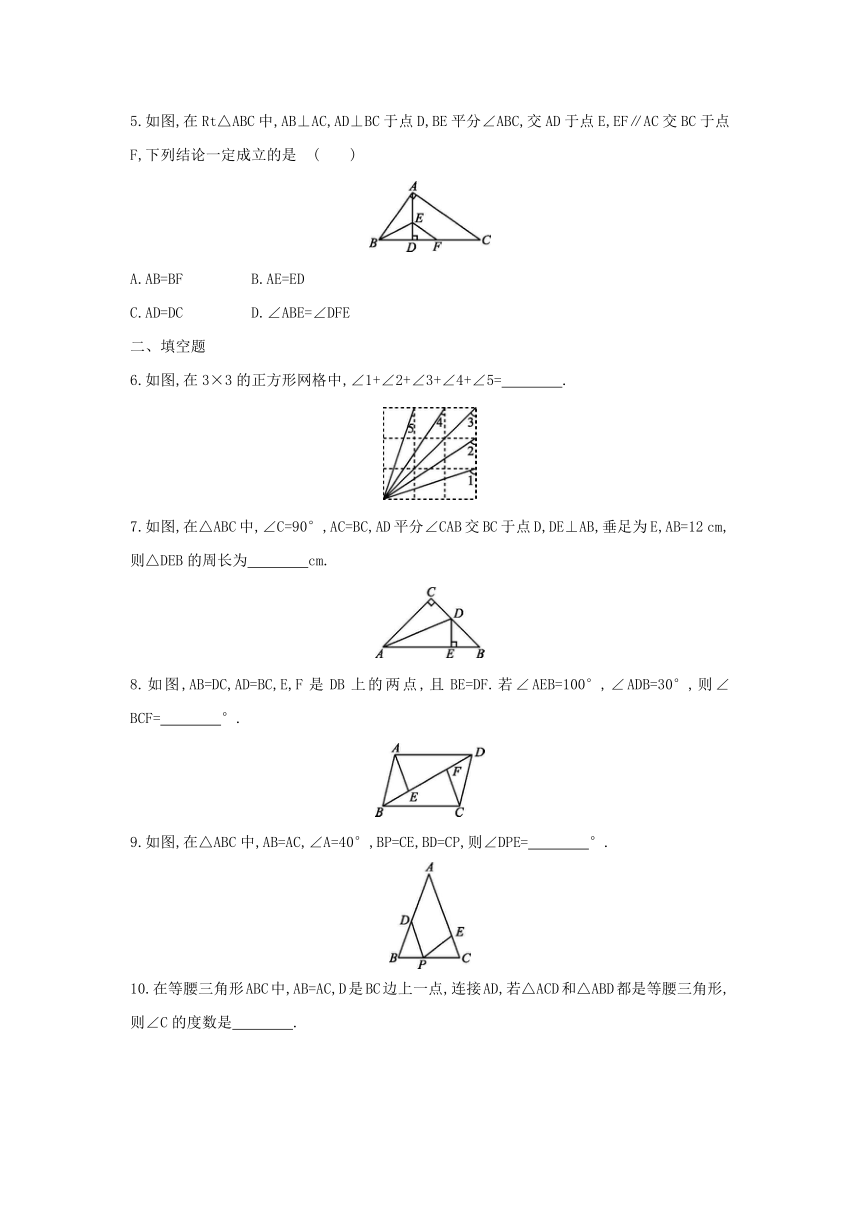
2.如图所示,∠1=∠2,∠B=∠D,△ABC翻转后与△ADE重合,说明△ABC≌△ADE,则下列结论正确的是 ( )
A.AB=AE B.AC=ED
C.∠ABC=∠AED D.∠BAC=∠DAE
3.如图所示,如果△ABD绕BD的中点旋转180°后与△CDB重合,则下面四个结论中不正确的是 ( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD
D.AD∥BC,且AD=BC
4.如图所示,已知△ABC≌△BAD,∠C和∠D对应,AC和BD对应,AB=8 cm,BD=5 cm,AD=7 cm,那么BC的长等于 ( )
A.8 cm B.5 cm
C.7 cm D.无法确定
5.如图,在Rt△ABC中,AB⊥AC,AD⊥BC于点D,BE平分∠ABC,交AD于点E,EF∥AC交BC于点F,下列结论一定成立的是 ( )
A.AB=BF B.AE=ED
C.AD=DC D.∠ABE=∠DFE
二、填空题
6.如图,在3×3的正方形网格中,∠1+∠2+∠3+∠4+∠5= .
7.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,AB=12 cm,则△DEB的周长为 cm.
8.如图,AB=DC,AD=BC,E,F是DB上的两点,且BE=DF.若∠AEB=100°,∠ADB=30°,则∠BCF= °.
9.如图,在△ABC中,AB=AC,∠A=40°,BP=CE,BD=CP,则∠DPE= °.
10.在等腰三角形ABC中,AB=AC,D是BC边上一点,连接AD,若△ACD和△ABD都是等腰三角形,则∠C的度数是 .
三、解答题
11.如图,AB=CD,AD=BC,O是BD上任意一点,过点O的直线分别交AD,BC于点M,N.求证:∠1=∠2.
12.已知:如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠ABE=∠ACE.
求证:∠BAE=∠CAE.
证明:在△AEB和△AEC中,
∴△AEB≌△AEC.(第一步)
∴∠BAE=∠CAE.(第二步)
以上证明过程是否正确 若正确,请写出每一步推理的根据;若不正确,请指出错在哪一步,并写出正确的过程.
13.如图所示,两根旗杆AC,BD相距12 m,某人从点B出发沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3 m,该人的运动速度为1 m/s,求这个人从点B到点M用了多长时间.
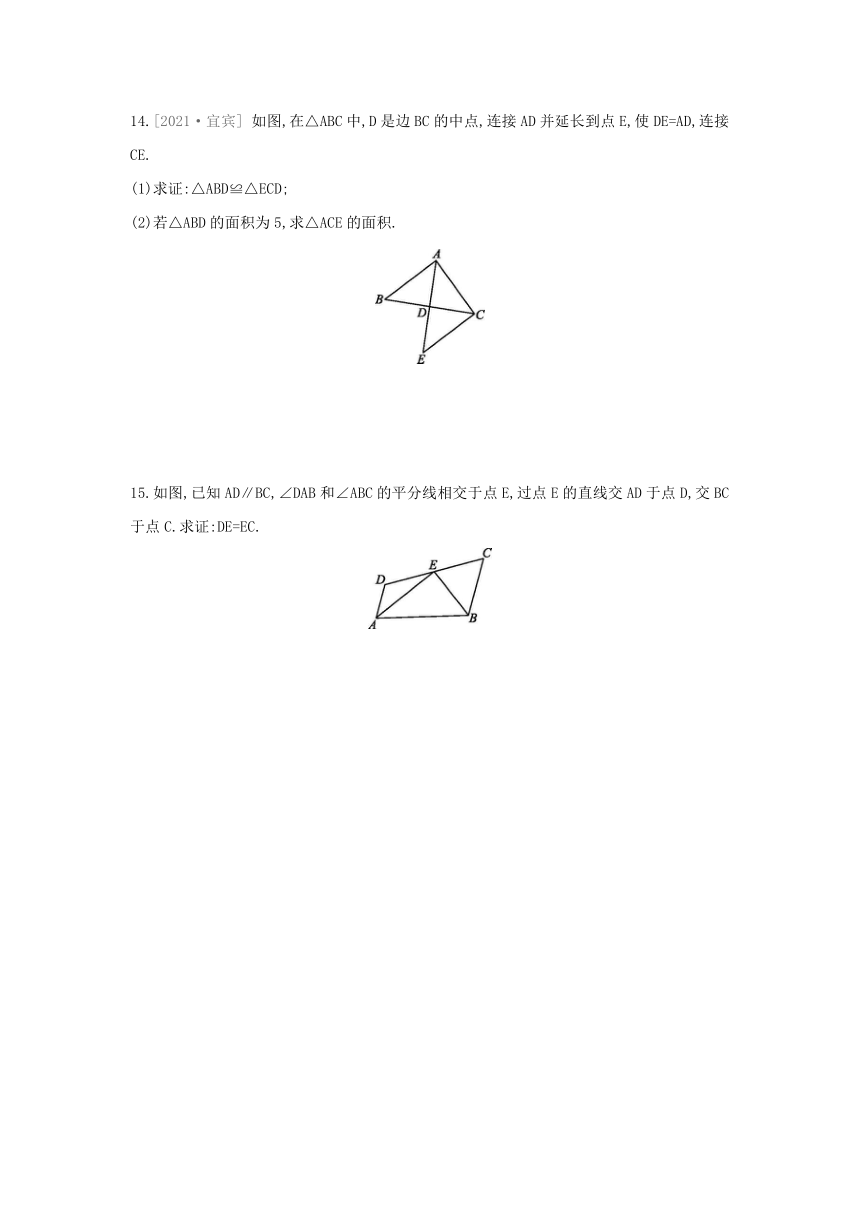
14.[2021·宜宾] 如图,在△ABC中,D是边BC的中点,连接AD并延长到点E,使DE=AD,连接CE.
(1)求证:△ABD≌△ECD;
(2)若△ABD的面积为5,求△ACE的面积.
15.如图,已知AD∥BC,∠DAB和∠ABC的平分线相交于点E,过点E的直线交AD于点D,交BC于点C.求证:DE=EC.
答案
B[2.5]
B
1.B 全等三角形的面积一定相等,但面积相等的三角形不一定是全等三角形,所以结论②错误.故选B.
2.D 因为△ABC≌△ADE,所以AB=AD,BC=DE,AC=AE,∠BAC=∠DAE,故本题中D选项正确.
3.C 由题意知△ABD≌△CDB,故△ABD与△CDB的面积相等,A项正确;因为△ABD和△CDB的三条边对应相等,故它们的周长相等,B项也正确;虽然∠A=∠C,但∠ABD和∠CBD不是对应角,不一定相等,故C项不一定成立;因为AD和BC是对应边,所以AD=BC.又因为∠ADB和∠CBD是对应角,所以∠ADB=∠CBD,故AD∥BC,故D项正确.
4.C BC与AD是对应边,全等三角形的对应边相等.
5.A ∵∠BAD+∠ABD=90°,∠ABD+∠C=90°,∴∠BAD=∠C(同角的余角相等).又∵EF∥AC,∴∠BFE=∠C,∴∠BAD=∠BFE.又∵BE平分∠ABC,∴∠ABE=∠FBE.又BE=BE,∴△ABE≌△FBE,∴AB=BF.
6.225° 观察图形可知∠1与∠5所在的三角形全等,这两角互余,∠2与∠4所在的三角形全等,这两角互余,∠3=45°,∴∠1+∠5=90°,∠2+∠4=90°,∠3=45°,∴∠1+∠2+∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)+∠3=225°.
7.12 ∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴∠CAD=∠BAD,∠C=∠AED.
在△CAD和△EAD中,
∴△CAD≌△EAD,∴AC=AE,CD=ED.
∵AC=BC,∴BC=AE,
∴△DEB的周长=DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=12 cm.
8.70 ∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB,∴∠CBD=∠ADB=30°,∠ABD=∠CDB.又AB=CD,BE=DF,
∴△ABE≌△CDF,∴∠DFC=∠AEB=100°,
∴∠BCF=∠DFC-∠CBF=100°-30°=70°.
9.70 ∵AB=AC,∠A=40°,
∴∠DBP=∠ECP=70°.
又∵BP=CE,BD=CP,∴△DBP≌△PCE,
∴∠BDP=∠EPC.
又∵∠DBP=70°,∴∠DPB+∠BDP=110°,
∴∠DPE=180°-(∠DPB+∠EPC)=180°-(∠DPB+∠BDP)=70°.
10.36°或45°
11.证明:在△ABD和△CDB中,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,∴AD∥BC,
故∠1=∠2.
12.解:以上证明过程不正确,错在第一步.
正确的证明过程:
在△EBC中,∵EB=EC,∴∠EBC=∠ECB.
又∵∠ABE=∠ACE,
∴∠ABC=∠ACB,
∴AB=AC.
在△AEB和△AEC中,
∴△AEB≌△AEC,
∴∠BAE=∠CAE.
13.解:∵∠CMD=90°,
∴∠CMA+∠BMD=90°.
∵∠CAM=90°,
∴∠CMA+∠ACM=90°,
∴∠ACM=∠BMD.
在△ACM和△BMD中,
∴△ACM≌△BMD(AAS),
∴AC=BM=3 m,
∴这个人从点B到点M用的时间为3÷1=3(s).
14.解:(1)证明:∵D是边BC的中点,
∴BD=CD.
在△ABD和△ECD中,
∴△ABD≌△ECD(SAS).
(2)在△ABC中,D是边BC的中点,
∴S△ABD=S△ACD.
∵△ABD≌△ECD,
∴S△ABD=S△ECD.
∵S△ABD=5,
∴S△ACE=S△ACD+S△ECD=5+5=10.
答:△ACE的面积为10.
15.证明:在AB上取一点F,使AF=AD,连接EF,如图.
因为AE平分∠DAB,
所以∠DAE=∠FAE.
在△ADE和△AFE中,
所以△ADE≌△AFE,
所以DE=FE,∠D=∠AFE.
又因为AD∥BC,所以∠D+∠C=180°.
又因为∠EFB+∠AFE=180°,
所以∠C=∠EFB.
因为BE平分∠ABC,所以∠FBE=∠CBE.
在△EFB和△ECB中,
所以△EFB≌△ECB,
所以EC=EF,故DE=EC.
一、选择题
1.下列判断中,结论错误的个数是 ( )
①全等三角形的面积相等;②面积相等的两个三角形全等;③全等三角形的对应边,对应角分别相等.
A.0 B.1 C.2 D.3
2.如图所示,∠1=∠2,∠B=∠D,△ABC翻转后与△ADE重合,说明△ABC≌△ADE,则下列结论正确的是 ( )
A.AB=AE B.AC=ED
C.∠ABC=∠AED D.∠BAC=∠DAE
3.如图所示,如果△ABD绕BD的中点旋转180°后与△CDB重合,则下面四个结论中不正确的是 ( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD
D.AD∥BC,且AD=BC
4.如图所示,已知△ABC≌△BAD,∠C和∠D对应,AC和BD对应,AB=8 cm,BD=5 cm,AD=7 cm,那么BC的长等于 ( )
A.8 cm B.5 cm
C.7 cm D.无法确定
5.如图,在Rt△ABC中,AB⊥AC,AD⊥BC于点D,BE平分∠ABC,交AD于点E,EF∥AC交BC于点F,下列结论一定成立的是 ( )
A.AB=BF B.AE=ED
C.AD=DC D.∠ABE=∠DFE
二、填空题
6.如图,在3×3的正方形网格中,∠1+∠2+∠3+∠4+∠5= .
7.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,AB=12 cm,则△DEB的周长为 cm.
8.如图,AB=DC,AD=BC,E,F是DB上的两点,且BE=DF.若∠AEB=100°,∠ADB=30°,则∠BCF= °.
9.如图,在△ABC中,AB=AC,∠A=40°,BP=CE,BD=CP,则∠DPE= °.
10.在等腰三角形ABC中,AB=AC,D是BC边上一点,连接AD,若△ACD和△ABD都是等腰三角形,则∠C的度数是 .
三、解答题
11.如图,AB=CD,AD=BC,O是BD上任意一点,过点O的直线分别交AD,BC于点M,N.求证:∠1=∠2.
12.已知:如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠ABE=∠ACE.
求证:∠BAE=∠CAE.
证明:在△AEB和△AEC中,
∴△AEB≌△AEC.(第一步)
∴∠BAE=∠CAE.(第二步)
以上证明过程是否正确 若正确,请写出每一步推理的根据;若不正确,请指出错在哪一步,并写出正确的过程.
13.如图所示,两根旗杆AC,BD相距12 m,某人从点B出发沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3 m,该人的运动速度为1 m/s,求这个人从点B到点M用了多长时间.
14.[2021·宜宾] 如图,在△ABC中,D是边BC的中点,连接AD并延长到点E,使DE=AD,连接CE.
(1)求证:△ABD≌△ECD;
(2)若△ABD的面积为5,求△ACE的面积.
15.如图,已知AD∥BC,∠DAB和∠ABC的平分线相交于点E,过点E的直线交AD于点D,交BC于点C.求证:DE=EC.
答案
B[2.5]
B
1.B 全等三角形的面积一定相等,但面积相等的三角形不一定是全等三角形,所以结论②错误.故选B.
2.D 因为△ABC≌△ADE,所以AB=AD,BC=DE,AC=AE,∠BAC=∠DAE,故本题中D选项正确.
3.C 由题意知△ABD≌△CDB,故△ABD与△CDB的面积相等,A项正确;因为△ABD和△CDB的三条边对应相等,故它们的周长相等,B项也正确;虽然∠A=∠C,但∠ABD和∠CBD不是对应角,不一定相等,故C项不一定成立;因为AD和BC是对应边,所以AD=BC.又因为∠ADB和∠CBD是对应角,所以∠ADB=∠CBD,故AD∥BC,故D项正确.
4.C BC与AD是对应边,全等三角形的对应边相等.
5.A ∵∠BAD+∠ABD=90°,∠ABD+∠C=90°,∴∠BAD=∠C(同角的余角相等).又∵EF∥AC,∴∠BFE=∠C,∴∠BAD=∠BFE.又∵BE平分∠ABC,∴∠ABE=∠FBE.又BE=BE,∴△ABE≌△FBE,∴AB=BF.
6.225° 观察图形可知∠1与∠5所在的三角形全等,这两角互余,∠2与∠4所在的三角形全等,这两角互余,∠3=45°,∴∠1+∠5=90°,∠2+∠4=90°,∠3=45°,∴∠1+∠2+∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)+∠3=225°.
7.12 ∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴∠CAD=∠BAD,∠C=∠AED.
在△CAD和△EAD中,
∴△CAD≌△EAD,∴AC=AE,CD=ED.
∵AC=BC,∴BC=AE,
∴△DEB的周长=DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=12 cm.
8.70 ∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB,∴∠CBD=∠ADB=30°,∠ABD=∠CDB.又AB=CD,BE=DF,
∴△ABE≌△CDF,∴∠DFC=∠AEB=100°,
∴∠BCF=∠DFC-∠CBF=100°-30°=70°.
9.70 ∵AB=AC,∠A=40°,
∴∠DBP=∠ECP=70°.
又∵BP=CE,BD=CP,∴△DBP≌△PCE,
∴∠BDP=∠EPC.
又∵∠DBP=70°,∴∠DPB+∠BDP=110°,
∴∠DPE=180°-(∠DPB+∠EPC)=180°-(∠DPB+∠BDP)=70°.
10.36°或45°
11.证明:在△ABD和△CDB中,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,∴AD∥BC,
故∠1=∠2.
12.解:以上证明过程不正确,错在第一步.
正确的证明过程:
在△EBC中,∵EB=EC,∴∠EBC=∠ECB.
又∵∠ABE=∠ACE,
∴∠ABC=∠ACB,
∴AB=AC.
在△AEB和△AEC中,
∴△AEB≌△AEC,
∴∠BAE=∠CAE.
13.解:∵∠CMD=90°,
∴∠CMA+∠BMD=90°.
∵∠CAM=90°,
∴∠CMA+∠ACM=90°,
∴∠ACM=∠BMD.
在△ACM和△BMD中,
∴△ACM≌△BMD(AAS),
∴AC=BM=3 m,
∴这个人从点B到点M用的时间为3÷1=3(s).
14.解:(1)证明:∵D是边BC的中点,
∴BD=CD.
在△ABD和△ECD中,
∴△ABD≌△ECD(SAS).
(2)在△ABC中,D是边BC的中点,
∴S△ABD=S△ACD.
∵△ABD≌△ECD,
∴S△ABD=S△ECD.
∵S△ABD=5,
∴S△ACE=S△ACD+S△ECD=5+5=10.
答:△ACE的面积为10.
15.证明:在AB上取一点F,使AF=AD,连接EF,如图.
因为AE平分∠DAB,
所以∠DAE=∠FAE.
在△ADE和△AFE中,
所以△ADE≌△AFE,
所以DE=FE,∠D=∠AFE.
又因为AD∥BC,所以∠D+∠C=180°.
又因为∠EFB+∠AFE=180°,
所以∠C=∠EFB.
因为BE平分∠ABC,所以∠FBE=∠CBE.
在△EFB和△ECB中,
所以△EFB≌△ECB,
所以EC=EF,故DE=EC.
同课章节目录
