湘教版数学八年级上册2.1-2.4线段的垂直平分线 滚动练习(word版含答案)
文档属性
| 名称 | 湘教版数学八年级上册2.1-2.4线段的垂直平分线 滚动练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 130.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 21:36:19 | ||
图片预览


文档简介
[2.1~2.4]
一、选择题
1.如图所示的图形中,三角形的个数是 ( )
A.2 B.3 C.4 D.5
2.[2021·杭州] 在△ABC中,若一个内角等于另外两个内角的差,则 ( )
A.必有一个内角等于30°
B.必有一个内角等于45°
C.必有一个内角等于60°
D.必有一个内角等于90°
3.已知下列命题:①过一点有且只有一条直线与已知直线平行;②同旁内角互补;③等腰三角形的高、角平分线、中线相互重合;④如果一个数的平方等于这个数本身,那么这个数一定是0.其中假命题的个数为 ( )
A.1 B.2 C.3 D.4
4.某同学手里拿着长为3和2的两根木棍,想要找一根木棍,用它们围成一个三角形,那么他所找的满足条件的木棍的整数长可以是 ( )
A.1,3,5 B.1,2,3 C.2,3,4 D.3,4,5
5.在△ABC中,2(∠A+∠C)=3∠B,则∠B的外角的度数为 ( )
A.36° B.72° C.108° D.144°
6.如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠EAC的度数是 ( )
A.40° B.65° C.70° D.75°
7.[2021·湘西州] 已知∠AOB,作∠AOB的平分线OM,在射线OM上截取线段OC,分别以点O,C为圆心,大于OC的长为半径画弧,两弧相交于点E,F,画直线EF,分别交OA于点D,交OB于点G.那么△ODG一定是 ( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
二、填空题
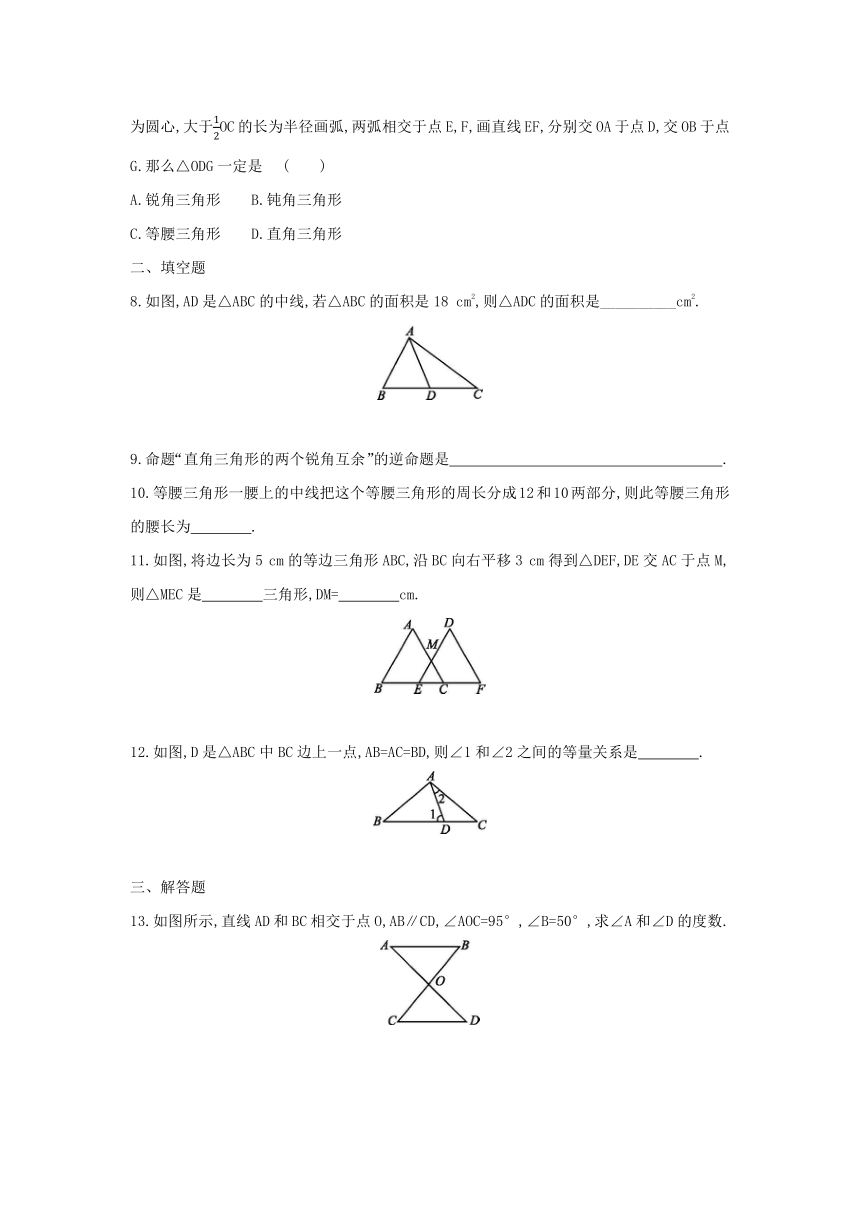
8.如图,AD是△ABC的中线,若△ABC的面积是18 cm2,则△ADC的面积是__________cm2.
9.命题“直角三角形的两个锐角互余”的逆命题是 .
10.等腰三角形一腰上的中线把这个等腰三角形的周长分成12和10两部分,则此等腰三角形的腰长为 .
11.如图,将边长为5 cm的等边三角形ABC,沿BC向右平移3 cm得到△DEF,DE交AC于点M,则△MEC是 三角形,DM= cm.
12.如图,D是△ABC中BC边上一点,AB=AC=BD,则∠1和∠2之间的等量关系是 .
三、解答题
13.如图所示,直线AD和BC相交于点O,AB∥CD,∠AOC=95°,∠B=50°,求∠A和∠D的度数.
14.如图,△ABC的三条角平分线AD,BE,CF交于一点O,过点O作OG⊥BC于点G.
求证:∠BOD=∠COG.
15.求证:等腰三角形腰上的高与底边的夹角等于顶角的一半.
16.如图,在△ABC中,DE是AC的垂直平分线,AE=4 cm,△ABD的周长为14 cm,求△ABC的周长.
17.如图,已知D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,已知AF∥BC.
(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
18.如图,P是等边三角形ABC内一点,将△APC绕点C顺时针旋转60°得到△BDC,连接PD,BP.
(1)求证:△DPC是等边三角形;
(2)当∠APC=150°时,试判断△DPB的形状,并说明理由;
(3)当∠APB=100°,且△DPB是等腰三角形,求∠APC的度数.
答案
B[2.1~2.4]
B
1.D △ABE,△DEC,△BEC,△ABC,△DBC,共5个.
2.D
3.D
4.C 设他所找的木棍长为x.由题意,得3-25.C ∵∠A+∠B+∠C=180°,∴2(∠A+∠B+∠C)=360°.∵2(∠A+∠C)=3∠B,∴∠B=72°,∴∠B的外角的度数是180°-∠B=108°.
6.D ∵BD平分∠ABC,∴∠ABD=∠DBC.∵BD∥AE,∴∠BAE=∠ABD,∠E=∠DBC,∴∠BAE=∠E=35°,∠ABC=70°.∵AB=AC,∴∠ABC=∠C=70°,∴∠BAC=180°-70°-70°=40°,∴∠EAC=∠BAE+∠BAC=35°+40°=75°.
7.C 如图,∵OM平分∠AOB,
∴∠AOC=∠BOC,由题可知,EF垂直平分OC,
∴∠OND=∠ONG=90°,∴∠ODN=∠OGN,则OD=OG,∴△ODG是等腰三角形.故选C.
8.9 S△ADC=S△ABC÷2=18÷2=9(cm2).
9. 如果一个三角形的两个锐角互余,那么这个三角形是直角三角形
10.8或 设此等腰三角形的腰长为x,底边长为y.依题意有或所以x=8或x=.若x=8,则y=6,此时三边长分别为8,8,6,能组成三角形;若x=,则y=,此时三边长分别为,,,也能组成三角形.
综上可得,此等腰三角形的腰长为8或.
11.等边 3
12.3∠1-∠2=180° ∵AB=AC,
∴∠B=∠C.∵AB=BD,∴∠BAD=∠1.根据外角定理,得∠1=∠2+∠C=∠2+∠B,所以∠B=∠1-∠2.在△ABD中,∠B+∠1+∠BAD=180°,∴∠1-∠2+2∠1=180°,即3∠1-∠2=180°.
13.解:∵∠AOC是△AOB的一个外角,
∴∠AOC=∠A+∠B(三角形的一个外角等于和它不相邻的两个内角的和).
∵∠AOC=95°,∠B=50°,
∴∠A=∠AOC-∠B=95°-50°=45°.
∵AB∥CD,
∴∠D=∠A(两直线平行,内错角相等),
∴∠D=45°.
14.证明:∵O为△ABC的角平分线的交点,
∴∠ABO=∠ABC,∠BAO=∠BAC,∠OCD=∠ACB,
∴∠AOB=180°-(∠ABC+∠BAC)=180°-(180°-∠ACB)=90°+∠ACB,
∴∠BOD=180°-∠AOB=90°-∠ACB=90°-∠OCD.
∵OG⊥BC,
∴∠COG=90°-∠OCD,
∴∠BOD=∠COG.
15.解:已知:如图,在△ABC中,AB=AC,BD⊥AC.
求证:∠CBD= ∠A.
证明:∵BD⊥AC,
∴∠BDC=∠BDA=90°,
∴∠1=90°-∠C,∠A+∠2=90°,
∴∠1=90°-∠C=∠A+∠2-∠C①.
又∵AB=AC,∴∠ABC=∠C,
∴∠2=∠ABC-∠1=∠C-∠1②.
将②代入①,得∠1=∠A+∠C-∠1-∠C,
即2∠1=∠A,
即∠CBD=∠A.
16.解:因为DE是AC的垂直平分线,
所以AD=CD,E是AC的中点,
所以AE=CE.
因为△ABD的周长为14 cm,
即AB+BD+AD=14 cm.
所以△ABC的周长为AB+BC+AC=AB+BD+CD+2AE=AB+BD+AD+2AE=14+8=22(cm).
17.解:(1)证明:∵AF平分∠DAC,∴∠DAF=∠CAF. ∵AF∥BC,∴∠DAF=∠B,∠CAF=∠ACB,∴∠B=∠ACB,∴△ABC是等腰三角形.
(2)∵∠B=40°,∴∠ACB=∠B=40°,∴∠ACE=140°.
∵CG平分∠ACE,
∴∠ACG=∠ACE=70°.
∵AF∥BC,
∴∠AGC=180°-∠BCG=180°-40°-70°=70°.
18.解:(1)证明:由旋转的性质,得 PC=DC,∠PCA=∠DCB,∴∠PCD=∠ACB.∵在等边三角形ABC中,∠ACB=60°,∴∠PCD=60°,∴△DPC是等边三角形.
(2)△DPB是直角三角形.理由:由旋转得∠BDC=∠APC=150°.又∵△DPC是等边三角形,∴∠PDC=60°,∴∠BDP=∠BDC-∠PDC=90°,∴△DPB是直角三角形.
(3)设∠APC=x,则∠BPD=200°-x,∠BDP=x-60°.
①若PD=PB,则(200°-x)+2(x-60°)=180°,∴x=100°;
②若PD=DB,则2(200°-x)+(x-60°)=180°,∴x=160°;
③若PB=DB,则200°-x=x-60°,∴x=130°.
综上,∠APC的度数为100°或160°或130°.
一、选择题
1.如图所示的图形中,三角形的个数是 ( )
A.2 B.3 C.4 D.5
2.[2021·杭州] 在△ABC中,若一个内角等于另外两个内角的差,则 ( )
A.必有一个内角等于30°
B.必有一个内角等于45°
C.必有一个内角等于60°
D.必有一个内角等于90°
3.已知下列命题:①过一点有且只有一条直线与已知直线平行;②同旁内角互补;③等腰三角形的高、角平分线、中线相互重合;④如果一个数的平方等于这个数本身,那么这个数一定是0.其中假命题的个数为 ( )
A.1 B.2 C.3 D.4
4.某同学手里拿着长为3和2的两根木棍,想要找一根木棍,用它们围成一个三角形,那么他所找的满足条件的木棍的整数长可以是 ( )
A.1,3,5 B.1,2,3 C.2,3,4 D.3,4,5
5.在△ABC中,2(∠A+∠C)=3∠B,则∠B的外角的度数为 ( )
A.36° B.72° C.108° D.144°
6.如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠EAC的度数是 ( )
A.40° B.65° C.70° D.75°
7.[2021·湘西州] 已知∠AOB,作∠AOB的平分线OM,在射线OM上截取线段OC,分别以点O,C为圆心,大于OC的长为半径画弧,两弧相交于点E,F,画直线EF,分别交OA于点D,交OB于点G.那么△ODG一定是 ( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
二、填空题
8.如图,AD是△ABC的中线,若△ABC的面积是18 cm2,则△ADC的面积是__________cm2.
9.命题“直角三角形的两个锐角互余”的逆命题是 .
10.等腰三角形一腰上的中线把这个等腰三角形的周长分成12和10两部分,则此等腰三角形的腰长为 .
11.如图,将边长为5 cm的等边三角形ABC,沿BC向右平移3 cm得到△DEF,DE交AC于点M,则△MEC是 三角形,DM= cm.
12.如图,D是△ABC中BC边上一点,AB=AC=BD,则∠1和∠2之间的等量关系是 .
三、解答题
13.如图所示,直线AD和BC相交于点O,AB∥CD,∠AOC=95°,∠B=50°,求∠A和∠D的度数.
14.如图,△ABC的三条角平分线AD,BE,CF交于一点O,过点O作OG⊥BC于点G.
求证:∠BOD=∠COG.
15.求证:等腰三角形腰上的高与底边的夹角等于顶角的一半.
16.如图,在△ABC中,DE是AC的垂直平分线,AE=4 cm,△ABD的周长为14 cm,求△ABC的周长.
17.如图,已知D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,已知AF∥BC.
(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
18.如图,P是等边三角形ABC内一点,将△APC绕点C顺时针旋转60°得到△BDC,连接PD,BP.
(1)求证:△DPC是等边三角形;
(2)当∠APC=150°时,试判断△DPB的形状,并说明理由;
(3)当∠APB=100°,且△DPB是等腰三角形,求∠APC的度数.
答案
B[2.1~2.4]
B
1.D △ABE,△DEC,△BEC,△ABC,△DBC,共5个.
2.D
3.D
4.C 设他所找的木棍长为x.由题意,得3-2
6.D ∵BD平分∠ABC,∴∠ABD=∠DBC.∵BD∥AE,∴∠BAE=∠ABD,∠E=∠DBC,∴∠BAE=∠E=35°,∠ABC=70°.∵AB=AC,∴∠ABC=∠C=70°,∴∠BAC=180°-70°-70°=40°,∴∠EAC=∠BAE+∠BAC=35°+40°=75°.
7.C 如图,∵OM平分∠AOB,
∴∠AOC=∠BOC,由题可知,EF垂直平分OC,
∴∠OND=∠ONG=90°,∴∠ODN=∠OGN,则OD=OG,∴△ODG是等腰三角形.故选C.
8.9 S△ADC=S△ABC÷2=18÷2=9(cm2).
9. 如果一个三角形的两个锐角互余,那么这个三角形是直角三角形
10.8或 设此等腰三角形的腰长为x,底边长为y.依题意有或所以x=8或x=.若x=8,则y=6,此时三边长分别为8,8,6,能组成三角形;若x=,则y=,此时三边长分别为,,,也能组成三角形.
综上可得,此等腰三角形的腰长为8或.
11.等边 3
12.3∠1-∠2=180° ∵AB=AC,
∴∠B=∠C.∵AB=BD,∴∠BAD=∠1.根据外角定理,得∠1=∠2+∠C=∠2+∠B,所以∠B=∠1-∠2.在△ABD中,∠B+∠1+∠BAD=180°,∴∠1-∠2+2∠1=180°,即3∠1-∠2=180°.
13.解:∵∠AOC是△AOB的一个外角,
∴∠AOC=∠A+∠B(三角形的一个外角等于和它不相邻的两个内角的和).
∵∠AOC=95°,∠B=50°,
∴∠A=∠AOC-∠B=95°-50°=45°.
∵AB∥CD,
∴∠D=∠A(两直线平行,内错角相等),
∴∠D=45°.
14.证明:∵O为△ABC的角平分线的交点,
∴∠ABO=∠ABC,∠BAO=∠BAC,∠OCD=∠ACB,
∴∠AOB=180°-(∠ABC+∠BAC)=180°-(180°-∠ACB)=90°+∠ACB,
∴∠BOD=180°-∠AOB=90°-∠ACB=90°-∠OCD.
∵OG⊥BC,
∴∠COG=90°-∠OCD,
∴∠BOD=∠COG.
15.解:已知:如图,在△ABC中,AB=AC,BD⊥AC.
求证:∠CBD= ∠A.
证明:∵BD⊥AC,
∴∠BDC=∠BDA=90°,
∴∠1=90°-∠C,∠A+∠2=90°,
∴∠1=90°-∠C=∠A+∠2-∠C①.
又∵AB=AC,∴∠ABC=∠C,
∴∠2=∠ABC-∠1=∠C-∠1②.
将②代入①,得∠1=∠A+∠C-∠1-∠C,
即2∠1=∠A,
即∠CBD=∠A.
16.解:因为DE是AC的垂直平分线,
所以AD=CD,E是AC的中点,
所以AE=CE.
因为△ABD的周长为14 cm,
即AB+BD+AD=14 cm.
所以△ABC的周长为AB+BC+AC=AB+BD+CD+2AE=AB+BD+AD+2AE=14+8=22(cm).
17.解:(1)证明:∵AF平分∠DAC,∴∠DAF=∠CAF. ∵AF∥BC,∴∠DAF=∠B,∠CAF=∠ACB,∴∠B=∠ACB,∴△ABC是等腰三角形.
(2)∵∠B=40°,∴∠ACB=∠B=40°,∴∠ACE=140°.
∵CG平分∠ACE,
∴∠ACG=∠ACE=70°.
∵AF∥BC,
∴∠AGC=180°-∠BCG=180°-40°-70°=70°.
18.解:(1)证明:由旋转的性质,得 PC=DC,∠PCA=∠DCB,∴∠PCD=∠ACB.∵在等边三角形ABC中,∠ACB=60°,∴∠PCD=60°,∴△DPC是等边三角形.
(2)△DPB是直角三角形.理由:由旋转得∠BDC=∠APC=150°.又∵△DPC是等边三角形,∴∠PDC=60°,∴∠BDP=∠BDC-∠PDC=90°,∴△DPB是直角三角形.
(3)设∠APC=x,则∠BPD=200°-x,∠BDP=x-60°.
①若PD=PB,则(200°-x)+2(x-60°)=180°,∴x=100°;
②若PD=DB,则2(200°-x)+(x-60°)=180°,∴x=160°;
③若PB=DB,则200°-x=x-60°,∴x=130°.
综上,∠APC的度数为100°或160°或130°.
同课章节目录
