2022-2023学年人教版八年级数学上册 11.1.1三角形的边 课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 11.1.1三角形的边 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
人教版数学八年级上册
第11.1.1三角形的边
情境引入
情境引入
在上面图片中你发现了哪些图形呢?
三角形
生活中还有许多使用三角形的实例,你能举例吗?
互动新授
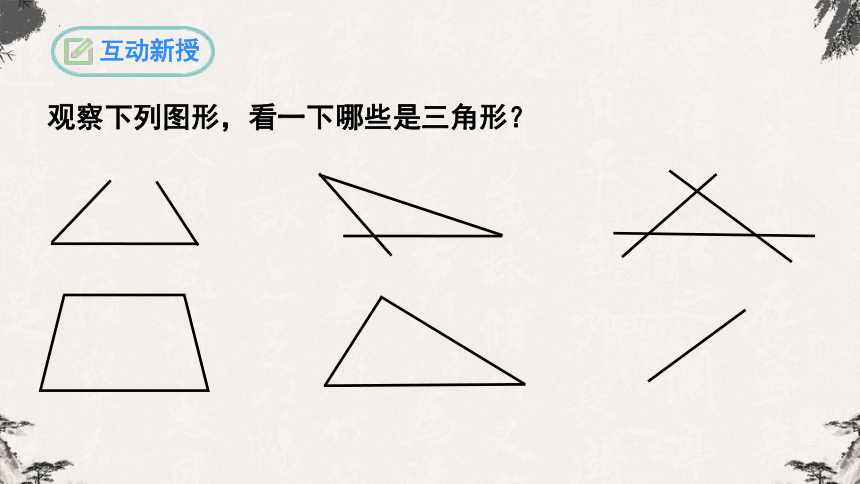
观察下列图形,看一下哪些是三角形?
互动新授
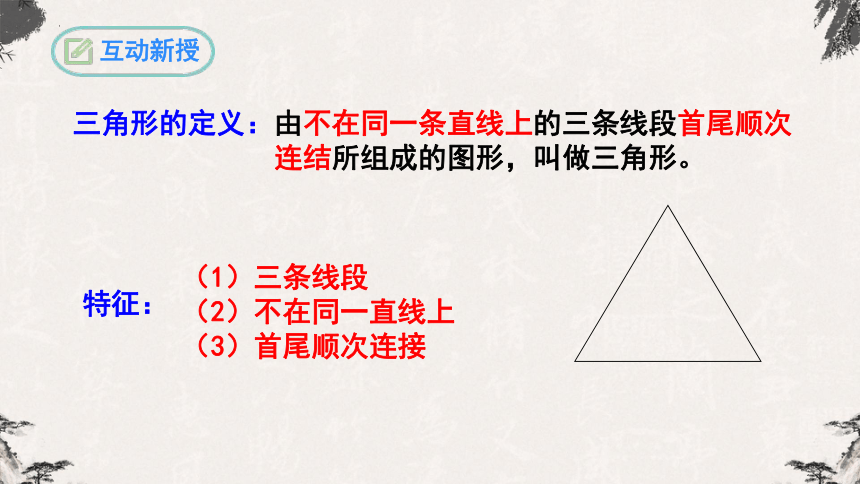
三角形的定义:
由不在同一条直线上的三条线段首尾顺次连结所组成的图形,叫做三角形。
特征:
(1)三条线段
(2)不在同一直线上
(3)首尾顺次连接
A
B
C
互动新授
三角形表示方法:
三角形的顶点:
三角形相邻两边的公共端点叫做三角形的顶点。
顶点是A,B,C的三角形记作△ABC,读作“三角形ABC”.
顶点
通常:顶点A所对的边BC用a表示,顶点B所对的边CA用b表示,顶点C所对的边AB用c表示.
三角形的线段:
分别用AB, BC, AC表示
a
b
c
三角形的角:
互动新授
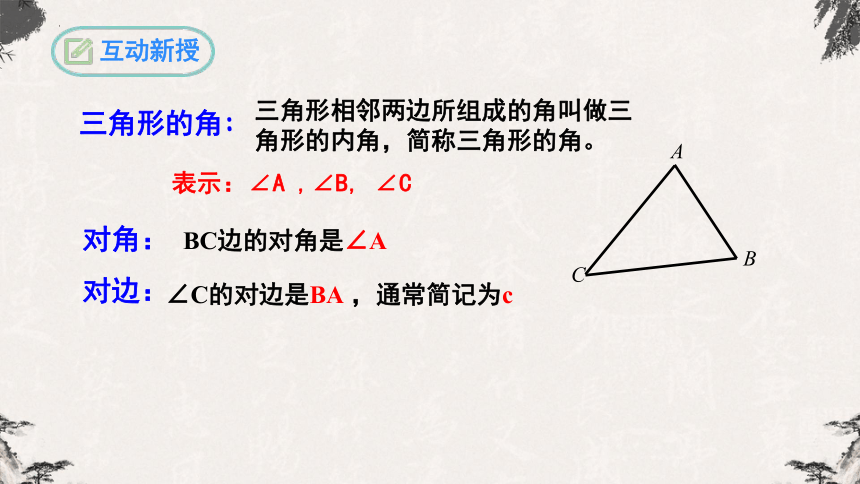
三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
A
B
C
对角:
对边:
BC边的对角是∠A
∠C的对边是BA ,通常简记为c
表示:∠A ,∠B, ∠C
1.图中有几个三角形?如何用符号表示这些三角形?以点E为顶点的三角形有哪几个?以∠D为角的三角形有哪些?
A
C
E
小试牛刀
共有5个三角形,
分别为:△ABE,△ABC,△BCD, △BCE,△CED.
以点E为顶点的三角形有3个,
分别为:△EAB,△ECD,△EBC.
以点E∠D为角的三角形有2个,
分别为:△DEC,△DBC
D
B
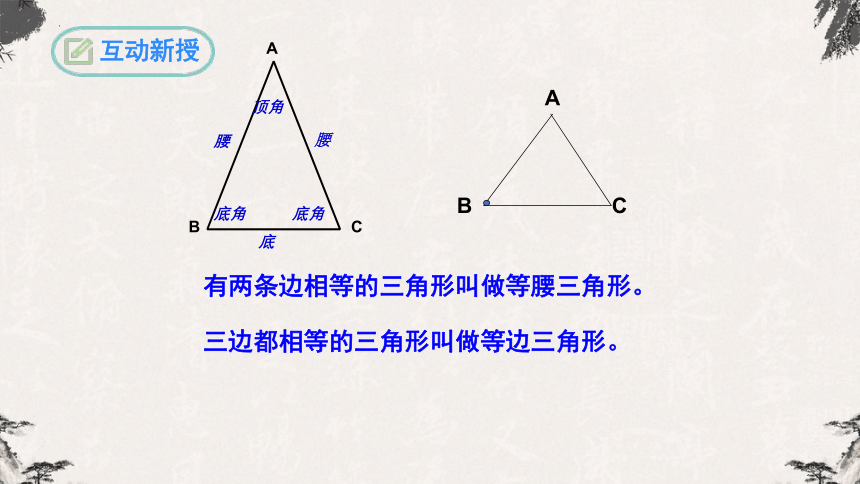
有两条边相等的三角形叫做等腰三角形。
三边都相等的三角形叫做等边三角形。
腰
腰
底
顶角
底角
底角
A
B
C
A
B
C
互动新授
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
三边都不相等的三角形
三角形的分类
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三边都不相等的三角形
等腰三角形
等边三角形
总结归纳
合作探究
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?能证明你的结论吗?
A
C
B
路线1:从点B到点A,再从点A到点C,长度:BA+AC.
路线2:从点B直接到点C,长度:BC.
BA+AC 和BC 的大小关系如何?
理由:“两点之间,线段最短”
可得:BA+AC>BC.
从B到A呢?有几条线路可以选择?各条线路的长有什么关系?
小结归纳
A
C
B
AC+CB>AB
BA+AC>BC
CB+BA>CA
BA>BC-AC
AC>AB-CB
CB>CA-BA
三角形的三边关系:
1、三角形两边之和大于第三边;
2、三角形两边之差小于第三边.
例1:判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm,9cm,5cm (2) 6cm,7cm,13cm
(3)5cm,7cm,9cm
典例精析
解:(1)不能,因为3cm+5cm<9cm,不满足两边之和大于第三边.
(2)不能,因为6cm+7cm=13cm,不满足两边之和大于第三边.
(3)能,因为5cm+7cm>9cm,5cm+9cm>7cm,7cm+9cm>5cm,或9cm-5cm<7cm,9cm-7cm<5cm,7cm-5cm<9cm.
有没有更简便的方法呢?
归纳:判断三条线段是否可以构成三角形,只需判断“两条较短的线段之和大于第三条”即可.
典例精析
例2:用一条长18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
解:(1)设底边长为xcm,则腰长为2xcm.
由题可得: x+2x+2x=18,
解得x=3.6.
所以,三边长分别为3.6cm,7.2cm,7.2cm.
例2:用一条长18cm的细绳围成一个等腰三角形.
(2)能围成有一边的长是4cm的等腰三角形吗?为什么?
典例精析
(2)因为长为4cm的边可能是腰,也可能是底边,所以要分情况讨论.
第一种情况:如果4cm的边为底边,设腰长为xcm,则,4+x+x=18,
解得:x=7.
第二种情况:如果4cm的边为腰长,设底边长为xcm,则,4+4+x=18,
解得:x=10.
因为4+4<10,不符合三角形两边的和大于第三边,所以不能围成腰长是4cm的等腰三角形. 由以上可知,可以围成底边是4cm的等腰三角形.
1、下列长度的各组线段能否组成一个三角形
(1)15cm、10cm、7cm; (2)2cm、6cm、10cm
(3)3cm、9cm、6cm; (4)3cm、5cm、6cm
随堂检测
2、在△ABC中,已知a=4cm,b=6cm,则c的取值范围是 ,
解: (1) ∵ 10+7>15, ∴能组成三角形;
(2) ∵ 2+6<10, ∴不能组成三角形;
(3) ∵ 3+6=9, ∴不能组成三角形;
(4) ∵ 3+5>6, ∴能组成三角形.
2cm已知a、b、c是三角形的三条边,化简|a+b-c|+|b-c-a|.
解:因为a、b、c是三角形的三边
所以 a+b-c>0(两边之和大于第三边)
b-c-a <0(两边之差小于第三边)
所以|a+b-c|+|c-b-a|=a+b-c-b+c+a
=2a
拓展提高
边、顶点、角
三角形的边
三角形的分类
三角形的三边关系
按角分类
按边分类
三角形两边之和
大于第三边
三角形两边之差
小于第三边
课堂小结
课后作业
3.(1)已知等腰三角形的一边长为6,一边长为8,求它的周长.
(2)已知等腰三角形的一边长为3,一边长为7,求它的周长.
1.若等腰三角形的两边长分别为4和12,则它的周长为_______; 若等腰三角形的两边长分别是3和5,则它的周长为_______ 。
2.如果以5cm为等腰三角形的一边,另一边为9cm,则它的周长为____________。
28
11或13
19cm或23cm
解:(1)边长分别为6、6、8或6、8、8,所以周长为20或22.
(2)边长分别为3、7、7或3、3、7,但因为3、3、7不能构成三角形,所以周长为17.
谢谢聆听
人教版数学八年级上册
第11.1.1三角形的边
情境引入
情境引入
在上面图片中你发现了哪些图形呢?
三角形
生活中还有许多使用三角形的实例,你能举例吗?
互动新授
观察下列图形,看一下哪些是三角形?
互动新授
三角形的定义:
由不在同一条直线上的三条线段首尾顺次连结所组成的图形,叫做三角形。
特征:
(1)三条线段
(2)不在同一直线上
(3)首尾顺次连接
A
B
C
互动新授
三角形表示方法:
三角形的顶点:
三角形相邻两边的公共端点叫做三角形的顶点。
顶点是A,B,C的三角形记作△ABC,读作“三角形ABC”.
顶点
通常:顶点A所对的边BC用a表示,顶点B所对的边CA用b表示,顶点C所对的边AB用c表示.
三角形的线段:
分别用AB, BC, AC表示
a
b
c
三角形的角:
互动新授
三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
A
B
C
对角:
对边:
BC边的对角是∠A
∠C的对边是BA ,通常简记为c
表示:∠A ,∠B, ∠C
1.图中有几个三角形?如何用符号表示这些三角形?以点E为顶点的三角形有哪几个?以∠D为角的三角形有哪些?
A
C
E
小试牛刀
共有5个三角形,
分别为:△ABE,△ABC,△BCD, △BCE,△CED.
以点E为顶点的三角形有3个,
分别为:△EAB,△ECD,△EBC.
以点E∠D为角的三角形有2个,
分别为:△DEC,△DBC
D
B
有两条边相等的三角形叫做等腰三角形。
三边都相等的三角形叫做等边三角形。
腰
腰
底
顶角
底角
底角
A
B
C
A
B
C
互动新授
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
三边都不相等的三角形
三角形的分类
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三边都不相等的三角形
等腰三角形
等边三角形
总结归纳
合作探究
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?能证明你的结论吗?
A
C
B
路线1:从点B到点A,再从点A到点C,长度:BA+AC.
路线2:从点B直接到点C,长度:BC.
BA+AC 和BC 的大小关系如何?
理由:“两点之间,线段最短”
可得:BA+AC>BC.
从B到A呢?有几条线路可以选择?各条线路的长有什么关系?
小结归纳
A
C
B
AC+CB>AB
BA+AC>BC
CB+BA>CA
BA>BC-AC
AC>AB-CB
CB>CA-BA
三角形的三边关系:
1、三角形两边之和大于第三边;
2、三角形两边之差小于第三边.
例1:判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm,9cm,5cm (2) 6cm,7cm,13cm
(3)5cm,7cm,9cm
典例精析
解:(1)不能,因为3cm+5cm<9cm,不满足两边之和大于第三边.
(2)不能,因为6cm+7cm=13cm,不满足两边之和大于第三边.
(3)能,因为5cm+7cm>9cm,5cm+9cm>7cm,7cm+9cm>5cm,或9cm-5cm<7cm,9cm-7cm<5cm,7cm-5cm<9cm.
有没有更简便的方法呢?
归纳:判断三条线段是否可以构成三角形,只需判断“两条较短的线段之和大于第三条”即可.
典例精析
例2:用一条长18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
解:(1)设底边长为xcm,则腰长为2xcm.
由题可得: x+2x+2x=18,
解得x=3.6.
所以,三边长分别为3.6cm,7.2cm,7.2cm.
例2:用一条长18cm的细绳围成一个等腰三角形.
(2)能围成有一边的长是4cm的等腰三角形吗?为什么?
典例精析
(2)因为长为4cm的边可能是腰,也可能是底边,所以要分情况讨论.
第一种情况:如果4cm的边为底边,设腰长为xcm,则,4+x+x=18,
解得:x=7.
第二种情况:如果4cm的边为腰长,设底边长为xcm,则,4+4+x=18,
解得:x=10.
因为4+4<10,不符合三角形两边的和大于第三边,所以不能围成腰长是4cm的等腰三角形. 由以上可知,可以围成底边是4cm的等腰三角形.
1、下列长度的各组线段能否组成一个三角形
(1)15cm、10cm、7cm; (2)2cm、6cm、10cm
(3)3cm、9cm、6cm; (4)3cm、5cm、6cm
随堂检测
2、在△ABC中,已知a=4cm,b=6cm,则c的取值范围是 ,
解: (1) ∵ 10+7>15, ∴能组成三角形;
(2) ∵ 2+6<10, ∴不能组成三角形;
(3) ∵ 3+6=9, ∴不能组成三角形;
(4) ∵ 3+5>6, ∴能组成三角形.
2cm
解:因为a、b、c是三角形的三边
所以 a+b-c>0(两边之和大于第三边)
b-c-a <0(两边之差小于第三边)
所以|a+b-c|+|c-b-a|=a+b-c-b+c+a
=2a
拓展提高
边、顶点、角
三角形的边
三角形的分类
三角形的三边关系
按角分类
按边分类
三角形两边之和
大于第三边
三角形两边之差
小于第三边
课堂小结
课后作业
3.(1)已知等腰三角形的一边长为6,一边长为8,求它的周长.
(2)已知等腰三角形的一边长为3,一边长为7,求它的周长.
1.若等腰三角形的两边长分别为4和12,则它的周长为_______; 若等腰三角形的两边长分别是3和5,则它的周长为_______ 。
2.如果以5cm为等腰三角形的一边,另一边为9cm,则它的周长为____________。
28
11或13
19cm或23cm
解:(1)边长分别为6、6、8或6、8、8,所以周长为20或22.
(2)边长分别为3、7、7或3、3、7,但因为3、3、7不能构成三角形,所以周长为17.
谢谢聆听
