专项训练:天体运动中的三类典型问题 -2022-2023学年高一下学期物理鲁科版(2019)必修第二册(word版含答案)
文档属性
| 名称 | 专项训练:天体运动中的三类典型问题 -2022-2023学年高一下学期物理鲁科版(2019)必修第二册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 766.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-09-03 11:41:32 | ||
图片预览



文档简介
专项训练:天体运动中的三类典型问题
一、基础巩固
1.由于通信和广播等方面的需要,许多国家发射了地球同步卫星,这些卫星的( )
A.质量可以不同
B.轨道半径可以不同
C.轨道平面可以不同
D.速率可以不同
2.如图所示,宇宙飞船A在低轨道上飞行,为了给更高轨道的空间站B输送物资,它可以采用喷气的方法改变速度,从而达到改变轨道的目的,则以下说法正确的是( )
A.它应沿运行速度方向喷气,与B对接后运行周期变小
B.它应沿运行速度的反方向喷气,与B对接后运行周期变大
C.它应沿运行速度方向喷气,与B对接后运行周期变大
D.它应沿运行速度的反方向喷气,与B对接后运行周期变小
3.(2022湖北武汉高一联考)2021年6月17日,神舟十二号载人飞船与天和核心舱成功对接,对接过程如图所示,天和核心舱处于半径为r3的圆轨道Ⅲ;神舟十二号载人飞船处于半径为r1的圆轨道Ⅰ,运行周期为T1,当经过A点时,通过变轨操作后,沿椭圆轨道Ⅱ运动到B处与天和核心舱对接,则神舟十二号载人飞船( )
A.沿轨道Ⅰ运行的周期大于天和核心舱沿轨道Ⅲ运行的周期
B.沿轨道Ⅱ从A运动到B的过程中,速度不断增大
C.在轨道Ⅰ上的速度小于沿轨道Ⅱ运动经过B点的速度
D.沿轨道Ⅱ运动经过B点的加速度与沿轨道Ⅲ运动经过B点的加速度相等
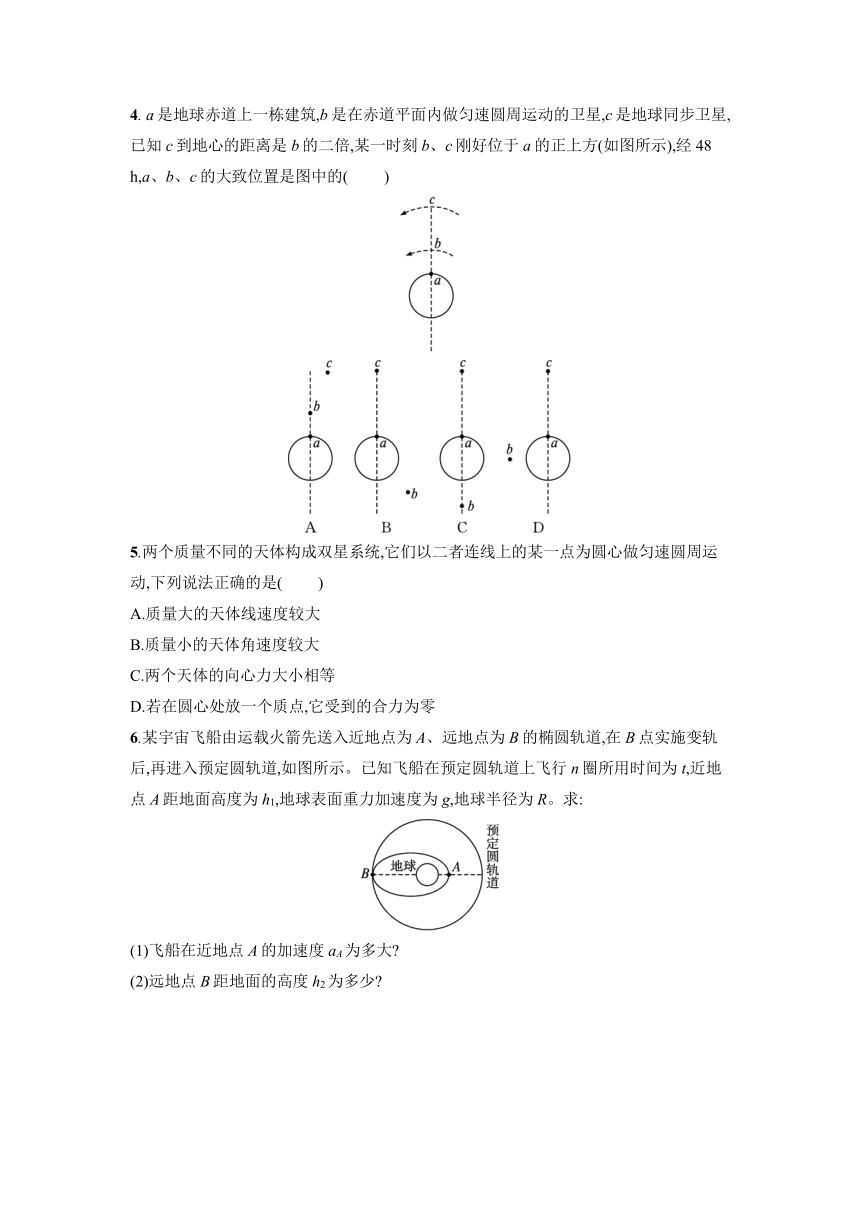
4. a是地球赤道上一栋建筑,b是在赤道平面内做匀速圆周运动的卫星,c是地球同步卫星,已知c到地心的距离是b的二倍,某一时刻b、c刚好位于a的正上方(如图所示),经48 h,a、b、c的大致位置是图中的( )
5.两个质量不同的天体构成双星系统,它们以二者连线上的某一点为圆心做匀速圆周运动,下列说法正确的是( )
A.质量大的天体线速度较大
B.质量小的天体角速度较大
C.两个天体的向心力大小相等
D.若在圆心处放一个质点,它受到的合力为零
6.某宇宙飞船由运载火箭先送入近地点为A、远地点为B的椭圆轨道,在B点实施变轨后,再进入预定圆轨道,如图所示。已知飞船在预定圆轨道上飞行n圈所用时间为t,近地点A距地面高度为h1,地球表面重力加速度为g,地球半径为R。求:
(1)飞船在近地点A的加速度aA为多大
(2)远地点B距地面的高度h2为多少
7.如图所示,两个星球A、B组成双星系统,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。已知A、B星球质量分别为mA、mB,引力常量为G,求(其中L为两星中心距离,T为两星的运动周期)。
二、能力提升
8.有a、b、c、d四颗地球卫星,a在地球赤道上未发射,b在地面附近近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星。各卫星排列位置如图,则有( )
A.a的向心加速度等于重力加速度g
B.b在相同时间内转过的弧长最长
C.c在4 h内转过的圆心角是
D.d的运行周期有可能是20 h
9.(多选)如图所示,甲、乙、丙是位于同一直线上的离其他恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行,若三颗星质量均为M,引力常量为G,则( )
A.甲星所受合外力为
B.乙星所受合外力为
C.甲星和丙星的线速度相同
D.甲星和丙星的角速度相同
10.(多选)经过科学家的努力,人类直接探测到了来自双中子星合并的引力波。根据科学家们复原的过程,在两颗中子星合并前约100 s时,它们相距约400 km,绕二者连线上的某点每秒转动12圈。将两颗中子星都看作是质量均匀分布的球体,由这些数据、引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星( )
A.质量之积 B.质量之和
C.速率之和 D.各自的自转角速度
11.“祝融号”火星车登陆火星之前,“天问一号”探测器沿椭圆形的停泊轨道绕火星飞行,其周期为2个火星日。假设某飞船沿圆轨道绕火星飞行,其周期也为2个火星日。已知一个火星日的时长约为一个地球日,火星质量约为地球质量的0.1,则该飞船的轨道半径与地球同步卫星的轨道半径的比值约为 。
12.宇宙间存在一些离其他恒星较远的三星系统。其中有一种三星系统如图所示,三颗质量均为m的星体位于等边三角形的三个顶点,三角形边长为R。忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心O做匀速圆周运动,引力常量为G。则每颗星做圆周运动的周期为多大
13.太阳系以外存在着许多恒星与行星组成的双星系统,它们运行的原理可以理解为,质量为m0的恒星和质量为m的行星(m0>m),在它们之间的万有引力作用下有规律地运动着。如图所示,我们可认为行星在以某一定点C为中心、半径为a的圆周上做匀速圆周运动(图中没有表示出恒星)。设引力常量为G,恒星和行星的大小可忽略不计。
(1)试在图中粗略画出恒星运动的轨道。
(2)试计算恒星与点C间的距离和恒星的运行速率v。
参考答案
一、基础巩固
1.答案:A
解析:地球同步卫星轨道必须在赤道平面内,离地面高度相同的同一轨道上,角速度、线速度、周期一定,与卫星的质量无关。选项A正确,B、C、D错误。
2.答案:B
解析:飞船由低轨道向高轨道运行时,需要提高在轨道上的运行速度,增加轨道高度才能使宇宙飞船A到达更高轨道与空间站B对接;由G=mr可知,r增大,T变大,选项B正确。
3.答案:D
解析:万有引力提供向心力G=mr,得T=,因为r14.答案:B
解析:在某时刻c在a的正上方,则以后永远在a的正上方,对b和c,根据G=mr,推知Tc=2Tb,又由2Tc=nbTb,得b卫星运行的圈数为nb=2×2=5.66,所以B正确。
5.答案:C
解析:双星系统的结构是稳定的,故它们的角速度相等,故B错误;两个星球间的万有引力提供向心力,根据牛顿第三定律可知,两个天体的向心力大小相等,故C正确;根据牛顿第二定律,有
G=m1ω2r1=m2ω2r2
其中r1+r2=L
故r1=L
r2=L
故
故质量大的天体线速度较小,A错误;
若在圆心处放一个质点,合力
F=G-G)≠0,故D错误。
6.答案:(1) (2)-R
解析:(1)设地球质量为M,飞船的质量为m,在A点飞船受到的地球引力为F=G,地球表面的重力加速度g=G
由牛顿第二定律得aA=。
(2)飞船在预定圆轨道飞行的周期T=
由牛顿第二定律得G=m2(R+h2)
解得h2=-R。
7.答案:
解析:设A、B两个星球做圆周运动的半径分别为rA、rB。则rA+rB=L,对星球A有G=mArA,对星球B有G=mBrB,联立以上三式求得。
二、能力提升
8.答案:B
解析:对于卫星a,根据万有引力定律、牛顿第二定律列式可得G-N=ma向,又由G=mg,故卫星a的向心加速度小于重力加速度g,选项A错误;由G=m得,v=,故轨道半径越小,线速度越大,故b、c、d三颗卫星的线速度的大小关系为vb>vc>vd,而卫星a与同步卫星c的周期相同,故卫星c的线速度大于卫星a的线速度,选项B正确;由c是地球同步卫星,可知卫星c在4 h内转过的圆心角是,选项C错误;由G=m2r得,T=2π,轨道半径越大,周期越长,故卫星d的周期大于同步卫星c的周期,选项D错误。
9.答案:AD
解析:由万有引力定律可知,甲、乙和乙、丙之间的万有引力大小均为F1=G,甲、丙之间的万有引力为F2=G,甲星所受两个引力的方向相同,故合力为F1+F2=,选项A正确;乙星所受两个引力等大、反向,合力为零,选项B错误;甲、丙两星线速度方向始终不同,选项C错误;由题知甲、丙两星周期相同,由角速度定义可知,甲、丙两星角速度相同,选项D正确。
10.答案:BC
解析:设两中子星质量为m1、m2,环绕半径为r1、r2,两星间距为r。所以有G=m1ω2r1,G=m2ω2r2
可解得m1=,m2=
所以m1+m2=,故B项正确;
设两星速率分别为v1、v2,所以有
v1+v2=ω(r1+r2)=ωr
由题意可得ω、r,故C项正确。
11.答案:
解析:设火星质量为M火,飞船的轨道半径为r1,周期为T1,地球质量为M,地球同步卫星的轨道半径为r,周期为T,对飞船有=mr1
对地球同步卫星有=m2r
联立解得。
12.答案:均为2π
解析:任意两个星体之间的万有引力F=,每一颗星体受到的合力F1=F
由几何关系知,它们的轨道半径r=R
合力提供它们的向心力
解得T=2π。
13.答案:(1)见解析
(2)a
解析:(1)恒星运动的轨道大致如图。
(2)对行星有F=mω2Rm
对恒星有F'=m0ω2Rm0
根据牛顿第三定律,F与F'大小相等
联立解得Rm0=a
对恒星有=G
代入数据得v=。
一、基础巩固
1.由于通信和广播等方面的需要,许多国家发射了地球同步卫星,这些卫星的( )
A.质量可以不同
B.轨道半径可以不同
C.轨道平面可以不同
D.速率可以不同
2.如图所示,宇宙飞船A在低轨道上飞行,为了给更高轨道的空间站B输送物资,它可以采用喷气的方法改变速度,从而达到改变轨道的目的,则以下说法正确的是( )
A.它应沿运行速度方向喷气,与B对接后运行周期变小
B.它应沿运行速度的反方向喷气,与B对接后运行周期变大
C.它应沿运行速度方向喷气,与B对接后运行周期变大
D.它应沿运行速度的反方向喷气,与B对接后运行周期变小
3.(2022湖北武汉高一联考)2021年6月17日,神舟十二号载人飞船与天和核心舱成功对接,对接过程如图所示,天和核心舱处于半径为r3的圆轨道Ⅲ;神舟十二号载人飞船处于半径为r1的圆轨道Ⅰ,运行周期为T1,当经过A点时,通过变轨操作后,沿椭圆轨道Ⅱ运动到B处与天和核心舱对接,则神舟十二号载人飞船( )
A.沿轨道Ⅰ运行的周期大于天和核心舱沿轨道Ⅲ运行的周期
B.沿轨道Ⅱ从A运动到B的过程中,速度不断增大
C.在轨道Ⅰ上的速度小于沿轨道Ⅱ运动经过B点的速度
D.沿轨道Ⅱ运动经过B点的加速度与沿轨道Ⅲ运动经过B点的加速度相等
4. a是地球赤道上一栋建筑,b是在赤道平面内做匀速圆周运动的卫星,c是地球同步卫星,已知c到地心的距离是b的二倍,某一时刻b、c刚好位于a的正上方(如图所示),经48 h,a、b、c的大致位置是图中的( )
5.两个质量不同的天体构成双星系统,它们以二者连线上的某一点为圆心做匀速圆周运动,下列说法正确的是( )
A.质量大的天体线速度较大
B.质量小的天体角速度较大
C.两个天体的向心力大小相等
D.若在圆心处放一个质点,它受到的合力为零
6.某宇宙飞船由运载火箭先送入近地点为A、远地点为B的椭圆轨道,在B点实施变轨后,再进入预定圆轨道,如图所示。已知飞船在预定圆轨道上飞行n圈所用时间为t,近地点A距地面高度为h1,地球表面重力加速度为g,地球半径为R。求:
(1)飞船在近地点A的加速度aA为多大
(2)远地点B距地面的高度h2为多少
7.如图所示,两个星球A、B组成双星系统,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。已知A、B星球质量分别为mA、mB,引力常量为G,求(其中L为两星中心距离,T为两星的运动周期)。
二、能力提升
8.有a、b、c、d四颗地球卫星,a在地球赤道上未发射,b在地面附近近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星。各卫星排列位置如图,则有( )
A.a的向心加速度等于重力加速度g
B.b在相同时间内转过的弧长最长
C.c在4 h内转过的圆心角是
D.d的运行周期有可能是20 h
9.(多选)如图所示,甲、乙、丙是位于同一直线上的离其他恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行,若三颗星质量均为M,引力常量为G,则( )
A.甲星所受合外力为
B.乙星所受合外力为
C.甲星和丙星的线速度相同
D.甲星和丙星的角速度相同
10.(多选)经过科学家的努力,人类直接探测到了来自双中子星合并的引力波。根据科学家们复原的过程,在两颗中子星合并前约100 s时,它们相距约400 km,绕二者连线上的某点每秒转动12圈。将两颗中子星都看作是质量均匀分布的球体,由这些数据、引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星( )
A.质量之积 B.质量之和
C.速率之和 D.各自的自转角速度
11.“祝融号”火星车登陆火星之前,“天问一号”探测器沿椭圆形的停泊轨道绕火星飞行,其周期为2个火星日。假设某飞船沿圆轨道绕火星飞行,其周期也为2个火星日。已知一个火星日的时长约为一个地球日,火星质量约为地球质量的0.1,则该飞船的轨道半径与地球同步卫星的轨道半径的比值约为 。
12.宇宙间存在一些离其他恒星较远的三星系统。其中有一种三星系统如图所示,三颗质量均为m的星体位于等边三角形的三个顶点,三角形边长为R。忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心O做匀速圆周运动,引力常量为G。则每颗星做圆周运动的周期为多大
13.太阳系以外存在着许多恒星与行星组成的双星系统,它们运行的原理可以理解为,质量为m0的恒星和质量为m的行星(m0>m),在它们之间的万有引力作用下有规律地运动着。如图所示,我们可认为行星在以某一定点C为中心、半径为a的圆周上做匀速圆周运动(图中没有表示出恒星)。设引力常量为G,恒星和行星的大小可忽略不计。
(1)试在图中粗略画出恒星运动的轨道。
(2)试计算恒星与点C间的距离和恒星的运行速率v。
参考答案
一、基础巩固
1.答案:A
解析:地球同步卫星轨道必须在赤道平面内,离地面高度相同的同一轨道上,角速度、线速度、周期一定,与卫星的质量无关。选项A正确,B、C、D错误。
2.答案:B
解析:飞船由低轨道向高轨道运行时,需要提高在轨道上的运行速度,增加轨道高度才能使宇宙飞船A到达更高轨道与空间站B对接;由G=mr可知,r增大,T变大,选项B正确。
3.答案:D
解析:万有引力提供向心力G=mr,得T=,因为r1
解析:在某时刻c在a的正上方,则以后永远在a的正上方,对b和c,根据G=mr,推知Tc=2Tb,又由2Tc=nbTb,得b卫星运行的圈数为nb=2×2=5.66,所以B正确。
5.答案:C
解析:双星系统的结构是稳定的,故它们的角速度相等,故B错误;两个星球间的万有引力提供向心力,根据牛顿第三定律可知,两个天体的向心力大小相等,故C正确;根据牛顿第二定律,有
G=m1ω2r1=m2ω2r2
其中r1+r2=L
故r1=L
r2=L
故
故质量大的天体线速度较小,A错误;
若在圆心处放一个质点,合力
F=G-G)≠0,故D错误。
6.答案:(1) (2)-R
解析:(1)设地球质量为M,飞船的质量为m,在A点飞船受到的地球引力为F=G,地球表面的重力加速度g=G
由牛顿第二定律得aA=。
(2)飞船在预定圆轨道飞行的周期T=
由牛顿第二定律得G=m2(R+h2)
解得h2=-R。
7.答案:
解析:设A、B两个星球做圆周运动的半径分别为rA、rB。则rA+rB=L,对星球A有G=mArA,对星球B有G=mBrB,联立以上三式求得。
二、能力提升
8.答案:B
解析:对于卫星a,根据万有引力定律、牛顿第二定律列式可得G-N=ma向,又由G=mg,故卫星a的向心加速度小于重力加速度g,选项A错误;由G=m得,v=,故轨道半径越小,线速度越大,故b、c、d三颗卫星的线速度的大小关系为vb>vc>vd,而卫星a与同步卫星c的周期相同,故卫星c的线速度大于卫星a的线速度,选项B正确;由c是地球同步卫星,可知卫星c在4 h内转过的圆心角是,选项C错误;由G=m2r得,T=2π,轨道半径越大,周期越长,故卫星d的周期大于同步卫星c的周期,选项D错误。
9.答案:AD
解析:由万有引力定律可知,甲、乙和乙、丙之间的万有引力大小均为F1=G,甲、丙之间的万有引力为F2=G,甲星所受两个引力的方向相同,故合力为F1+F2=,选项A正确;乙星所受两个引力等大、反向,合力为零,选项B错误;甲、丙两星线速度方向始终不同,选项C错误;由题知甲、丙两星周期相同,由角速度定义可知,甲、丙两星角速度相同,选项D正确。
10.答案:BC
解析:设两中子星质量为m1、m2,环绕半径为r1、r2,两星间距为r。所以有G=m1ω2r1,G=m2ω2r2
可解得m1=,m2=
所以m1+m2=,故B项正确;
设两星速率分别为v1、v2,所以有
v1+v2=ω(r1+r2)=ωr
由题意可得ω、r,故C项正确。
11.答案:
解析:设火星质量为M火,飞船的轨道半径为r1,周期为T1,地球质量为M,地球同步卫星的轨道半径为r,周期为T,对飞船有=mr1
对地球同步卫星有=m2r
联立解得。
12.答案:均为2π
解析:任意两个星体之间的万有引力F=,每一颗星体受到的合力F1=F
由几何关系知,它们的轨道半径r=R
合力提供它们的向心力
解得T=2π。
13.答案:(1)见解析
(2)a
解析:(1)恒星运动的轨道大致如图。
(2)对行星有F=mω2Rm
对恒星有F'=m0ω2Rm0
根据牛顿第三定律,F与F'大小相等
联立解得Rm0=a
对恒星有=G
代入数据得v=。
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
