北师大版九年级上册2.3.2用公式法解一元二次方程课件(共19张PPT)
文档属性
| 名称 | 北师大版九年级上册2.3.2用公式法解一元二次方程课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 556.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 19:31:01 | ||
图片预览





文档简介
(共19张PPT)
2.3.2 用公式法解一元二次方程(二)
授课人:fb
第二章 一元二次方程
一元二次方程求根公式
一般地,对于一元二次方程ax2+bx+c=0(a≠0),
温故知新
x=
+
-
2a
-b
当b2-4ac≥0时,它的根是:
一元二次方程根的判别式
一元二次方程根的情况:
(1)当Δ>0时,
(2)当Δ=0时,
(3)当Δ<0时,
方程有两个相等的实数根;
方程有两个不相等的实数根;
方程没有实数根。
温故知新
Δ= b2-4ac
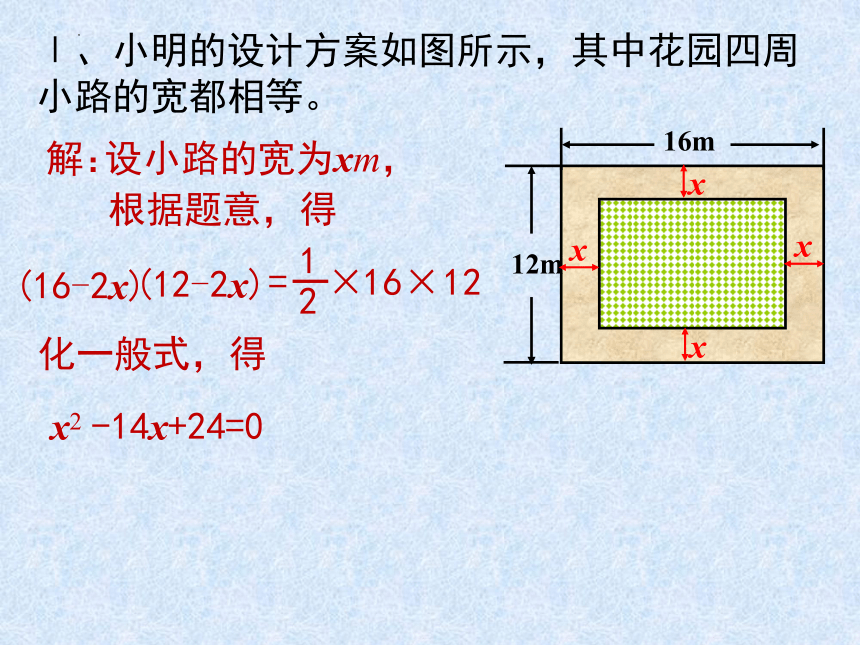
例1.在一块长16m、宽12m的矩形荒地上,要建造一个花园,并使花园所占面积为荒地面积的一半。你能给出设计方案吗?
16m
12m
新知探究
Ⅰ、小明的设计方案如图所示,其中花园四周小路的宽都相等。
解:
设小路的宽为xm,
化一般式,得
16m
12m
根据题意,得
(16-2x)
(12-2x)
16×12
2
1
=
×
x2 -14x+24=0
x
x
x
x
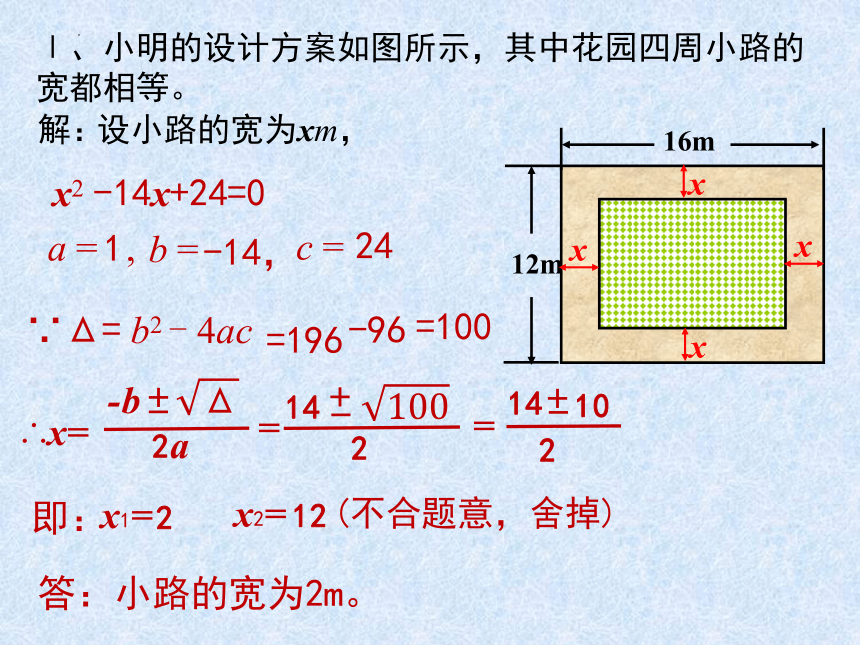
Ⅰ、小明的设计方案如图所示,其中花园四周小路的宽都相等。
解:
设小路的宽为xm,
答:小路的宽为2m。
16m
12m
x2 -14x+24=0
x
x
x
x
b =
-14,
a = ,
c =
1
∵Δ= b2 - 4ac
=196
-96
=100
+
-
∴x=
2a
-b
=
2
14
+
-
=
2
14
+
-
10
x1=
即:
x2=
2
12
(不合题意,舍掉)
24
温故知新
Ⅱ、小颖的设计方案如图所示,你能求出图中
的x吗?
16m
12m
xm
xm
解:
设小路的宽为xm,
化一般式,得
根据题意,得
16x
+12x
-x2
16×12
2
1
=
×
x2 -28x+96=0
16m
12m
xm
xm
解:
设小路的宽为xm,
(不合题意,舍去)
答:小路的宽为4m。
x2 -28x+96=0
b = ,
-28
96
a = ,
c =
1
∵Δ= b2 - 4ac
=784
-384
=400
∴x=
2a
-b
+
-
=
2
28
+
-
=
2
28
+
-
20
∴x1=
x2=
4
24
情境引入
Ⅲ、小亮的设计方案如图所示,其中花园每个角上的扇形都相同。
解:
设扇形半径为xm,
整理,得
根据题意,得
16m
12m
x
x=
πx2
16×12
2
1
=
×
x2 =
96
π
+
-
96
π
(不合题意,舍去)
∴x1≈
x2≈
5.5,
-5.5
答:扇形的半径约为5.5m。
其他方案
新知探究
例2、某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长25m),另三边用木栏围成。木栏长40m。鸡场的面积能达到180m吗?
设垂直于墙的木栏长为xm
根据题意:
化为一般形式:
x
(40-2x)
=180
x2 -20x+90=0
40-2x
25m
新知探究
解设垂直于墙的木栏长为xm
x2 -20x+90=0
40-2x
b = ,
-20
90
a = ,
c =
1
∵Δ= b2 - 4ac
=400
-360
=40
∴x=
2a
±
-b
=
2
20
±
=
2
20
±
=10
±
∴x1=
x2=
≈3.16
(舍去)
答:鸡场的面积能达到180m
25m
练一练
1.用一条长40cm的绳子围成一个面积为64cm2的长方形,设长方形的长为x cm,则可列方程为( )
A. x(20+x)=64 B. x(20-x)=64
C. x(40+x)=64 D. x(40-x)=64
B
练一练
2. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
B
(50+2x)
(80+2x)
=5400
练一练
3.如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为_____m.
2
(24-2x)
(30-3x)
=480
课堂小结
利用一元二次方程解决面积问题
几何图形
常见几何图形面积是等量关系
作业
P44-45
1,3,
例:解方程
2x2 - 4x –1 = 0.
这里 a = ,
∵ b2 - 4ac =
c = .
b = ,
解:
=24
(-4)2
>0,
×(-1)
-4×2
+
-
∴x=
2a
-b
=
4
4
+
-
=
4
4
+
-
2
-4
-1
x1=
即:
2
2+
x2=
2
2-
温故知新
(1)25x2 +20x +4 = 0.
a = ,
∵Δ= b2 - 4ac
c = .
b = ,
解(1)
=400
=202
×4
-4×25
25
20
4
温故知新
不解方程,判断下列方程的根的情况:
(2)5x2 +x =7
-400
=0
∴原方程有两个
相等的实数根。
解(2)
5x2 +x-7=0
a = ,
c = .
b = ,
5
1
-7
∵Δ= b2 - 4ac
=1
=12
×(-7)
-4×5
+141
>0
∴原方程有两个
不相等的实数根。
2.3.2 用公式法解一元二次方程(二)
授课人:fb
第二章 一元二次方程
一元二次方程求根公式
一般地,对于一元二次方程ax2+bx+c=0(a≠0),
温故知新
x=
+
-
2a
-b
当b2-4ac≥0时,它的根是:
一元二次方程根的判别式
一元二次方程根的情况:
(1)当Δ>0时,
(2)当Δ=0时,
(3)当Δ<0时,
方程有两个相等的实数根;
方程有两个不相等的实数根;
方程没有实数根。
温故知新
Δ= b2-4ac
例1.在一块长16m、宽12m的矩形荒地上,要建造一个花园,并使花园所占面积为荒地面积的一半。你能给出设计方案吗?
16m
12m
新知探究
Ⅰ、小明的设计方案如图所示,其中花园四周小路的宽都相等。
解:
设小路的宽为xm,
化一般式,得
16m
12m
根据题意,得
(16-2x)
(12-2x)
16×12
2
1
=
×
x2 -14x+24=0
x
x
x
x
Ⅰ、小明的设计方案如图所示,其中花园四周小路的宽都相等。
解:
设小路的宽为xm,
答:小路的宽为2m。
16m
12m
x2 -14x+24=0
x
x
x
x
b =
-14,
a = ,
c =
1
∵Δ= b2 - 4ac
=196
-96
=100
+
-
∴x=
2a
-b
=
2
14
+
-
=
2
14
+
-
10
x1=
即:
x2=
2
12
(不合题意,舍掉)
24
温故知新
Ⅱ、小颖的设计方案如图所示,你能求出图中
的x吗?
16m
12m
xm
xm
解:
设小路的宽为xm,
化一般式,得
根据题意,得
16x
+12x
-x2
16×12
2
1
=
×
x2 -28x+96=0
16m
12m
xm
xm
解:
设小路的宽为xm,
(不合题意,舍去)
答:小路的宽为4m。
x2 -28x+96=0
b = ,
-28
96
a = ,
c =
1
∵Δ= b2 - 4ac
=784
-384
=400
∴x=
2a
-b
+
-
=
2
28
+
-
=
2
28
+
-
20
∴x1=
x2=
4
24
情境引入
Ⅲ、小亮的设计方案如图所示,其中花园每个角上的扇形都相同。
解:
设扇形半径为xm,
整理,得
根据题意,得
16m
12m
x
x=
πx2
16×12
2
1
=
×
x2 =
96
π
+
-
96
π
(不合题意,舍去)
∴x1≈
x2≈
5.5,
-5.5
答:扇形的半径约为5.5m。
其他方案
新知探究
例2、某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长25m),另三边用木栏围成。木栏长40m。鸡场的面积能达到180m吗?
设垂直于墙的木栏长为xm
根据题意:
化为一般形式:
x
(40-2x)
=180
x2 -20x+90=0
40-2x
25m
新知探究
解设垂直于墙的木栏长为xm
x2 -20x+90=0
40-2x
b = ,
-20
90
a = ,
c =
1
∵Δ= b2 - 4ac
=400
-360
=40
∴x=
2a
±
-b
=
2
20
±
=
2
20
±
=10
±
∴x1=
x2=
≈3.16
(舍去)
答:鸡场的面积能达到180m
25m
练一练
1.用一条长40cm的绳子围成一个面积为64cm2的长方形,设长方形的长为x cm,则可列方程为( )
A. x(20+x)=64 B. x(20-x)=64
C. x(40+x)=64 D. x(40-x)=64
B
练一练
2. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
B
(50+2x)
(80+2x)
=5400
练一练
3.如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为_____m.
2
(24-2x)
(30-3x)
=480
课堂小结
利用一元二次方程解决面积问题
几何图形
常见几何图形面积是等量关系
作业
P44-45
1,3,
例:解方程
2x2 - 4x –1 = 0.
这里 a = ,
∵ b2 - 4ac =
c = .
b = ,
解:
=24
(-4)2
>0,
×(-1)
-4×2
+
-
∴x=
2a
-b
=
4
4
+
-
=
4
4
+
-
2
-4
-1
x1=
即:
2
2+
x2=
2
2-
温故知新
(1)25x2 +20x +4 = 0.
a = ,
∵Δ= b2 - 4ac
c = .
b = ,
解(1)
=400
=202
×4
-4×25
25
20
4
温故知新
不解方程,判断下列方程的根的情况:
(2)5x2 +x =7
-400
=0
∴原方程有两个
相等的实数根。
解(2)
5x2 +x-7=0
a = ,
c = .
b = ,
5
1
-7
∵Δ= b2 - 4ac
=1
=12
×(-7)
-4×5
+141
>0
∴原方程有两个
不相等的实数根。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
