1.2.2 数轴 课件(共40张PPT)
文档属性
| 名称 | 1.2.2 数轴 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1001.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 10:30:32 | ||
图片预览







文档简介
(共40张PPT)
1.2.2 数轴
第 1 章 有 理 数
七年级上册数学人教版
目录
数轴的概念及画法
01
在数轴上表示有理
数
0
2
知识回顾
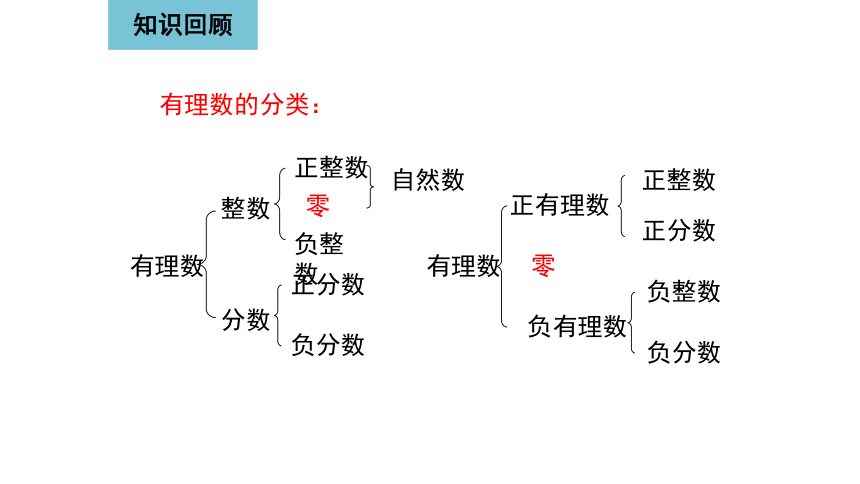
有理数
正整数
正分数
负分数
整数
分数
零
负整数
自然数
有理数的分类:
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
学习目标
1.掌握数轴的概念,理解数轴上的点和有理数的对应关系.
2.会正确的画出数轴,利用数轴上的点表示有理数.
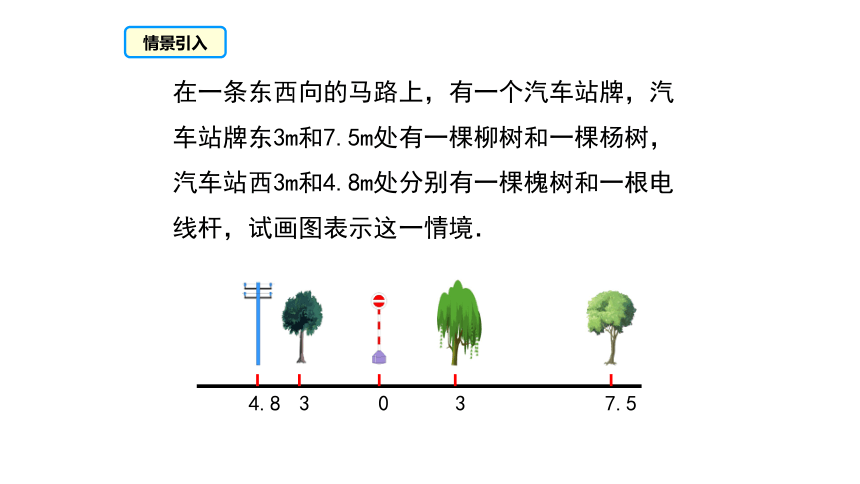
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
情景引入
B
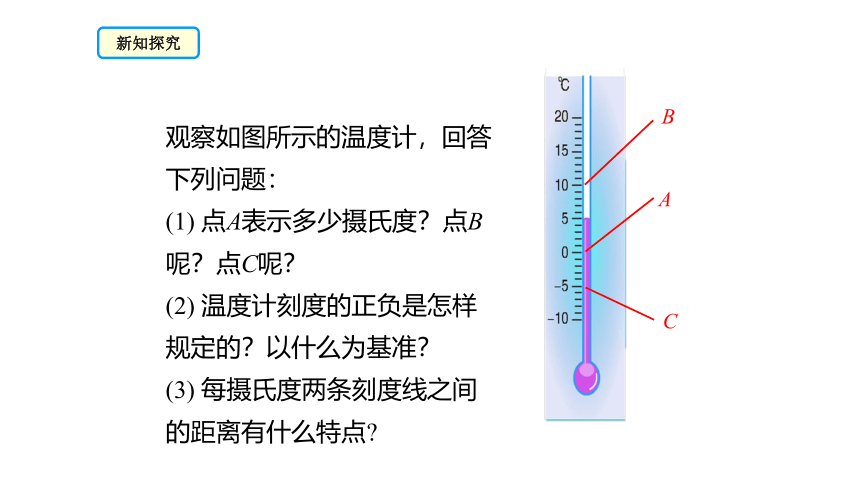
观察如图所示的温度计,回答下列问题:
(1) 点A表示多少摄氏度?点B呢?点C呢?
(2) 温度计刻度的正负是怎样规定的?以什么为基准?
(3) 每摄氏度两条刻度线之间的距离有什么特点
A
C
新知探究
0
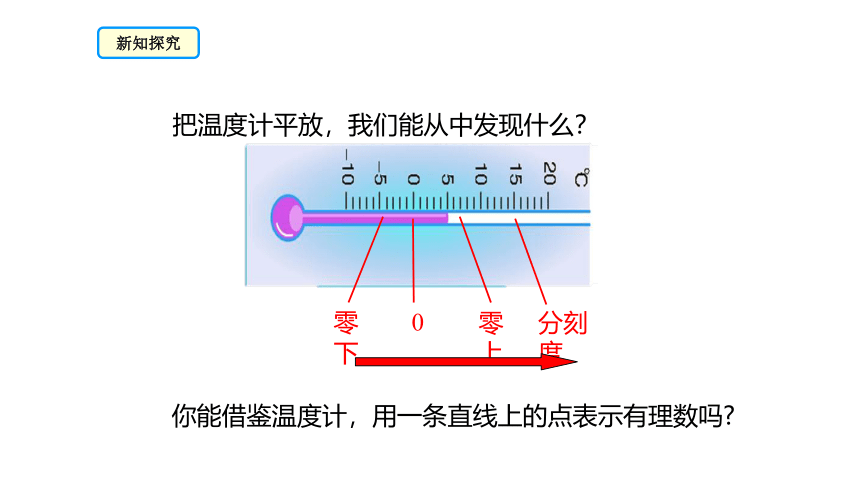
把温度计平放,我们能从中发现什么?
零下
零上
分刻度
你能借鉴温度计,用一条直线上的点表示有理数吗
新知探究
1.数轴的概念及画法
0
-3 -2 -1 1 2 3
1.什么是数轴?
原点
正方向
单位长度
规定了原点、正方向、单位长度的直线叫做数轴.
2.注意事项:
(1)数轴是一条特殊的直线;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度.
数轴的概念及画法
一
0
-3 -2 -1 1 2 3
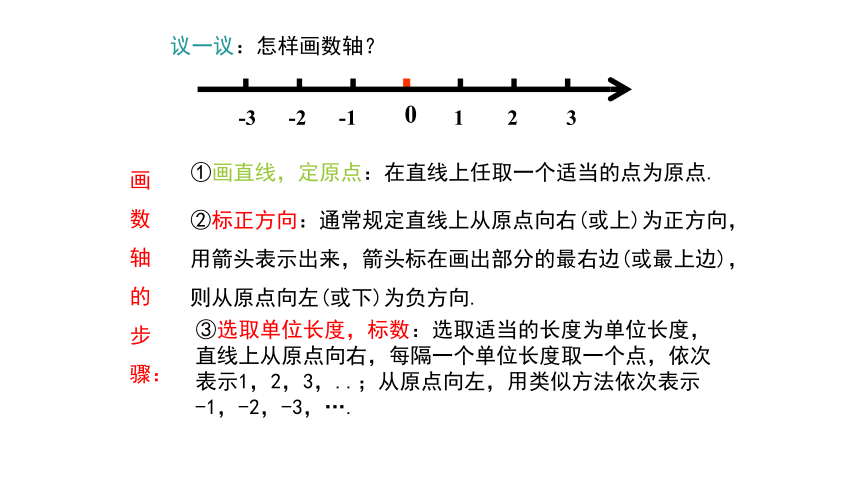
议一议:怎样画数轴?
①画直线,定原点:在直线上任取一个适当的点为原点.
②标正方向:通常规定直线上从原点向右(或上)为正方向,用箭头表示出来,箭头标在画出部分的最右边(或最上边),则从原点向左(或下)为负方向.
③选取单位长度,标数:选取适当的长度为单位长度,
直线上从原点向右,每隔一个单位长度取一个点,依次
表示1,2,3,..;从原点向左,用类似方法依次表示
-1,-2,-3,….
画
数
轴
的
步
骤:
(1) 原点、单位长度和正方向三要素缺一不可;
(2) 直线一般画水平的;
(3) 正方向用箭头表示,一般取从左到右;
(4) 取单位长度应结合实际需要,但要做到刻度均匀.
画数轴注意事项:
观察下列图形,指出哪条数轴画得正确,其余错在哪里?
1
2
3
A
0
1
-1
2
B
1
0
1
-1
-2
2
E
-1
0
D
-2
-2
0
2
-4
-6
4
C
6
说一说
例1 .关于数轴,下列说法最准确的是( )
A.一条直线
B.有原点、正方向的一条直线
C.有单位长度的一条直线
D.规定了原点、正方向、单位长度的直线
D
典例精析
下列图中所画数轴正确的是( )
D
典例精练
2.在数轴上表示有理数
0
-3 -2 -1 1 2 3
思考:
3.如何用数轴上的点来表示分数或小数?
如:1.5,- — 怎样表示.
2
3
.
.
在数轴上表示有理数
二
1.观察上面数轴,哪些数在原点的左边,哪些数在原点的右边,由此你有什么发现?
2.每个数到原点的距离是多少?由此你又有什么发现?
例2 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, ,0
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:如图所示
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看.
4
典例精析
任何一个有理数都可以用数轴上的一个点来表示.
一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
归纳
右
a
a
左
用数轴上的点表示有理数时,(1)正数用数轴上原点
右边的点表示;(2)负数用数轴上原点左边的点表示;(3)0用数轴
的原点表示.
0
1 2
-2 -1
例3 在下面数轴上,A,B,C,D各点分别表示什么数?
D C B A
D点表示-1.5
A点表示2;
B点表示0.25;
C点表示-0.75;
解:
.
.
.
.
1.如图,在数轴上点A表示的数可能是( )
A.-2.6 B.-2.4
C.-3.6 D.-3.4
B
典例精练
2.在数轴上表示-2的点是( )
A.点A B.点B
C.点C D.点D
A
3. a,b,c在数轴上的位置如图,则( )
A.a,b,c均是正数
B.a,b,c均是负数
C.a,b是正数,c是负数
D.a,b是负数,c是正数
D
C
右
4
左
4
2
4
-4
6.如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是____.
2
7.指出数轴上点A,B,C,D表示的数.
解:A点表示0,B点表示1.5,C点表示-2,D点表示3
(1)
(2)
(3)
(4)
1.下列各图是数轴吗?说明你的理由.
0
-3 -2 -1 1 2 3
-3 -2 -1 1 2 3 4
-3 -2 -1 1 2 3
0
0
×
×
×
×
当堂练习
2.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是
0,-2,1,2.5,-3.
教材9页练习1
3. 画出数轴并表示下列有理数:
1.5, -2, 2, -2.5, , ,0.
1.5
-2
2
-2.5
0
-5 -4 -3 -2 -1 0 1 2 3 4 5
﹒
﹒
﹒
﹒
﹒
﹒
﹒
教材9页练习2
4. 请写出数轴上点A、B、C、D、E所表示的数:
解:点A表示 ;点B表示 ;点C表示 ;点D表示 ;点E表示 .
0
-2
1
2.5
-3
5. 数轴上,如果表示数a的点在原点的左边,那么a是
一个______数;如果表示数b的点在原点的右边,那么b是一
个_____数.
负
正
教材9页练习1
教材9页练习4
6.在数轴上表示-1和2 019的两点分别为A和B,则A,B两点之间的距离为( )
A.2017 B.2018 C.2019 D.2020
D
7.如图,在数轴上,点A表示的数为-1,点B表示的数为4,若点C在点A的左侧,且A,C两点之间的距离等于A,B两点之间的距离,则点C表示的数为 .
-6
解:如图:
随堂检测
2.下列说法中正确的是( )
A.数轴上一个点可以表示两个不同的有理数
B.数轴上两个不同的点可以表示同一个有理数
C.有的有理数不能表示在数轴上,如-0.000 05
D.任何一个有理数都可在数轴上找到和它对应的唯一的一个点
D
3.在数轴上,一点从原点开始,先向右移动2个单位长度,再向左移动3个单位长度后到达终点,这个终点表示的数是( )
A.5 B.1 C.-1 D.-5
4.在数轴上到原点的距离等于2的点所表示的数是( )
A.-2 B.2
C.±2 D.不能确定
C
C
5.在数轴上,点A,点B分别表示-2,-1,任意写出一个在点A右边且在点B左边的点表示的数__________________________.
6.小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数共有____个.
-1.5(答案不唯一)
7
7.如图,点A表示的数是-4.
(1)在数轴上标出原点O;
(2)指出点B所表示的数;
(3)在数轴上找一点C,它与B点的距离为2个单位长度,那么C点表示什么数?
解:(1)原点O在点A的右侧4个单位长度处,如图:
(2)点B表示3 (3)C点表示1或5
8.小敏家、学校、邮局、图书馆坐落在一条东西走向的大街上,依次记为A,B,C,D,学校位于小敏家西150米,邮局位于小敏家东100米,图书馆位于小敏家西400米.
(1)用数轴表示A,B,C,D的位置;
(2)一天小敏从家里先去邮局寄信后,以每分钟50米的速度往图书馆方向走了约8分钟,试问这时小敏约在什么位置?距图书馆和学校各约多少米?
解:(1)
(2)小敏从邮局出发,以每分钟50米的速度往图书馆方向走了约8分钟,其路程为50×8=400(米),结合(1)中数轴知,C,D之间相距500米,B,C之间相距250米,此时小敏在学校与图书馆之间,距图书馆约100米,距学校约150米
9. (1)借助数轴,回答下列问题:
①从-1到1有3个整数,分别是_____________________;
②从-2到2有5个整数,分别是____________________________;
③从-3到3有7个整数,分别是_________________________________;
④从-100到100有______________________个整数;
⑤从-n到n有____________________个整数.
-1,0,1
-2,-1,0,1,2
-3,-2,-1,0,1,2,3
201
(2n+1)
(2)根据以上规律,直接写出从-3.9到3.9有____个整数,从-10.1到10.1有____个整数.
(3)在单位长度是1 cm的数轴上任意画一条长度为1 000 cm的线段AB,线段AB盖住的整数点最多有多少个?
解:1 001个
7
21
1.数轴的定义:规定了原点、正方向和单位长度的直线叫数轴.
2.数轴的画法.
3.所有的有理数都可以用数轴上的点来表示,原点右边的数是正数,原点左边的数是负数,0是正负数的分界限.
课堂小结
1.2.2 数轴
第 1 章 有 理 数
七年级上册数学人教版
目录
数轴的概念及画法
01
在数轴上表示有理
数
0
2
知识回顾
有理数
正整数
正分数
负分数
整数
分数
零
负整数
自然数
有理数的分类:
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
学习目标
1.掌握数轴的概念,理解数轴上的点和有理数的对应关系.
2.会正确的画出数轴,利用数轴上的点表示有理数.
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
情景引入
B
观察如图所示的温度计,回答下列问题:
(1) 点A表示多少摄氏度?点B呢?点C呢?
(2) 温度计刻度的正负是怎样规定的?以什么为基准?
(3) 每摄氏度两条刻度线之间的距离有什么特点
A
C
新知探究
0
把温度计平放,我们能从中发现什么?
零下
零上
分刻度
你能借鉴温度计,用一条直线上的点表示有理数吗
新知探究
1.数轴的概念及画法
0
-3 -2 -1 1 2 3
1.什么是数轴?
原点
正方向
单位长度
规定了原点、正方向、单位长度的直线叫做数轴.
2.注意事项:
(1)数轴是一条特殊的直线;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度.
数轴的概念及画法
一
0
-3 -2 -1 1 2 3
议一议:怎样画数轴?
①画直线,定原点:在直线上任取一个适当的点为原点.
②标正方向:通常规定直线上从原点向右(或上)为正方向,用箭头表示出来,箭头标在画出部分的最右边(或最上边),则从原点向左(或下)为负方向.
③选取单位长度,标数:选取适当的长度为单位长度,
直线上从原点向右,每隔一个单位长度取一个点,依次
表示1,2,3,..;从原点向左,用类似方法依次表示
-1,-2,-3,….
画
数
轴
的
步
骤:
(1) 原点、单位长度和正方向三要素缺一不可;
(2) 直线一般画水平的;
(3) 正方向用箭头表示,一般取从左到右;
(4) 取单位长度应结合实际需要,但要做到刻度均匀.
画数轴注意事项:
观察下列图形,指出哪条数轴画得正确,其余错在哪里?
1
2
3
A
0
1
-1
2
B
1
0
1
-1
-2
2
E
-1
0
D
-2
-2
0
2
-4
-6
4
C
6
说一说
例1 .关于数轴,下列说法最准确的是( )
A.一条直线
B.有原点、正方向的一条直线
C.有单位长度的一条直线
D.规定了原点、正方向、单位长度的直线
D
典例精析
下列图中所画数轴正确的是( )
D
典例精练
2.在数轴上表示有理数
0
-3 -2 -1 1 2 3
思考:
3.如何用数轴上的点来表示分数或小数?
如:1.5,- — 怎样表示.
2
3
.
.
在数轴上表示有理数
二
1.观察上面数轴,哪些数在原点的左边,哪些数在原点的右边,由此你有什么发现?
2.每个数到原点的距离是多少?由此你又有什么发现?
例2 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, ,0
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:如图所示
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看.
4
典例精析
任何一个有理数都可以用数轴上的一个点来表示.
一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
归纳
右
a
a
左
用数轴上的点表示有理数时,(1)正数用数轴上原点
右边的点表示;(2)负数用数轴上原点左边的点表示;(3)0用数轴
的原点表示.
0
1 2
-2 -1
例3 在下面数轴上,A,B,C,D各点分别表示什么数?
D C B A
D点表示-1.5
A点表示2;
B点表示0.25;
C点表示-0.75;
解:
.
.
.
.
1.如图,在数轴上点A表示的数可能是( )
A.-2.6 B.-2.4
C.-3.6 D.-3.4
B
典例精练
2.在数轴上表示-2的点是( )
A.点A B.点B
C.点C D.点D
A
3. a,b,c在数轴上的位置如图,则( )
A.a,b,c均是正数
B.a,b,c均是负数
C.a,b是正数,c是负数
D.a,b是负数,c是正数
D
C
右
4
左
4
2
4
-4
6.如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是____.
2
7.指出数轴上点A,B,C,D表示的数.
解:A点表示0,B点表示1.5,C点表示-2,D点表示3
(1)
(2)
(3)
(4)
1.下列各图是数轴吗?说明你的理由.
0
-3 -2 -1 1 2 3
-3 -2 -1 1 2 3 4
-3 -2 -1 1 2 3
0
0
×
×
×
×
当堂练习
2.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是
0,-2,1,2.5,-3.
教材9页练习1
3. 画出数轴并表示下列有理数:
1.5, -2, 2, -2.5, , ,0.
1.5
-2
2
-2.5
0
-5 -4 -3 -2 -1 0 1 2 3 4 5
﹒
﹒
﹒
﹒
﹒
﹒
﹒
教材9页练习2
4. 请写出数轴上点A、B、C、D、E所表示的数:
解:点A表示 ;点B表示 ;点C表示 ;点D表示 ;点E表示 .
0
-2
1
2.5
-3
5. 数轴上,如果表示数a的点在原点的左边,那么a是
一个______数;如果表示数b的点在原点的右边,那么b是一
个_____数.
负
正
教材9页练习1
教材9页练习4
6.在数轴上表示-1和2 019的两点分别为A和B,则A,B两点之间的距离为( )
A.2017 B.2018 C.2019 D.2020
D
7.如图,在数轴上,点A表示的数为-1,点B表示的数为4,若点C在点A的左侧,且A,C两点之间的距离等于A,B两点之间的距离,则点C表示的数为 .
-6
解:如图:
随堂检测
2.下列说法中正确的是( )
A.数轴上一个点可以表示两个不同的有理数
B.数轴上两个不同的点可以表示同一个有理数
C.有的有理数不能表示在数轴上,如-0.000 05
D.任何一个有理数都可在数轴上找到和它对应的唯一的一个点
D
3.在数轴上,一点从原点开始,先向右移动2个单位长度,再向左移动3个单位长度后到达终点,这个终点表示的数是( )
A.5 B.1 C.-1 D.-5
4.在数轴上到原点的距离等于2的点所表示的数是( )
A.-2 B.2
C.±2 D.不能确定
C
C
5.在数轴上,点A,点B分别表示-2,-1,任意写出一个在点A右边且在点B左边的点表示的数__________________________.
6.小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数共有____个.
-1.5(答案不唯一)
7
7.如图,点A表示的数是-4.
(1)在数轴上标出原点O;
(2)指出点B所表示的数;
(3)在数轴上找一点C,它与B点的距离为2个单位长度,那么C点表示什么数?
解:(1)原点O在点A的右侧4个单位长度处,如图:
(2)点B表示3 (3)C点表示1或5
8.小敏家、学校、邮局、图书馆坐落在一条东西走向的大街上,依次记为A,B,C,D,学校位于小敏家西150米,邮局位于小敏家东100米,图书馆位于小敏家西400米.
(1)用数轴表示A,B,C,D的位置;
(2)一天小敏从家里先去邮局寄信后,以每分钟50米的速度往图书馆方向走了约8分钟,试问这时小敏约在什么位置?距图书馆和学校各约多少米?
解:(1)
(2)小敏从邮局出发,以每分钟50米的速度往图书馆方向走了约8分钟,其路程为50×8=400(米),结合(1)中数轴知,C,D之间相距500米,B,C之间相距250米,此时小敏在学校与图书馆之间,距图书馆约100米,距学校约150米
9. (1)借助数轴,回答下列问题:
①从-1到1有3个整数,分别是_____________________;
②从-2到2有5个整数,分别是____________________________;
③从-3到3有7个整数,分别是_________________________________;
④从-100到100有______________________个整数;
⑤从-n到n有____________________个整数.
-1,0,1
-2,-1,0,1,2
-3,-2,-1,0,1,2,3
201
(2n+1)
(2)根据以上规律,直接写出从-3.9到3.9有____个整数,从-10.1到10.1有____个整数.
(3)在单位长度是1 cm的数轴上任意画一条长度为1 000 cm的线段AB,线段AB盖住的整数点最多有多少个?
解:1 001个
7
21
1.数轴的定义:规定了原点、正方向和单位长度的直线叫数轴.
2.数轴的画法.
3.所有的有理数都可以用数轴上的点来表示,原点右边的数是正数,原点左边的数是负数,0是正负数的分界限.
课堂小结
