1.2.4 绝对值(第1课时) 课件(共23张PPT)
文档属性
| 名称 | 1.2.4 绝对值(第1课时) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 708.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 10:44:31 | ||
图片预览







文档简介
(共23张PPT)
1.2.4 绝对值(第1课时)
第 1 章 有 理 数
七年级上册数学人教版
目录
绝对值的概念
01
绝对值的性质
02
2.掌握绝对值性质(难点)
1.理解绝对值的概念并能求一个数的绝对值.(重点)
学习目标
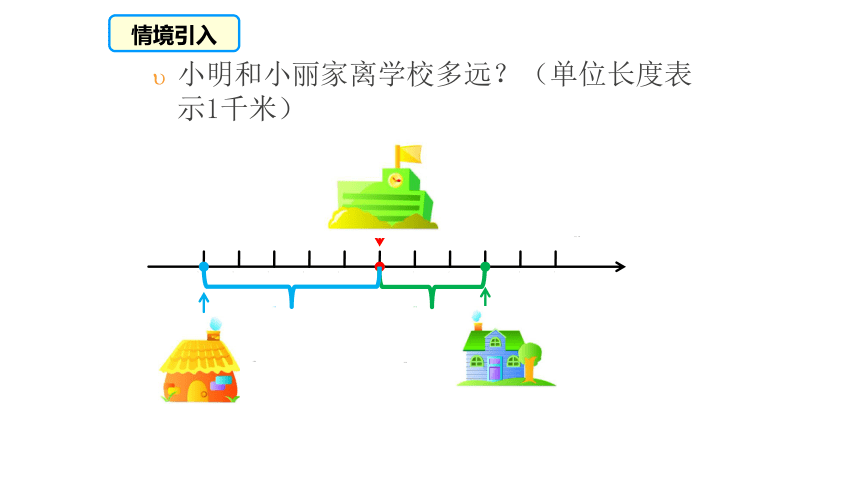
小明和小丽家离学校多远?(单位长度表示1千米)
0
1
2
3
4
5
-5
-4
-3
-2
-1
小明家
小丽家
单位:千米
3千米
5千米
情境引入
1.绝对值的概念
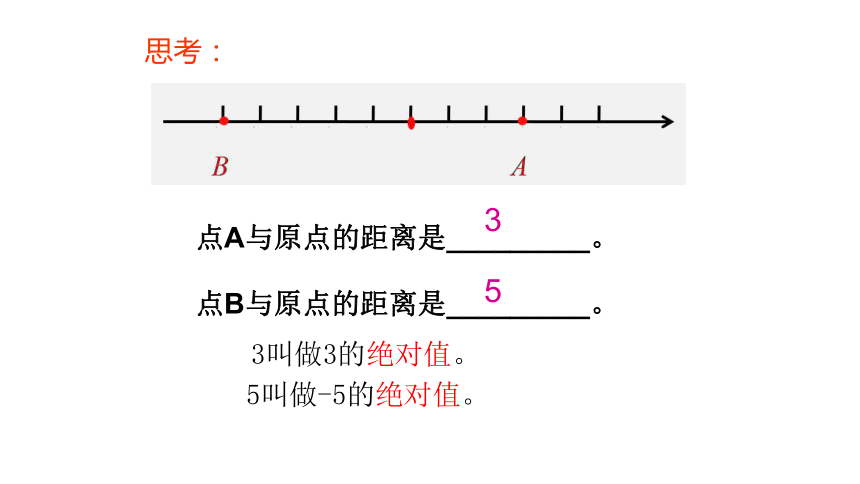
点A与原点的距离是_________。
点B与原点的距离是_________。
3
5
3叫做3的绝对值。
5叫做-5的绝对值。
思考:
绝对值的概念:
一个数在数轴上所对应的点与原点的距离,叫做这个数的绝对值。
绝对值一般用符号“| |”表示。
如:|a|表示数a的绝对值。
绝对值
一
填空:
|4|=4
4的绝对值是____,记作__________。
4
-3的绝对值是____,记作__________。
0的绝对值是____,记作__________。
3
0
|-3|=3
|0|=0
观察思考:
正数、负数、0的绝对值分别是什么?
2.绝对值的性质
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
零的绝对值是零。
绝对值的性质:
例1:
解:
典例精析
1.若|a|= 3 ,那么a =
2.若|-b|=7,那么b=
±3
±7
典例精练
3.在数轴上,到原点的距离等于3.5个单位长度的点所表示的有理数是____________。
4.__________的绝对值是它本身,________的绝对值是它的相反数。
+3.5, -3.5
正数和0
负数和0
(1)绝对值是6的数有___个,是_________;
(2)如果|x|=5,则x=________;
(3)绝对值最小的整数是______;
(4)写出绝对值小于3的整数_________;
(5) |-22.8|=_____,-|-7.5|=______
6和-6
5或-5
0
-2,-1,0,1,2
22.8
-7.5
当堂练习
B A 随堂检测B D 5.若a是有理数,则下面说法正确的是( )A.|a|一定是正数 B.|-a|一定是正数C.-|a|一定是正数 D.|a|一定是非负数6.已知|a|=0,则a=____.7.若a位于数轴上原点的左侧,且|a|=3.14,则a=_________.8.【四川攀枝花中考】|-3|的相反数是______.D 0 -3.14 -3 10.如果|x|=|-5|,那么x等于( )A.5 B.-5C.5或-5 D.以上都不对11.若a为有理数,且|a|=-a,那么a是( )A.正数 B.负数 C.非负数 D.非正数C D 12.【易错题】下列说法中,正确的是( )A.一个有理数的绝对值不小于它自身B.若两个有理数的绝对值相等,则这两个数相等C.若两个有理数的绝对值相等,则这两个数互为相反数D.-a的绝对值等于aA 解析:正数和0的绝对值是它本身,负数的绝对值是它的相反数,所以一个有理数的绝对值不小于它自身,A正确;若两个有理数的绝对值相等,则这两个数相等或互为相反数,B、C错误;当a<0时,-a的绝对值等于-a,D错误.13.化简:|π-4|+|3-π|=____.14.若|m-n+2|+|m-3|=0,求m+n的值.1 解:因为|m-n+2|≥0,|m-3|≥0,|m-n+2|+|m-3|=0,所以|m-n+2|=0,|m-3|=0,所以m=3,n=5,m+n=8.15.在各项国际乒乓球大赛中,国际乒联对乒乓球的直径有严格的规定.现有5个乒乓球,测量它们的直径,超过标准直径的毫米数记为正数,不足的记为负数.检测结果如下:A.+0.1毫米;B.-0.3毫米;C.+0.2毫米;D.-0.05毫米;E.-0.1毫米.你认为选哪一个乒乓球用于比赛最好呢?为什么?解:选乒乓球D用于比赛最好.理由:因为|+0.1|=0.1,|-0.3|=0.3,|+0.2|=0.2,|-0.05|=0.05,|-0.1|=0.1,0.05<0.1<0.2<0.3,所以乒乓球D的直径最接近于标准直径,选乒乓球D用于比赛最好.(2)当a是负数时,|a|=
2.(1)当a是正数时,|a|=
(3)当a=0时,|a|=
a
-a
0
课堂小结
数轴上表示数a的点与原点的距离叫做数a的绝对值。
3.互为相反数的两个数的绝对值相等
1.2.4 绝对值(第1课时)
第 1 章 有 理 数
七年级上册数学人教版
目录
绝对值的概念
01
绝对值的性质
02
2.掌握绝对值性质(难点)
1.理解绝对值的概念并能求一个数的绝对值.(重点)
学习目标
小明和小丽家离学校多远?(单位长度表示1千米)
0
1
2
3
4
5
-5
-4
-3
-2
-1
小明家
小丽家
单位:千米
3千米
5千米
情境引入
1.绝对值的概念
点A与原点的距离是_________。
点B与原点的距离是_________。
3
5
3叫做3的绝对值。
5叫做-5的绝对值。
思考:
绝对值的概念:
一个数在数轴上所对应的点与原点的距离,叫做这个数的绝对值。
绝对值一般用符号“| |”表示。
如:|a|表示数a的绝对值。
绝对值
一
填空:
|4|=4
4的绝对值是____,记作__________。
4
-3的绝对值是____,记作__________。
0的绝对值是____,记作__________。
3
0
|-3|=3
|0|=0
观察思考:
正数、负数、0的绝对值分别是什么?
2.绝对值的性质
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
零的绝对值是零。
绝对值的性质:
例1:
解:
典例精析
1.若|a|= 3 ,那么a =
2.若|-b|=7,那么b=
±3
±7
典例精练
3.在数轴上,到原点的距离等于3.5个单位长度的点所表示的有理数是____________。
4.__________的绝对值是它本身,________的绝对值是它的相反数。
+3.5, -3.5
正数和0
负数和0
(1)绝对值是6的数有___个,是_________;
(2)如果|x|=5,则x=________;
(3)绝对值最小的整数是______;
(4)写出绝对值小于3的整数_________;
(5) |-22.8|=_____,-|-7.5|=______
6和-6
5或-5
0
-2,-1,0,1,2
22.8
-7.5
当堂练习
B A 随堂检测B D 5.若a是有理数,则下面说法正确的是( )A.|a|一定是正数 B.|-a|一定是正数C.-|a|一定是正数 D.|a|一定是非负数6.已知|a|=0,则a=____.7.若a位于数轴上原点的左侧,且|a|=3.14,则a=_________.8.【四川攀枝花中考】|-3|的相反数是______.D 0 -3.14 -3 10.如果|x|=|-5|,那么x等于( )A.5 B.-5C.5或-5 D.以上都不对11.若a为有理数,且|a|=-a,那么a是( )A.正数 B.负数 C.非负数 D.非正数C D 12.【易错题】下列说法中,正确的是( )A.一个有理数的绝对值不小于它自身B.若两个有理数的绝对值相等,则这两个数相等C.若两个有理数的绝对值相等,则这两个数互为相反数D.-a的绝对值等于aA 解析:正数和0的绝对值是它本身,负数的绝对值是它的相反数,所以一个有理数的绝对值不小于它自身,A正确;若两个有理数的绝对值相等,则这两个数相等或互为相反数,B、C错误;当a<0时,-a的绝对值等于-a,D错误.13.化简:|π-4|+|3-π|=____.14.若|m-n+2|+|m-3|=0,求m+n的值.1 解:因为|m-n+2|≥0,|m-3|≥0,|m-n+2|+|m-3|=0,所以|m-n+2|=0,|m-3|=0,所以m=3,n=5,m+n=8.15.在各项国际乒乓球大赛中,国际乒联对乒乓球的直径有严格的规定.现有5个乒乓球,测量它们的直径,超过标准直径的毫米数记为正数,不足的记为负数.检测结果如下:A.+0.1毫米;B.-0.3毫米;C.+0.2毫米;D.-0.05毫米;E.-0.1毫米.你认为选哪一个乒乓球用于比赛最好呢?为什么?解:选乒乓球D用于比赛最好.理由:因为|+0.1|=0.1,|-0.3|=0.3,|+0.2|=0.2,|-0.05|=0.05,|-0.1|=0.1,0.05<0.1<0.2<0.3,所以乒乓球D的直径最接近于标准直径,选乒乓球D用于比赛最好.(2)当a是负数时,|a|=
2.(1)当a是正数时,|a|=
(3)当a=0时,|a|=
a
-a
0
课堂小结
数轴上表示数a的点与原点的距离叫做数a的绝对值。
3.互为相反数的两个数的绝对值相等
