1.3.2 有理数的加减混合运算(第2课时) 课件(共31张PPT)
文档属性
| 名称 | 1.3.2 有理数的加减混合运算(第2课时) 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 11:13:17 | ||
图片预览











文档简介
(共31张PPT)
1.3.2 有理数的加减混合运算
(第2课时)
第 1 章 有 理 数
七年级上册数学人教版
目录
加减混合运算
01
加减混合运算应用
02
学习目标
1.理解加减法统一成加法的意义,能熟练地进行有理数加减法的混合运算.(重点)
2.通过加减法的相互转化,培养应变能力、计算能力.(难点)
一口深3.5米的深井,一只青蛙从井底沿井壁往上爬,第一次爬了0.7米又下滑了0.1米,第二次往上爬了0.42米又下滑了0.15米,第三次往上爬了1.25米又下滑了0.2米,第四次往上爬了0.75米又下滑了0.1米,第五次往上爬了0.65米.
问题:小青蛙爬出井了吗?
情境引入
例1 计算: (-20)+(+3)-(-5)-(+7)
(-20)+(+3)+(+5)+(-7)
典例精析
这个算式中有加法,也有减法.可以根据有理数减法法则,把它改写为
分析:
使问题转化为几个有理数的加法.
教材23页例5
解:
这里使用了哪些运算律?
有理数加法的交换律、结合律
要点归纳:引入相反数后,加减混合运算可以统一为加法运算:
算式 是 , ,
, 这四个数的和.
为书写简单,省略算式中的括号和加号写为
( )
我们可以读作 的和,或读作 加 加 减 .
-20 3
5 -7
-20+3+5-7
负20、 正3、正5、负7
负20 3 5 7
大胆探究:
在符号简写这个环节,有什么小窍门么?
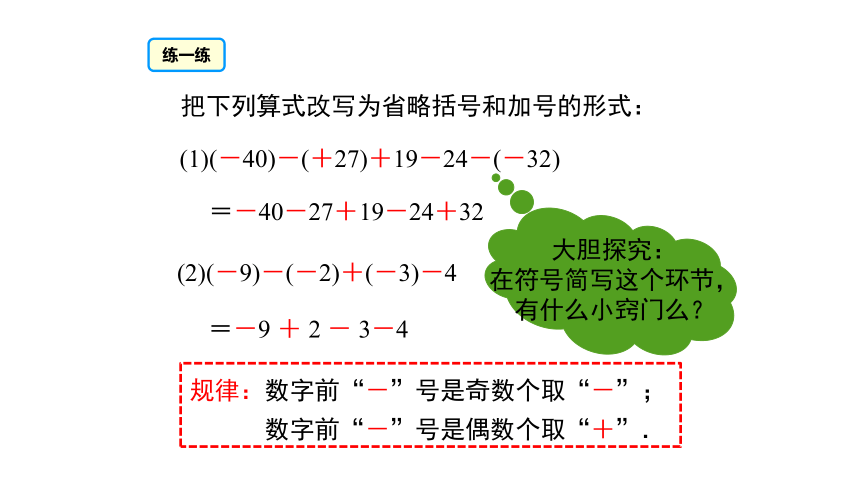
(1)(-40)-(+27)+19-24-(-32)
练一练
把下列算式改写为省略括号和加号的形式:
(2)(-9)-(-2)+(-3)-4
=-40-27+19-24+32
=-9 + 2 - 3-4
规律:数字前“-”号是奇数个取“-”;
数字前“-”号是偶数个取“+”.
例2 计算:(-2)+(+30)-(-15)-(+27)
解:原式=(-2)+(+30)+(+15)+(-27)
=[(-2)+(-27)]+[(+30)+(+15)]
=(-29)+(+45)
=16
减法转化成加法
按有理数加法法则计算
方法一:减法变加法
典例精析
解:原式=-2+30+15-27
=-2-27+30+15
=-2+(-27)+45
=-29+45
省略括号
运用加法交换律使同号两数分别相加
按有理数加法法则计算
=-(29-45)
=16
方法二:(去括号法)
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算.
归纳总结
1.计算:(–7)–(+5)+(–4)–(–10).
解:(–7)–(+5)+(–4)–(–10)
= (–7)+(–5)+(–4)+10
= (–16)+10
= –6.
典例精练
教材24页练习(3)
解:(1)原式 = 3.1.(2)原式 = . (3)原式 = 8.
(4)原式 = 0.1.(5)原式 = .(6)原式 = 0.
2.计算:
(1)-4.2+5.7-8.4+10;
(3)12-(-18)+(-7)-15; (4)4.7-(-8.9)-7.5+(-6);
教材25页习题1.3第5题
例3.2017年中国空军在南海进行了军事演习,一架飞机作特技表演,起飞后的高度变化如下表:
此时飞机比起飞点高了多少千米
高度变化 上升4.5千米 下降3.2千米 上升1.1千米 下降1.4千米
记 作 +4.5千米 -3.2千米 +1.1千米 -1.4千米
解:4.5+(-3.2)+1.1+(-1.4)
=(4.5+1.1)+[(-3.2)+(-1.4)]
=(4.5+1.1)+[(-3.2)+(-1.4)]
=5.6+(-4.6)=1(千米)
答:此时飞机比起飞点高了1千米.
典例精析
星期 一 二 三 四 五 六 日
与前一天的价格涨跌情况(元) +0.2 ﹣0.3 +0.5 +0.2 ﹣0.3 +0.4 ﹣0.1
3.(2021秋 濮阳期末)如表为本周内某农产品每天的批发价格
比前一天的涨跌情况(上周末该农产品的批发价格为2.7元/斤).
注:正号表示价格比前一天上涨,负号表示价格比前一天下跌.
(1)本周哪天该农产品的批发价格最高,批发价格是多少元/斤?
本周哪天该农产品的批发价格最低,批发价格是多少元/斤?
(2)与上周末相比,本周末该农产品的批发价格是上升了还是下降了?
变化了多少?
典例精练
【解答】解:(1)星期一的价格:2.7+(+0.2)=2.9(元);
星期二的价格:2.9+(﹣0.3)=2.6(元);
星期三的价格:2.6+(+0.5)=3.1(元);
星期四的价格:3.1+(+0.2)=3.3(元);
星期五的价格:3.3+(﹣0.3)=3(元);
星期六的价格:3+(+0.4)=3.4(元);
星期日的价格:3.4+(﹣0.1)=3.3(元);
故本周星期六,该农产品的批发价格最高,批发价格是3.4元;
本周星期二,该农产品的批发价格最低,批发价格是2.6元.
(2)由(1)可知,星期日的价格为3.3元,3.3>2.7,3.3﹣2.7=0.6(元),
答:与上周末相比,本周末该农产品的批发价格是上升了,上升了0.6元.
第一天 第二天 第三天 第四天 第五天 第六天 第七天
路程(km) ﹣7 ﹣12 ﹣13 0 ﹣17 +40 +9
4.(2021秋 玉门市期末)随着人们生活水平的提高,家用轿车越来越多地
进入家庭,小亮家中买了一辆小轿车,他连续记录了7天中每天行驶
的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记
为“﹣”,刚好50km的记为“0”.
(1)请求出这7天中平均每天行驶多少千米?
(2)若每行驶50km需用汽油4升,汽油价6.8元/升,计算小亮家这7天的汽油费用
大约是多少元?
在数轴上,点A,B分别表示数a,b,利用有理数的减法,分别计算下面情况下点A,B之间的距离:
(1)a=2,b=6
两点之间的距离
等于这两个数差的绝对值,即AB=|a-b|.
b-a=6-0=6
b-a=6-2=4
a-b=2-(-6)=8
|a-b|=|(-2)-(-6)|=4
(2)a=0,b=6
(3)a=2,b=-6
(4)a=-2,b=-6
规律探究
例4.(2021秋 魏都区校级期中)数轴是一个非常重要的数学工具,它使数和数轴上的
点建立起一一对应的关系,揭示了数与点之间的内在联系,它是“数形结合”的基础,
我们知道|2|=|2﹣0|,它在数轴上的意义是表示数2的点与原点(即表示0的点)之间的距离,
|5﹣2|可理解为5与2两数在数轴上所对应的两点之间的距离:|5+2|可以看作|5﹣(﹣2)|,
表示5与﹣2两数在数轴上所对应的两点之间的距离.
(1)数轴上表示3和﹣1的两点之间的距离的式子是 .
(2)探索:
①若|x﹣4|=3,则x= .
②若使x所表示的点到表示4和﹣1的点的距离之和为5.所有符合条件的整数为 .
(3)进一步探究:|x+1|+|x﹣6|的最小值为 .
(4)能力提升:当|x+1+|x﹣4+|x﹣9|的值最小时,x的值为 .
典例精析
|3﹣(﹣1)|;
1或7;
4、3 、2、1、0、﹣1;
7;
4.
1. 某市某一天的最高气温为2℃,最低气温为–8℃,则这天的最高气温比最低气温高( )
A.10℃ B.6℃
C.–6℃ D.–10℃
2. 计算:6 – (3–5)= .
A
8
中考链接
D 2019 11 当堂练习4.计算:(1)23-17-(-7)+(-16);解:原式=23-17+7-16=(23+7)+(-17-16)=30+(-33)=-3.(2)(-26.54)+(-6.4)-18.54+6.4;解:原式=(-26.54-18.54)+[(-6.4)+6.4]=-45.08+0=-45.08.5.某人用400元购买了8套儿童服装,准备以一定价格出售,如果每套儿童服装以54元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,-3,+2,+1,-2,-3,0,-2,当卖完这8套儿童服装后是盈利还是亏损?盈利(亏损)多少钱?解:2-3+2+1-2-3+0-2=-5,54×8-5=427(元),427-400=27(元).即当卖完这8套儿童服装后是盈利,盈利27元.0 8.小明计划在假期每天做5道数学题,超过的题数记为正数,不足的题数记为负数.他十天中做的题数记录如下:3,5,-4,2,-1,7,0,-3,8,10,则小明这十天共做了多少道数学题?解:3+5+(-4)+2+(-1)+7+0+(-3)+8+10=(3+5+2+7+0+8+10)+[(-4)+(-1)+(-3)]=35+(-8)=27,5×10+27=77(道).即小明这十天共做了77道数学题.解:(1)根据题意,得300+35=335(辆),则本周星期三生产了335辆摩托车.(2)根据题意,得-50-72+35+42+10=-35(辆),则本周总生产量与计划生产量相比,减少了.(3)根据题意,得42-(-72)=42+72=114(辆),则产量最多的一天比产量最少的一天多生产了114辆.有依次排列的3个数:3,9,8.对任何相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,-1,8,这称为第一次操作;做第二次同样的操作后,也可产生一个新数串:3,3,6,3,9,-10,-1,9,8.继续操作下去,问:(1)第一次操作后,增加的新数之和是多少?(2)第二次操作后所得到的数串比第一次操作后所得的数串增加的新数之和是多少?(3)猜想第100次操作后所得到的数串比第99次操作后所得的数串增加的新数之和是多少?(4)利用你的猜想,计算第100次操作以后产生的新数串的所有数之和.能力提升解:(1)增加的新数之和为6+(-1)=5.(2)3+3-10+9=5,即第二次操作后所得到的数串比第一次操作后所得的数串增加的新数之和是5.(3)根据前两次的计算,猜想第100次操作后所得到的数串比第99次操作后所得的数串增加的新数之和也是5.(4)3+9+8+5×100=520,即第100次操作以后产生的新数串的所有数之和是520.有理数加减法混合运算的步骤为:
方法一:减法转化成加法
1.减法变加法:a+b-c=a+b+(-c)
2.运用加法交换律使同号两数分别相加;
3.按有理数加法法则计算
方法二:省略括号法
1.省略括号;
2.同号放一起;
3.进行加减运算.
课堂小结
1.3.2 有理数的加减混合运算
(第2课时)
第 1 章 有 理 数
七年级上册数学人教版
目录
加减混合运算
01
加减混合运算应用
02
学习目标
1.理解加减法统一成加法的意义,能熟练地进行有理数加减法的混合运算.(重点)
2.通过加减法的相互转化,培养应变能力、计算能力.(难点)
一口深3.5米的深井,一只青蛙从井底沿井壁往上爬,第一次爬了0.7米又下滑了0.1米,第二次往上爬了0.42米又下滑了0.15米,第三次往上爬了1.25米又下滑了0.2米,第四次往上爬了0.75米又下滑了0.1米,第五次往上爬了0.65米.
问题:小青蛙爬出井了吗?
情境引入
例1 计算: (-20)+(+3)-(-5)-(+7)
(-20)+(+3)+(+5)+(-7)
典例精析
这个算式中有加法,也有减法.可以根据有理数减法法则,把它改写为
分析:
使问题转化为几个有理数的加法.
教材23页例5
解:
这里使用了哪些运算律?
有理数加法的交换律、结合律
要点归纳:引入相反数后,加减混合运算可以统一为加法运算:
算式 是 , ,
, 这四个数的和.
为书写简单,省略算式中的括号和加号写为
( )
我们可以读作 的和,或读作 加 加 减 .
-20 3
5 -7
-20+3+5-7
负20、 正3、正5、负7
负20 3 5 7
大胆探究:
在符号简写这个环节,有什么小窍门么?
(1)(-40)-(+27)+19-24-(-32)
练一练
把下列算式改写为省略括号和加号的形式:
(2)(-9)-(-2)+(-3)-4
=-40-27+19-24+32
=-9 + 2 - 3-4
规律:数字前“-”号是奇数个取“-”;
数字前“-”号是偶数个取“+”.
例2 计算:(-2)+(+30)-(-15)-(+27)
解:原式=(-2)+(+30)+(+15)+(-27)
=[(-2)+(-27)]+[(+30)+(+15)]
=(-29)+(+45)
=16
减法转化成加法
按有理数加法法则计算
方法一:减法变加法
典例精析
解:原式=-2+30+15-27
=-2-27+30+15
=-2+(-27)+45
=-29+45
省略括号
运用加法交换律使同号两数分别相加
按有理数加法法则计算
=-(29-45)
=16
方法二:(去括号法)
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算.
归纳总结
1.计算:(–7)–(+5)+(–4)–(–10).
解:(–7)–(+5)+(–4)–(–10)
= (–7)+(–5)+(–4)+10
= (–16)+10
= –6.
典例精练
教材24页练习(3)
解:(1)原式 = 3.1.(2)原式 = . (3)原式 = 8.
(4)原式 = 0.1.(5)原式 = .(6)原式 = 0.
2.计算:
(1)-4.2+5.7-8.4+10;
(3)12-(-18)+(-7)-15; (4)4.7-(-8.9)-7.5+(-6);
教材25页习题1.3第5题
例3.2017年中国空军在南海进行了军事演习,一架飞机作特技表演,起飞后的高度变化如下表:
此时飞机比起飞点高了多少千米
高度变化 上升4.5千米 下降3.2千米 上升1.1千米 下降1.4千米
记 作 +4.5千米 -3.2千米 +1.1千米 -1.4千米
解:4.5+(-3.2)+1.1+(-1.4)
=(4.5+1.1)+[(-3.2)+(-1.4)]
=(4.5+1.1)+[(-3.2)+(-1.4)]
=5.6+(-4.6)=1(千米)
答:此时飞机比起飞点高了1千米.
典例精析
星期 一 二 三 四 五 六 日
与前一天的价格涨跌情况(元) +0.2 ﹣0.3 +0.5 +0.2 ﹣0.3 +0.4 ﹣0.1
3.(2021秋 濮阳期末)如表为本周内某农产品每天的批发价格
比前一天的涨跌情况(上周末该农产品的批发价格为2.7元/斤).
注:正号表示价格比前一天上涨,负号表示价格比前一天下跌.
(1)本周哪天该农产品的批发价格最高,批发价格是多少元/斤?
本周哪天该农产品的批发价格最低,批发价格是多少元/斤?
(2)与上周末相比,本周末该农产品的批发价格是上升了还是下降了?
变化了多少?
典例精练
【解答】解:(1)星期一的价格:2.7+(+0.2)=2.9(元);
星期二的价格:2.9+(﹣0.3)=2.6(元);
星期三的价格:2.6+(+0.5)=3.1(元);
星期四的价格:3.1+(+0.2)=3.3(元);
星期五的价格:3.3+(﹣0.3)=3(元);
星期六的价格:3+(+0.4)=3.4(元);
星期日的价格:3.4+(﹣0.1)=3.3(元);
故本周星期六,该农产品的批发价格最高,批发价格是3.4元;
本周星期二,该农产品的批发价格最低,批发价格是2.6元.
(2)由(1)可知,星期日的价格为3.3元,3.3>2.7,3.3﹣2.7=0.6(元),
答:与上周末相比,本周末该农产品的批发价格是上升了,上升了0.6元.
第一天 第二天 第三天 第四天 第五天 第六天 第七天
路程(km) ﹣7 ﹣12 ﹣13 0 ﹣17 +40 +9
4.(2021秋 玉门市期末)随着人们生活水平的提高,家用轿车越来越多地
进入家庭,小亮家中买了一辆小轿车,他连续记录了7天中每天行驶
的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记
为“﹣”,刚好50km的记为“0”.
(1)请求出这7天中平均每天行驶多少千米?
(2)若每行驶50km需用汽油4升,汽油价6.8元/升,计算小亮家这7天的汽油费用
大约是多少元?
在数轴上,点A,B分别表示数a,b,利用有理数的减法,分别计算下面情况下点A,B之间的距离:
(1)a=2,b=6
两点之间的距离
等于这两个数差的绝对值,即AB=|a-b|.
b-a=6-0=6
b-a=6-2=4
a-b=2-(-6)=8
|a-b|=|(-2)-(-6)|=4
(2)a=0,b=6
(3)a=2,b=-6
(4)a=-2,b=-6
规律探究
例4.(2021秋 魏都区校级期中)数轴是一个非常重要的数学工具,它使数和数轴上的
点建立起一一对应的关系,揭示了数与点之间的内在联系,它是“数形结合”的基础,
我们知道|2|=|2﹣0|,它在数轴上的意义是表示数2的点与原点(即表示0的点)之间的距离,
|5﹣2|可理解为5与2两数在数轴上所对应的两点之间的距离:|5+2|可以看作|5﹣(﹣2)|,
表示5与﹣2两数在数轴上所对应的两点之间的距离.
(1)数轴上表示3和﹣1的两点之间的距离的式子是 .
(2)探索:
①若|x﹣4|=3,则x= .
②若使x所表示的点到表示4和﹣1的点的距离之和为5.所有符合条件的整数为 .
(3)进一步探究:|x+1|+|x﹣6|的最小值为 .
(4)能力提升:当|x+1+|x﹣4+|x﹣9|的值最小时,x的值为 .
典例精析
|3﹣(﹣1)|;
1或7;
4、3 、2、1、0、﹣1;
7;
4.
1. 某市某一天的最高气温为2℃,最低气温为–8℃,则这天的最高气温比最低气温高( )
A.10℃ B.6℃
C.–6℃ D.–10℃
2. 计算:6 – (3–5)= .
A
8
中考链接
D 2019 11 当堂练习4.计算:(1)23-17-(-7)+(-16);解:原式=23-17+7-16=(23+7)+(-17-16)=30+(-33)=-3.(2)(-26.54)+(-6.4)-18.54+6.4;解:原式=(-26.54-18.54)+[(-6.4)+6.4]=-45.08+0=-45.08.5.某人用400元购买了8套儿童服装,准备以一定价格出售,如果每套儿童服装以54元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,-3,+2,+1,-2,-3,0,-2,当卖完这8套儿童服装后是盈利还是亏损?盈利(亏损)多少钱?解:2-3+2+1-2-3+0-2=-5,54×8-5=427(元),427-400=27(元).即当卖完这8套儿童服装后是盈利,盈利27元.0 8.小明计划在假期每天做5道数学题,超过的题数记为正数,不足的题数记为负数.他十天中做的题数记录如下:3,5,-4,2,-1,7,0,-3,8,10,则小明这十天共做了多少道数学题?解:3+5+(-4)+2+(-1)+7+0+(-3)+8+10=(3+5+2+7+0+8+10)+[(-4)+(-1)+(-3)]=35+(-8)=27,5×10+27=77(道).即小明这十天共做了77道数学题.解:(1)根据题意,得300+35=335(辆),则本周星期三生产了335辆摩托车.(2)根据题意,得-50-72+35+42+10=-35(辆),则本周总生产量与计划生产量相比,减少了.(3)根据题意,得42-(-72)=42+72=114(辆),则产量最多的一天比产量最少的一天多生产了114辆.有依次排列的3个数:3,9,8.对任何相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,-1,8,这称为第一次操作;做第二次同样的操作后,也可产生一个新数串:3,3,6,3,9,-10,-1,9,8.继续操作下去,问:(1)第一次操作后,增加的新数之和是多少?(2)第二次操作后所得到的数串比第一次操作后所得的数串增加的新数之和是多少?(3)猜想第100次操作后所得到的数串比第99次操作后所得的数串增加的新数之和是多少?(4)利用你的猜想,计算第100次操作以后产生的新数串的所有数之和.能力提升解:(1)增加的新数之和为6+(-1)=5.(2)3+3-10+9=5,即第二次操作后所得到的数串比第一次操作后所得的数串增加的新数之和是5.(3)根据前两次的计算,猜想第100次操作后所得到的数串比第99次操作后所得的数串增加的新数之和也是5.(4)3+9+8+5×100=520,即第100次操作以后产生的新数串的所有数之和是520.有理数加减法混合运算的步骤为:
方法一:减法转化成加法
1.减法变加法:a+b-c=a+b+(-c)
2.运用加法交换律使同号两数分别相加;
3.按有理数加法法则计算
方法二:省略括号法
1.省略括号;
2.同号放一起;
3.进行加减运算.
课堂小结
