1.3.2 有理数减法(第1课时) 课件(共26张PPT)
文档属性
| 名称 | 1.3.2 有理数减法(第1课时) 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 619.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 11:15:42 | ||
图片预览







文档简介
(共26张PPT)
1.3.2 有理数减法
(第1课时)
第 1 章 有 理 数
七年级上册数学人教版
目录
有理数减法法则
01
有理数减法的应用
02
学习目标:
1. 知道有理数的减法法则.
2. 能熟练地运用有理数的减法法则进行有理数的减法运算.(重点)
3. 通过加与减两种运算的对立统一关系,建立“转化”的数学思想.(难点)
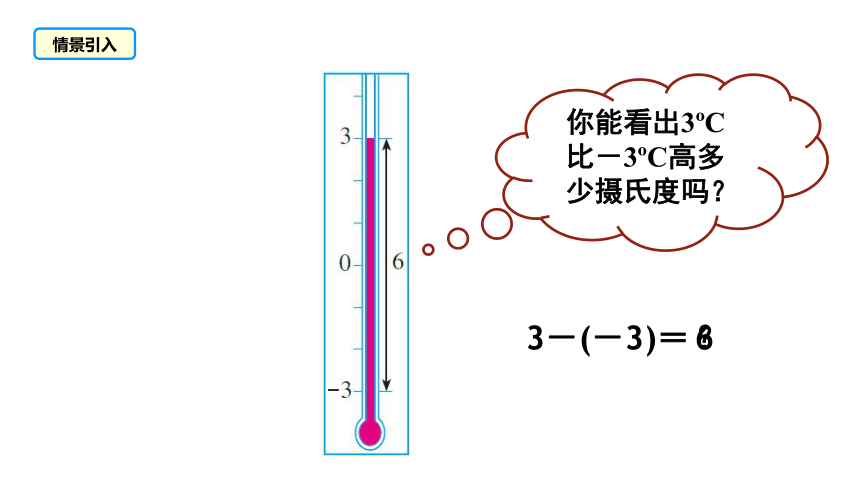
你能看出3 C比-3 C高多少摄氏度吗?
3-(-3)=
?
6
情景引入
1. 有理数减法法则
从中又能有新的发现吗?
计算:
1
1
8
8
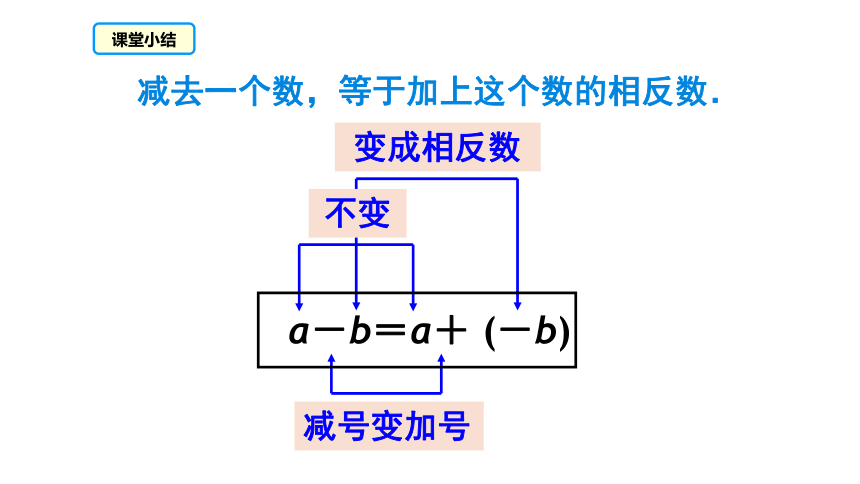
变成相反数
不变
减号变加号
a-b=a+ (-b)
减去一个数,等于加上这个数的相反数.
课堂小结
(1)(-32)-(+5);
=-32+(-5)
=7.3+6.8
=-2+25
=12+(-21)
(2)7.3-(-6.8);
(3)(-2)-(-25);
(4)12-21.
=-37
=14.1
=23
=-9
典例精析
例1 计算:
填空.
(1) +3=10;
7
(-3)
13
19
(2)30+ =27;
(3) +(-3)=10;
(4)-13+ =6.
典例精练
练习:教材第23页
1.计算:
(1) 6-9; (2) (+4)-(-7);
(3)(-5)-(-8); (4) 0 -(-5);
(5)(-2.5)-5.9 ; (6) 1.9 -(-0.6).
-3
11
3
5
-8.4
2.5
2.计算:
(1)比2 C 低 8 C 的温度;
(2)比 -3 C 低 6 C 的温度.
解:(1)2-8=- 6 ℃;
(2)-3-6=- 9 ℃
3.填空.
(1)____+11=27 (2)7+_______=4
(3)(-9)+____=9 (4)12+_______=0
(5)(-8)+_____=-15(6)__+(-13)=6
教材第26页拓展延伸
16
(-3)
18
(-12)
(-7)
19
例2 计算:
典例精析
例3 已知│a│= 5,│b│= 3,且a>0,b<0,则a-b= .
解析:由│a│= 5,│b│= 3,得a=± 5,b= ±3.
又因为a>0,b<0,所以a= 5,b= -3.
所以a-b=5-(-3)=5+3=8.
8
2. 有理数减法的应用
典例精析1.【山东淄博中考】比-2小1的数是( )A.-3 B.-1 C.1 D.32.|(-3)-5|等于( )A.-8 B.-2 C.2 D.83.下列计算正确的是( )A.(-14)-(+5)=-9 B.0-(-3)=3C.(-3)-(-3)=-6 D.|5-3|=-(5-3)A D B 当堂练习4.某市有一天的最高气温为2 ℃,最低气温为-8 ℃,则这天的最高气温比最低气温高( )A.10 ℃ B.6 ℃ C.-6 ℃ D.-10 ℃5.下列说法中,正确的是( )A.两数相减,被减数一定大于减数B.0减去一个数仍得这个数C.互为相反数的两个数的差为0D.减去一个正数,差一定小于被减数A D 6.填空:(1)-4-(-3.2)= -4+ = ;
(2)(-35)-(+12)= .
7.计算(口答):
(1)6-9; (2)(+4)-(-7);
(3)(-5)-(-8) ; (4)(-4)-9;
(5)0-(-5); (6)0-5.
答案:6.(1)3.2 -0.8 (2)-47
7.(1)-3 (2)11 (3)3 (4)-13
(5)5 (6)-5
1.一天早晨的气温是-3 ℃,中午上升到15 ℃,则这天中午比早晨的气温上升了( )A.15 ℃ B.18 ℃ C.-3 ℃ D.-18 ℃2.如果四个有理数之和是12,其中三个数是-10,+8,-6,则第四个数是( )A.+8 B.+11 C.+12 D.+20B D 随堂检测3.下列结论错误的是( )A.若a>0,b<0,则a-b>0B.若a<b,b>0,则a-b<0C.若a<0,b<0,则a-(-b)<0D.若a<0,b<0,且|a|>|b|,则a-b>04.从海拔12 m的地方乘电梯到海拔-10 m的地方,一共下降了_____m.5.已知一个数是-2,另一个数比-2的相反数小3,则这两个数差的绝对值为____.D 22 1
6.计算.
(1)(-3)-(-4);
=(-3)+4
=(-5)+(-10)
=9+21
=1.3+2.7
=6.38+2.62
=-2.5+(-4.5)
(2)(-5)-10;
(3)9-(-21);
(4)1.3-(-2.7);
(5)6.38-(-2.62);
(6)-2.5-4.5;
=1
=-15
=30
=4
=9
=-7
变成相反数
不变
减号变加号
a-b=a+ (-b)
减去一个数,等于加上这个数的相反数.
课堂小结
减数、被减数、差之间的关系.
(1)被减数与差的大小关系:
②一个数减去0,所得的差等于被减数,
即a-0=a;
③一个数减去一个负数,所得的差大于被减数,
即a-负数>a.
①一个数减去一个正数,所得的差小于被
减数,即a-正数(2)注意
②不论是正数、负数或零,都符合有理数减
法法则.在使用法则时,注意减号变加号的
同时,把减数变成它的相反数,而被减数不
变.
③通过这个法则,可以把减法统一成加法.
①有理数减法法则是一个转化法则,减数变
为它的相反数,从而减法转化为加法.
1.3.2 有理数减法
(第1课时)
第 1 章 有 理 数
七年级上册数学人教版
目录
有理数减法法则
01
有理数减法的应用
02
学习目标:
1. 知道有理数的减法法则.
2. 能熟练地运用有理数的减法法则进行有理数的减法运算.(重点)
3. 通过加与减两种运算的对立统一关系,建立“转化”的数学思想.(难点)
你能看出3 C比-3 C高多少摄氏度吗?
3-(-3)=
?
6
情景引入
1. 有理数减法法则
从中又能有新的发现吗?
计算:
1
1
8
8
变成相反数
不变
减号变加号
a-b=a+ (-b)
减去一个数,等于加上这个数的相反数.
课堂小结
(1)(-32)-(+5);
=-32+(-5)
=7.3+6.8
=-2+25
=12+(-21)
(2)7.3-(-6.8);
(3)(-2)-(-25);
(4)12-21.
=-37
=14.1
=23
=-9
典例精析
例1 计算:
填空.
(1) +3=10;
7
(-3)
13
19
(2)30+ =27;
(3) +(-3)=10;
(4)-13+ =6.
典例精练
练习:教材第23页
1.计算:
(1) 6-9; (2) (+4)-(-7);
(3)(-5)-(-8); (4) 0 -(-5);
(5)(-2.5)-5.9 ; (6) 1.9 -(-0.6).
-3
11
3
5
-8.4
2.5
2.计算:
(1)比2 C 低 8 C 的温度;
(2)比 -3 C 低 6 C 的温度.
解:(1)2-8=- 6 ℃;
(2)-3-6=- 9 ℃
3.填空.
(1)____+11=27 (2)7+_______=4
(3)(-9)+____=9 (4)12+_______=0
(5)(-8)+_____=-15(6)__+(-13)=6
教材第26页拓展延伸
16
(-3)
18
(-12)
(-7)
19
例2 计算:
典例精析
例3 已知│a│= 5,│b│= 3,且a>0,b<0,则a-b= .
解析:由│a│= 5,│b│= 3,得a=± 5,b= ±3.
又因为a>0,b<0,所以a= 5,b= -3.
所以a-b=5-(-3)=5+3=8.
8
2. 有理数减法的应用
典例精析1.【山东淄博中考】比-2小1的数是( )A.-3 B.-1 C.1 D.32.|(-3)-5|等于( )A.-8 B.-2 C.2 D.83.下列计算正确的是( )A.(-14)-(+5)=-9 B.0-(-3)=3C.(-3)-(-3)=-6 D.|5-3|=-(5-3)A D B 当堂练习4.某市有一天的最高气温为2 ℃,最低气温为-8 ℃,则这天的最高气温比最低气温高( )A.10 ℃ B.6 ℃ C.-6 ℃ D.-10 ℃5.下列说法中,正确的是( )A.两数相减,被减数一定大于减数B.0减去一个数仍得这个数C.互为相反数的两个数的差为0D.减去一个正数,差一定小于被减数A D 6.填空:(1)-4-(-3.2)= -4+ = ;
(2)(-35)-(+12)= .
7.计算(口答):
(1)6-9; (2)(+4)-(-7);
(3)(-5)-(-8) ; (4)(-4)-9;
(5)0-(-5); (6)0-5.
答案:6.(1)3.2 -0.8 (2)-47
7.(1)-3 (2)11 (3)3 (4)-13
(5)5 (6)-5
1.一天早晨的气温是-3 ℃,中午上升到15 ℃,则这天中午比早晨的气温上升了( )A.15 ℃ B.18 ℃ C.-3 ℃ D.-18 ℃2.如果四个有理数之和是12,其中三个数是-10,+8,-6,则第四个数是( )A.+8 B.+11 C.+12 D.+20B D 随堂检测3.下列结论错误的是( )A.若a>0,b<0,则a-b>0B.若a<b,b>0,则a-b<0C.若a<0,b<0,则a-(-b)<0D.若a<0,b<0,且|a|>|b|,则a-b>04.从海拔12 m的地方乘电梯到海拔-10 m的地方,一共下降了_____m.5.已知一个数是-2,另一个数比-2的相反数小3,则这两个数差的绝对值为____.D 22 1
6.计算.
(1)(-3)-(-4);
=(-3)+4
=(-5)+(-10)
=9+21
=1.3+2.7
=6.38+2.62
=-2.5+(-4.5)
(2)(-5)-10;
(3)9-(-21);
(4)1.3-(-2.7);
(5)6.38-(-2.62);
(6)-2.5-4.5;
=1
=-15
=30
=4
=9
=-7
变成相反数
不变
减号变加号
a-b=a+ (-b)
减去一个数,等于加上这个数的相反数.
课堂小结
减数、被减数、差之间的关系.
(1)被减数与差的大小关系:
②一个数减去0,所得的差等于被减数,
即a-0=a;
③一个数减去一个负数,所得的差大于被减数,
即a-负数>a.
①一个数减去一个正数,所得的差小于被
减数,即a-正数
②不论是正数、负数或零,都符合有理数减
法法则.在使用法则时,注意减号变加号的
同时,把减数变成它的相反数,而被减数不
变.
③通过这个法则,可以把减法统一成加法.
①有理数减法法则是一个转化法则,减数变
为它的相反数,从而减法转化为加法.
