1.4.1有理数乘法的运算律及其应用(第2课时) 课件(共36张PPT)
文档属性
| 名称 | 1.4.1有理数乘法的运算律及其应用(第2课时) 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 900.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 11:28:49 | ||
图片预览










文档简介
1.4.1有理数乘法的运算律
及运用(第2课时)
第 1 章 有 理 数
七年级上册数学人教版
目录
有理数乘法运算律
01
乘法运算律应用
02
学习目标
1.掌握乘法的分配律,并能灵活的运用.(难点)
2.掌握有理数乘法的运算律,并利用运算律简化乘法运算.(重点)
问题引入
1.有理数的乘法法则是什么?
3.小学时候大家学过乘法的哪些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和零相乘,都得0
乘法交换律、乘法结合律、乘法分配律
2.如何进行多个有理数的乘法运算?
(1)定号(奇负偶正) (2)算值(积的绝对值)
问题1 观察下列各式,它们的积是正的还是负的?
,
,
,
思考:几个不是0
的数相乘,积的符号
.
组卷组卷网
网
归纳:
几个不是0的数相乘,负因数的个数是______
时,积是正数;负因数的个数是_________时,积
是负数.
偶数
奇数
典例精析
几个不等于零的数相乘,积的正负号由负因数的个数决定,当负因数的个数为奇数时,积为负;当负因数的个数为偶数时,积为正.
几个不等于零的数相乘,首先确定积的正负号,然后把绝对值相乘。
归纳总结
几个数相乘,如果其中有因数为0,积等于____.
问题2
你能看出下式的结果吗?如果能,请说明理由学科网
0
1.有理数乘法运算律
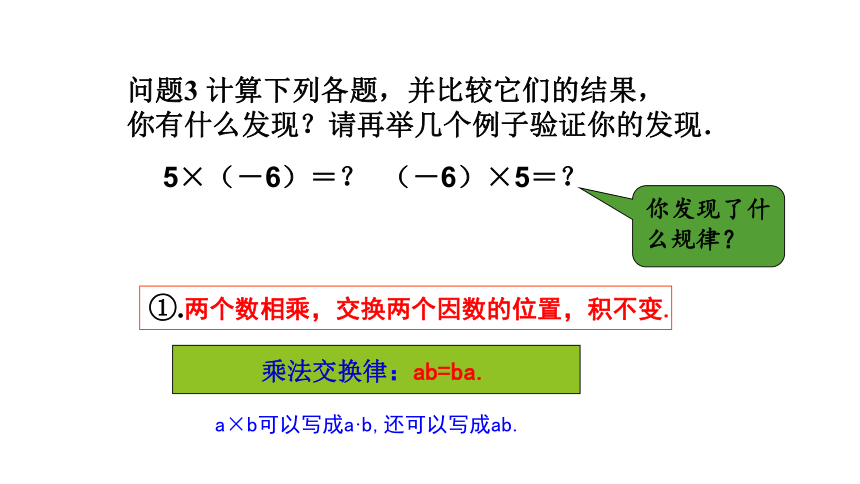
问题3 计算下列各题,并比较它们的结果,
你有什么发现?请再举几个例子验证你的发现.
5×(-6)=? (-6)×5=?
你发现了什么规律?
①.两个数相乘,交换两个因数的位置,积不变.
乘法交换律:ab=ba.
a×b可以写成a·b,还可以写成ab.
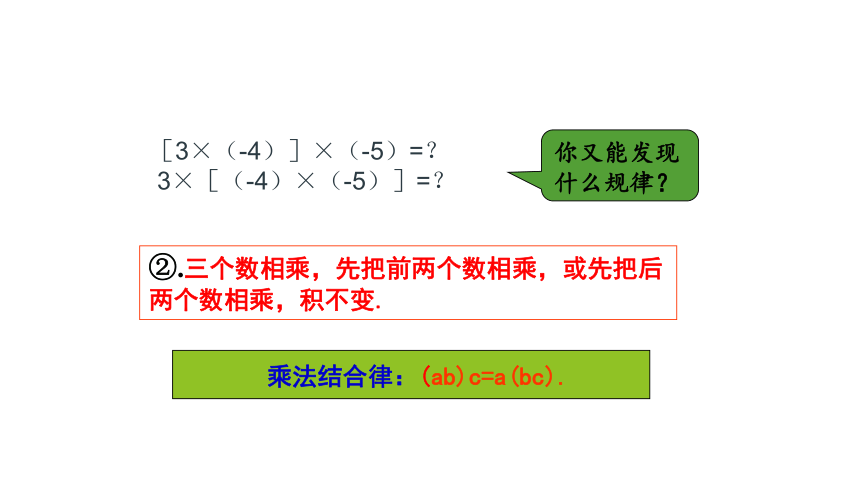
[3×(-4)]×(-5)=?
3×[(-4)×(-5)]=?
你又能发现什么规律?
②.三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变.
乘法结合律:(ab)c=a(bc).
5×[3+(-7)]=
5×3+5×(-7) =
5×(-4) =-20
15+(-35)=-20
③一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加. Z```xxk
乘法分配律:a(b+c)=ab+ac.
2. 乘法运算律应用
典例精析
例2 计算:(-85)×(-25)×(-4)
解:原式=(-85)×[(-25)×(-4)]
=(-85)×100
=-8500
1.计算: (-8)×(-12)×(-0.125)×(- )×(-0.1)
1
3
解:原式=-8×(-0.125) ×(-12) ×(- ) ×(-0.1)
=[-8×(-0.125)] ×[(-12) ×(- )] ×(-0.1)
=1×4×(-0.1)
=-0.4
典例精练
( + - )×12
例3 用两种方法计算
1
2
1
6
1
4
解法1:
( + - )×12
3
12
2
12
6
12
原式=
1
12
=- ×12
=-1
解法2:
原式=
×12 + ×12- ×12
1
4
1
6
1
2
=3+2-6
=-1
典例精析
解法有错吗?错在哪里?
? ? ?
__ __ __
(-24)×( - + - )
5
8
1
6
3
4
1
3
解:
原式=
-24× -24× +24× -24×
5
8
1
6
3
4
1
3
2.计算:
=-8-18+4-15
=-41+4
=-37
观察与思考
正确解法:
特别提醒:
1.不要漏掉符号,
2.不要漏乘.
_____ ______ ______ ______
(-24)×( - + - )
5
8
1
6
3
4
1
3
=-8+18-4+15
=-12+33
=21
=(-24)× +(-24)×(- )+(-24)× +(-24)×(- )
1
3
3
4
1
6
5
8
①(- )×(8-1 -4)
3
4
1
3
②(-11)×(- )+(-11)×2 +(-11)×(- )
2
5
3
5
1
5
3.计算:
答案 :
①-2;
②-22
典例精练
例4.如何计算 71 ×(–9)?
提示:把 拆分成 .
解:原式=
=
=
=
典例精析
典例精练
1.已知两个有理数a,b,如果ab<0且a+b>0,那么( )
A.a>0,b>0 B.a<0,b>0
C.a、b同号 D.a、b异号,且正数的绝对值较大
分析:∵ab<0,∴a,b异号,
∵a+b>0,
∴正数的绝对值较大.
D
中考链接
利用运算律有时能进行简便运算.
例1 98×12=(100-2) ×12=1200-24=1176
例2 (-16) ×223+17×233=(-16+17) ×233=233
2.
请你参考黑板中老师的讲解,用运算律简便计算:
(1)999×(-15);
(2) .
分析:(1)将式子变形为(1000-1)×(-15),再根据乘法分配
律计算即可求解;
(2)根据乘法分配律计算即可求解.
解:(1)999×(-15)
=(1000-1) ×(-15)
=1000×(-15)+15
= -15000+15
= -14985
(2)
=
=
999×11845+999×(?15)?999×1835
?
999×(11845?15?1835)
?
999×100
?
= 99900
B
D
当堂练习
3.算式-25×14+18×14-39×(-14)
=(-25+18+39)×14是逆用了( )
A.加法交换律 B.乘法交换律
C.乘法结合律 D.乘法分配律
D
C
-2
0或2
A
8.a、b、c为非零有理数,它们的积必为正数的是( )
A.a>0,b、c同号 B.b>0,a、c异号
C.c>0,a、b异号 D.a、b、c同号
9.已知abc>0,a>0,ac>0,则下列结论正确的是( )
A.b<0,c<0 B.b>0,c<0
C.b<0,c>0 D.b>0,c>0
A
D
-1
1
(3)0.25×320×0.125;
解:原式=0.25×(4×80)×0.125=(0.25×4)×(80×0.125)=1×10=10.
能力提升
两个数相乘,交换两个因数的位置,积相等.
ab=ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
(ab)c = a(bc)
1.乘法交换律:
2.乘法结合律:
数的范围已扩充到有理数.
注意:用字母表示乘数时,“×”号可以写成“·”或省略, 如a×b可以写成a·b或ab.
课堂小结
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
3.乘法分配律:
a(b+c)
ab+ac
=
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,也可先把其中的几个数相乘.
根据分配律可以推出:
一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.
a(b+c+d )=ab+ac+ad
及运用(第2课时)
第 1 章 有 理 数
七年级上册数学人教版
目录
有理数乘法运算律
01
乘法运算律应用
02
学习目标
1.掌握乘法的分配律,并能灵活的运用.(难点)
2.掌握有理数乘法的运算律,并利用运算律简化乘法运算.(重点)
问题引入
1.有理数的乘法法则是什么?
3.小学时候大家学过乘法的哪些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和零相乘,都得0
乘法交换律、乘法结合律、乘法分配律
2.如何进行多个有理数的乘法运算?
(1)定号(奇负偶正) (2)算值(积的绝对值)
问题1 观察下列各式,它们的积是正的还是负的?
,
,
,
思考:几个不是0
的数相乘,积的符号
.
组卷组卷网
网
归纳:
几个不是0的数相乘,负因数的个数是______
时,积是正数;负因数的个数是_________时,积
是负数.
偶数
奇数
典例精析
几个不等于零的数相乘,积的正负号由负因数的个数决定,当负因数的个数为奇数时,积为负;当负因数的个数为偶数时,积为正.
几个不等于零的数相乘,首先确定积的正负号,然后把绝对值相乘。
归纳总结
几个数相乘,如果其中有因数为0,积等于____.
问题2
你能看出下式的结果吗?如果能,请说明理由学科网
0
1.有理数乘法运算律
问题3 计算下列各题,并比较它们的结果,
你有什么发现?请再举几个例子验证你的发现.
5×(-6)=? (-6)×5=?
你发现了什么规律?
①.两个数相乘,交换两个因数的位置,积不变.
乘法交换律:ab=ba.
a×b可以写成a·b,还可以写成ab.
[3×(-4)]×(-5)=?
3×[(-4)×(-5)]=?
你又能发现什么规律?
②.三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变.
乘法结合律:(ab)c=a(bc).
5×[3+(-7)]=
5×3+5×(-7) =
5×(-4) =-20
15+(-35)=-20
③一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加. Z```xxk
乘法分配律:a(b+c)=ab+ac.
2. 乘法运算律应用
典例精析
例2 计算:(-85)×(-25)×(-4)
解:原式=(-85)×[(-25)×(-4)]
=(-85)×100
=-8500
1.计算: (-8)×(-12)×(-0.125)×(- )×(-0.1)
1
3
解:原式=-8×(-0.125) ×(-12) ×(- ) ×(-0.1)
=[-8×(-0.125)] ×[(-12) ×(- )] ×(-0.1)
=1×4×(-0.1)
=-0.4
典例精练
( + - )×12
例3 用两种方法计算
1
2
1
6
1
4
解法1:
( + - )×12
3
12
2
12
6
12
原式=
1
12
=- ×12
=-1
解法2:
原式=
×12 + ×12- ×12
1
4
1
6
1
2
=3+2-6
=-1
典例精析
解法有错吗?错在哪里?
? ? ?
__ __ __
(-24)×( - + - )
5
8
1
6
3
4
1
3
解:
原式=
-24× -24× +24× -24×
5
8
1
6
3
4
1
3
2.计算:
=-8-18+4-15
=-41+4
=-37
观察与思考
正确解法:
特别提醒:
1.不要漏掉符号,
2.不要漏乘.
_____ ______ ______ ______
(-24)×( - + - )
5
8
1
6
3
4
1
3
=-8+18-4+15
=-12+33
=21
=(-24)× +(-24)×(- )+(-24)× +(-24)×(- )
1
3
3
4
1
6
5
8
①(- )×(8-1 -4)
3
4
1
3
②(-11)×(- )+(-11)×2 +(-11)×(- )
2
5
3
5
1
5
3.计算:
答案 :
①-2;
②-22
典例精练
例4.如何计算 71 ×(–9)?
提示:把 拆分成 .
解:原式=
=
=
=
典例精析
典例精练
1.已知两个有理数a,b,如果ab<0且a+b>0,那么( )
A.a>0,b>0 B.a<0,b>0
C.a、b同号 D.a、b异号,且正数的绝对值较大
分析:∵ab<0,∴a,b异号,
∵a+b>0,
∴正数的绝对值较大.
D
中考链接
利用运算律有时能进行简便运算.
例1 98×12=(100-2) ×12=1200-24=1176
例2 (-16) ×223+17×233=(-16+17) ×233=233
2.
请你参考黑板中老师的讲解,用运算律简便计算:
(1)999×(-15);
(2) .
分析:(1)将式子变形为(1000-1)×(-15),再根据乘法分配
律计算即可求解;
(2)根据乘法分配律计算即可求解.
解:(1)999×(-15)
=(1000-1) ×(-15)
=1000×(-15)+15
= -15000+15
= -14985
(2)
=
=
999×11845+999×(?15)?999×1835
?
999×(11845?15?1835)
?
999×100
?
= 99900
B
D
当堂练习
3.算式-25×14+18×14-39×(-14)
=(-25+18+39)×14是逆用了( )
A.加法交换律 B.乘法交换律
C.乘法结合律 D.乘法分配律
D
C
-2
0或2
A
8.a、b、c为非零有理数,它们的积必为正数的是( )
A.a>0,b、c同号 B.b>0,a、c异号
C.c>0,a、b异号 D.a、b、c同号
9.已知abc>0,a>0,ac>0,则下列结论正确的是( )
A.b<0,c<0 B.b>0,c<0
C.b<0,c>0 D.b>0,c>0
A
D
-1
1
(3)0.25×320×0.125;
解:原式=0.25×(4×80)×0.125=(0.25×4)×(80×0.125)=1×10=10.
能力提升
两个数相乘,交换两个因数的位置,积相等.
ab=ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
(ab)c = a(bc)
1.乘法交换律:
2.乘法结合律:
数的范围已扩充到有理数.
注意:用字母表示乘数时,“×”号可以写成“·”或省略, 如a×b可以写成a·b或ab.
课堂小结
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
3.乘法分配律:
a(b+c)
ab+ac
=
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,也可先把其中的几个数相乘.
根据分配律可以推出:
一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.
a(b+c+d )=ab+ac+ad
