2.2 去括号(第2课时) 课件(共30张PPT)
文档属性
| 名称 | 2.2 去括号(第2课时) 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 631.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 11:47:03 | ||
图片预览






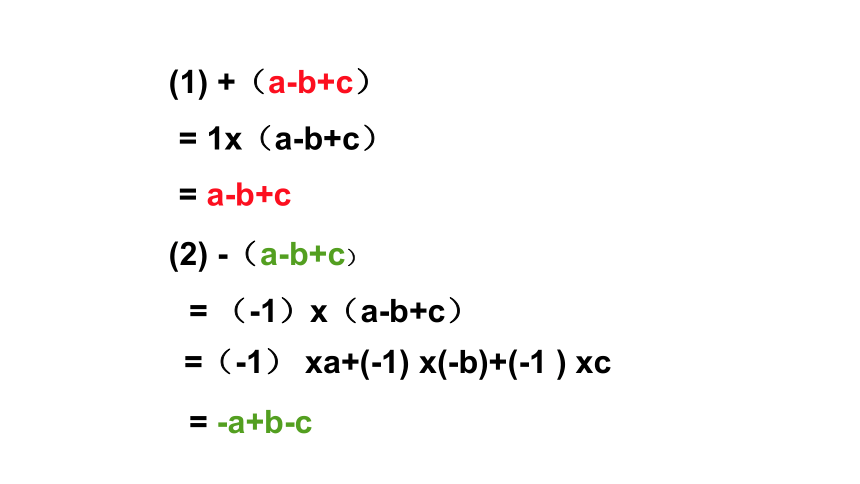





文档简介
(共30张PPT)
2.2 去括号(第2课时)
第 2 章整式的加减
七年级上册数学人教版
目录
去括号化简
01
去括号化简应用
03
去括号化简求值
02
学习目标
1.能运用运算律探究去括号法则.(重点)
2.会利用去括号法则将整式化简.(难点)
=(-1)x(3-7)
-(+5)=
+(+5)=
-(-7)=
+(-7)=
- 5
+5
+7
-7
1. 化简
=(-1) x 3+(-1) x(-7)
= - 3 + 7
= 1 x 3+1 x (-7)
= 3 - 7
2. 去括号
① -(3- 7)
② +(3- 7)
+3 与-7的 和
=(+1) x(3-7)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
(1)4( a+b)
(2)5(a-b)
=4(+a ) +4( +b )
=5(+a)+5(-b)
(3)-2(a+b)
(4)-3(a-b)
=(-2a)+(-2b)
=(-3a)+(-3)(-b)
用分配律计算
根据分配律,你能为下面的式子去括号吗?
(1) +(a-b)
(2) -(a-b)
= 1x(a-b)
= (-1)x(a-b)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
= a-b
= -a+b
=(-1) xa+(-1) x(-b)
(1) +(a-b+c)
(2) -(a-b+c)
= 1x(a-b+c)
= (-1)x(a-b+c)
= a-b+c
= -a+b-c
=(-1) xa+(-1) x(-b)+(-1 ) xc
1. 去括号化简
合作探究
利用乘法分配律计算:你有几种方法?
-7(3y-4)=?
用类似方法计算下列各式:
(1)2(x+8)=
(2)-3(3x+4)=
(3)-7(7y-5)=
2x+16
-9x-12
-49y+35
试一试
(1)3(x+8)=3x+8
(2)-3(x-8)=-3x-24
(4)-2(6-x)=-12+2x
(3)4(-3-2x)=-12+8x
错
3x+3×8
错因:分配律,漏乘3.
错
-3x+24
错因:括号前面是负数,去掉负号和括号后每一项都变号.
对
错
错因:括号前面是正数,去掉正号和括号后每一项都不变号.
-12-8x
判一判
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
顺口溜:
去括号,看符号:
是“+”号,不变号;
是“-”号,全变号;
原来的符号和括号都扔掉.
去括号时符号变化的规律:
归纳总结
议一议
讨论比较
+(x-3)与 -(x-3)的区别?
+(x-3)与-(x-3)可以分别看作1与-1分别乘(x-3)
注意:准确理解去括号的规律,去括号时括号内的每一项的符号都要考虑,做到要变都变,要不变,则都不变;另外,括号内原有几项去掉括号后仍有几项.
例1:化简下列各式:
(1)8a+2b+(5a-b); (2)(5a-3b)-3(a2-2b)
解析:根据去括号的法则去括号后再合并同类项.
解:(1)原式=8a+2b+5a-b
=13a+b
(2)原式=5a-3b-(3a2-6b)
=5a-3b-3a2+6b
=-3a2+5a+3b
(3)(2x2+x)-[4x2-(3x2-x)].[
解:原式 =2x2+x-(4x2-3x2+x)
=2x2+x-(x2+x)
=2x2+x-x2-x
=2x2.
要点归纳:1.当括号前面有数字因数时,可应用乘法分配律将这个数字因数乘以括号内的每一项,切勿漏乘.
2.当含有多重括号时,可以由内向外逐层去括号,也可以由外向内逐层去括号.每去掉一层括号,若有同类项可随时合并,这样可使下一步运算简化,减少差错.
针对训练
化简:
(1)3(a2-4a+3)-5(5a2-a+2);
(2)3(x2-5xy)-4(x2+2xy-y2)-5(y2-3xy);
(3)abc-[2ab-(3abc-ab)+4abc]
解:(1)原式=3a2-12a+9-25a2+5a-10
=-22a2-7a-1;
(2)原式=3x2-15xy-4x2-8xy+4y2-5y2+15xy
=-x2-8xy-y2;
(3)原式=abc-(2ab-3abc+ab+4abc)
=abc-3ab-abc=-3ab.
2. 去括号化简求值
解析:将原式化简,观察化简后的结果.
先化简,再求值:已知x=-4,y= ,求5xy2-[3xy2-(4xy2-2x2y)]+2x2y-xy2.
归纳总结:在化简时要注意去括号时是否变号;在代入时若所给的值是负数、分数、有乘方运算的,代入时要添上括号.
解:原式=5xy2-(-xy2+2x2y)+2x2y-xy2
=5xy2.
当x=-4,y=1/2时,
原式=5×(-4)×(1/2)2=-5.
针对训练
3. 去括号化简应用
例3:两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,
两船在静水中的速度都是50 km/h,水流速度是a km/h.
(1)2h后两船相距多远?
(2)2h后甲船比乙船多航行多少千米?
解析:(1)求甲、乙两船航行的路程和;
(2)求甲、乙两船航行的路程的差.
解:顺水航速=船速+水速=(50+a)km/h,
逆水航速=船速-水速=(50-a)km/h
(1)2h后两船相距(单位:km)
2(50+a)+2(50-a)=100+2a+100-2a=200.;
(2)2h后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a)=100+2a-100+2a=4a.
飞机的无风航速为x千米/时,风速为20千米/时,飞机顺
飞行4小时的行程是多少?飞机逆风飞行3小时的行程是多
少?两个行程相差多少?
解:顺风航速=无风航速___风速=_________________
逆风航速=无风航速___风速=_________________
飞机顺风飞行4小时的行程是
飞机逆风飞行3小时的行程是
两个行程相差
+
4(x+20)=(4x+80)(千米)
–
(x+20)(千米)
(x– 20)(千米)
3(x–20)=(3x–60)(千米)
(4x+80)–(3x–60)= 4x+80–3x+60=x+140(千米)
针对训练
1. 已知a2+2a=1,则3(a2+2a)+2的值为 .
解析:∵a2+2a=1,
∴3(a2+2a)+2=3×1+2=5.
5
中考链接
解析:A. x=3、y=3时,输出结果为32+2×3=15;
B. x= –4、y= –2时,输出结果为(–4)2–2×(–2)=20;
C. x=2、y=4时,输出结果为22+2×4=12;
D. x=4、y=2时,输出结果为42+2×2=20.
2. 按如图所示的运算程序,能使输出的结果为12的是( )
A.x=3,y=3 B.x= –4,y= –2 C.x=2,y=4 D.x=4,y=2
C
x2-2y
x2+2y
中考链接
当堂检测
1.下列运算正确的是 ( )
A.-2(3x-1)=-6x-1 B.-2(3x-1)=-6x+1
C.-2(3x-1)=-6x-2 D.-2(3x-1)=-6x+2
2.已知x-( )=x-y-z+a,则括号中的多项式应是 ( )
A.y-z+a B.y+z-a
C.y+z+a D.-y+z-a
3.去括号:a-(2b-3c)= ;
2(a-b)-3(c-d)= .
D
B
a-2b+3c
2a-2b-3c+3d
4.一个长方形的周长为4m,一边长为m-n,则另一边长为( )
A.3m+n B.2m+2n C.m+n D.m+3n
5.化简:2(a+1)-a= .
C
a+2
6.化简-2a+(2a-1)的结果是 ( )
A.-4a-1 B.4a-1 C.1 D.-1
7.与a+b-c互为相反数的是 ( )
A.c-a-b B. a-b+c
C.-a+b+c D.-a-b-c
D
A
8.下列各式去括号:
①x+(-y+z)=x-y+z;②x-(-y-z)=x-y-z;
③x+(-y-z)=x+y+z;④x-(-y+z)=x+y-z.
其中正确的是(填序号) .
9.化简:3x2-2x+1-2(x-1)= .
①④
3x2-4x+3
10.化简:
(1)4a-(2b-3c); (2)m+2(3m-2);
解:原式=4a-2b+3c
解:原式=m+6m-4
=7m-4
(3)-(x-3)-3 ( x-3z); (4)3 ( 2x2-y2)-2 ( 3y2-2x2).
解:原式=-x+3-3x+9z
=-4x+9z+3
解:原式=6x2-3y2-6y2+4x2
=(6+4)x2+(-3-6)y2
=10x2-9y2
去括号法则
括号前是“+”
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
括号前是“–”
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
课堂小结
2.2 去括号(第2课时)
第 2 章整式的加减
七年级上册数学人教版
目录
去括号化简
01
去括号化简应用
03
去括号化简求值
02
学习目标
1.能运用运算律探究去括号法则.(重点)
2.会利用去括号法则将整式化简.(难点)
=(-1)x(3-7)
-(+5)=
+(+5)=
-(-7)=
+(-7)=
- 5
+5
+7
-7
1. 化简
=(-1) x 3+(-1) x(-7)
= - 3 + 7
= 1 x 3+1 x (-7)
= 3 - 7
2. 去括号
① -(3- 7)
② +(3- 7)
+3 与-7的 和
=(+1) x(3-7)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
(1)4( a+b)
(2)5(a-b)
=4(+a ) +4( +b )
=5(+a)+5(-b)
(3)-2(a+b)
(4)-3(a-b)
=(-2a)+(-2b)
=(-3a)+(-3)(-b)
用分配律计算
根据分配律,你能为下面的式子去括号吗?
(1) +(a-b)
(2) -(a-b)
= 1x(a-b)
= (-1)x(a-b)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
= a-b
= -a+b
=(-1) xa+(-1) x(-b)
(1) +(a-b+c)
(2) -(a-b+c)
= 1x(a-b+c)
= (-1)x(a-b+c)
= a-b+c
= -a+b-c
=(-1) xa+(-1) x(-b)+(-1 ) xc
1. 去括号化简
合作探究
利用乘法分配律计算:你有几种方法?
-7(3y-4)=?
用类似方法计算下列各式:
(1)2(x+8)=
(2)-3(3x+4)=
(3)-7(7y-5)=
2x+16
-9x-12
-49y+35
试一试
(1)3(x+8)=3x+8
(2)-3(x-8)=-3x-24
(4)-2(6-x)=-12+2x
(3)4(-3-2x)=-12+8x
错
3x+3×8
错因:分配律,漏乘3.
错
-3x+24
错因:括号前面是负数,去掉负号和括号后每一项都变号.
对
错
错因:括号前面是正数,去掉正号和括号后每一项都不变号.
-12-8x
判一判
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
顺口溜:
去括号,看符号:
是“+”号,不变号;
是“-”号,全变号;
原来的符号和括号都扔掉.
去括号时符号变化的规律:
归纳总结
议一议
讨论比较
+(x-3)与 -(x-3)的区别?
+(x-3)与-(x-3)可以分别看作1与-1分别乘(x-3)
注意:准确理解去括号的规律,去括号时括号内的每一项的符号都要考虑,做到要变都变,要不变,则都不变;另外,括号内原有几项去掉括号后仍有几项.
例1:化简下列各式:
(1)8a+2b+(5a-b); (2)(5a-3b)-3(a2-2b)
解析:根据去括号的法则去括号后再合并同类项.
解:(1)原式=8a+2b+5a-b
=13a+b
(2)原式=5a-3b-(3a2-6b)
=5a-3b-3a2+6b
=-3a2+5a+3b
(3)(2x2+x)-[4x2-(3x2-x)].[
解:原式 =2x2+x-(4x2-3x2+x)
=2x2+x-(x2+x)
=2x2+x-x2-x
=2x2.
要点归纳:1.当括号前面有数字因数时,可应用乘法分配律将这个数字因数乘以括号内的每一项,切勿漏乘.
2.当含有多重括号时,可以由内向外逐层去括号,也可以由外向内逐层去括号.每去掉一层括号,若有同类项可随时合并,这样可使下一步运算简化,减少差错.
针对训练
化简:
(1)3(a2-4a+3)-5(5a2-a+2);
(2)3(x2-5xy)-4(x2+2xy-y2)-5(y2-3xy);
(3)abc-[2ab-(3abc-ab)+4abc]
解:(1)原式=3a2-12a+9-25a2+5a-10
=-22a2-7a-1;
(2)原式=3x2-15xy-4x2-8xy+4y2-5y2+15xy
=-x2-8xy-y2;
(3)原式=abc-(2ab-3abc+ab+4abc)
=abc-3ab-abc=-3ab.
2. 去括号化简求值
解析:将原式化简,观察化简后的结果.
先化简,再求值:已知x=-4,y= ,求5xy2-[3xy2-(4xy2-2x2y)]+2x2y-xy2.
归纳总结:在化简时要注意去括号时是否变号;在代入时若所给的值是负数、分数、有乘方运算的,代入时要添上括号.
解:原式=5xy2-(-xy2+2x2y)+2x2y-xy2
=5xy2.
当x=-4,y=1/2时,
原式=5×(-4)×(1/2)2=-5.
针对训练
3. 去括号化简应用
例3:两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,
两船在静水中的速度都是50 km/h,水流速度是a km/h.
(1)2h后两船相距多远?
(2)2h后甲船比乙船多航行多少千米?
解析:(1)求甲、乙两船航行的路程和;
(2)求甲、乙两船航行的路程的差.
解:顺水航速=船速+水速=(50+a)km/h,
逆水航速=船速-水速=(50-a)km/h
(1)2h后两船相距(单位:km)
2(50+a)+2(50-a)=100+2a+100-2a=200.;
(2)2h后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a)=100+2a-100+2a=4a.
飞机的无风航速为x千米/时,风速为20千米/时,飞机顺
飞行4小时的行程是多少?飞机逆风飞行3小时的行程是多
少?两个行程相差多少?
解:顺风航速=无风航速___风速=_________________
逆风航速=无风航速___风速=_________________
飞机顺风飞行4小时的行程是
飞机逆风飞行3小时的行程是
两个行程相差
+
4(x+20)=(4x+80)(千米)
–
(x+20)(千米)
(x– 20)(千米)
3(x–20)=(3x–60)(千米)
(4x+80)–(3x–60)= 4x+80–3x+60=x+140(千米)
针对训练
1. 已知a2+2a=1,则3(a2+2a)+2的值为 .
解析:∵a2+2a=1,
∴3(a2+2a)+2=3×1+2=5.
5
中考链接
解析:A. x=3、y=3时,输出结果为32+2×3=15;
B. x= –4、y= –2时,输出结果为(–4)2–2×(–2)=20;
C. x=2、y=4时,输出结果为22+2×4=12;
D. x=4、y=2时,输出结果为42+2×2=20.
2. 按如图所示的运算程序,能使输出的结果为12的是( )
A.x=3,y=3 B.x= –4,y= –2 C.x=2,y=4 D.x=4,y=2
C
x2-2y
x2+2y
中考链接
当堂检测
1.下列运算正确的是 ( )
A.-2(3x-1)=-6x-1 B.-2(3x-1)=-6x+1
C.-2(3x-1)=-6x-2 D.-2(3x-1)=-6x+2
2.已知x-( )=x-y-z+a,则括号中的多项式应是 ( )
A.y-z+a B.y+z-a
C.y+z+a D.-y+z-a
3.去括号:a-(2b-3c)= ;
2(a-b)-3(c-d)= .
D
B
a-2b+3c
2a-2b-3c+3d
4.一个长方形的周长为4m,一边长为m-n,则另一边长为( )
A.3m+n B.2m+2n C.m+n D.m+3n
5.化简:2(a+1)-a= .
C
a+2
6.化简-2a+(2a-1)的结果是 ( )
A.-4a-1 B.4a-1 C.1 D.-1
7.与a+b-c互为相反数的是 ( )
A.c-a-b B. a-b+c
C.-a+b+c D.-a-b-c
D
A
8.下列各式去括号:
①x+(-y+z)=x-y+z;②x-(-y-z)=x-y-z;
③x+(-y-z)=x+y+z;④x-(-y+z)=x+y-z.
其中正确的是(填序号) .
9.化简:3x2-2x+1-2(x-1)= .
①④
3x2-4x+3
10.化简:
(1)4a-(2b-3c); (2)m+2(3m-2);
解:原式=4a-2b+3c
解:原式=m+6m-4
=7m-4
(3)-(x-3)-3 ( x-3z); (4)3 ( 2x2-y2)-2 ( 3y2-2x2).
解:原式=-x+3-3x+9z
=-4x+9z+3
解:原式=6x2-3y2-6y2+4x2
=(6+4)x2+(-3-6)y2
=10x2-9y2
去括号法则
括号前是“+”
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
括号前是“–”
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
课堂小结
