2022-2023学年人教版八年级上册数学13.1.2.2 线段垂直平分线的有关作图 练习(word、含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级上册数学13.1.2.2 线段垂直平分线的有关作图 练习(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 104.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 18:31:25 | ||
图片预览

文档简介
13.1.2.2 线段垂直平分线的有关作图
一.选择题
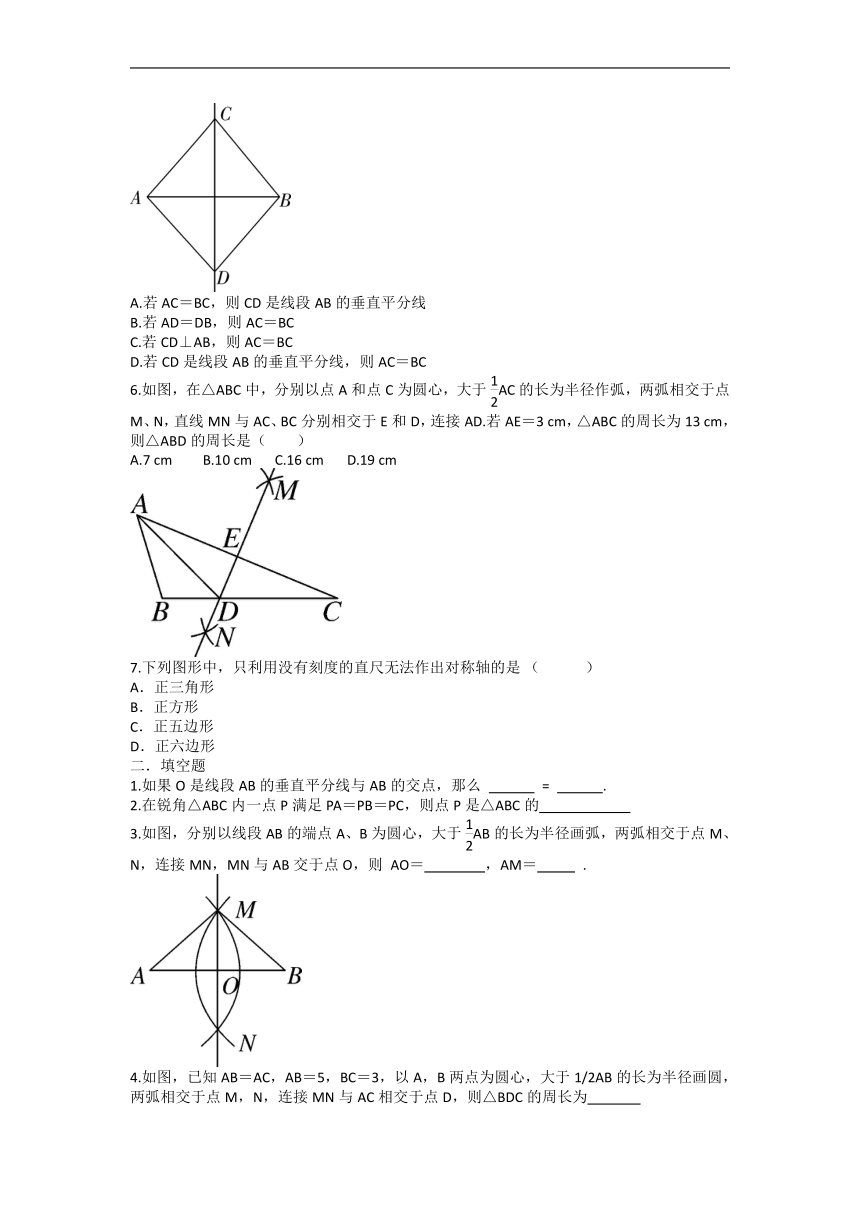
1.如图,直线PO与AB交于点O,且PA=PB,则下列结论中正确的是( )
A.PO⊥AB
B.PO是线段AB的垂直平分线
C.AO=BO
D.点P在线段AB的垂直平分线上
2.如图所示的尺规作图是作( )
A.线段的垂直平分线
B.一个半径为定值的圆
C.角的平分线
D.一个角等于已知角
3. 在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三边垂直平分线的交点
4.如图,在△ABC中,AC=BC,AB=16,用尺规作图作出CF,交AB于点G.若CG=4,则△ACG的面积为( )
A.64 B.32 C.16 D.8
5. 如图,下列说法正确的是( )
A.若AC=BC,则CD是线段AB的垂直平分线
B.若AD=DB,则AC=BC
C.若CD⊥AB,则AC=BC
D.若CD是线段AB的垂直平分线,则AC=BC
6.如图,在△ABC中,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于点M、N,直线MN与AC、BC分别相交于E和D,连接AD.若AE=3 cm,△ABC的周长为13 cm,则△ABD的周长是( )
A.7 cm B.10 cm C.16 cm D.19 cm
7.下列图形中,只利用没有刻度的直尺无法作出对称轴的是 ( )
A.正三角形
B.正方形
C.正五边形
D.正六边形
填空题
1.如果O是线段AB的垂直平分线与AB的交点,那么 = .
2.在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC的
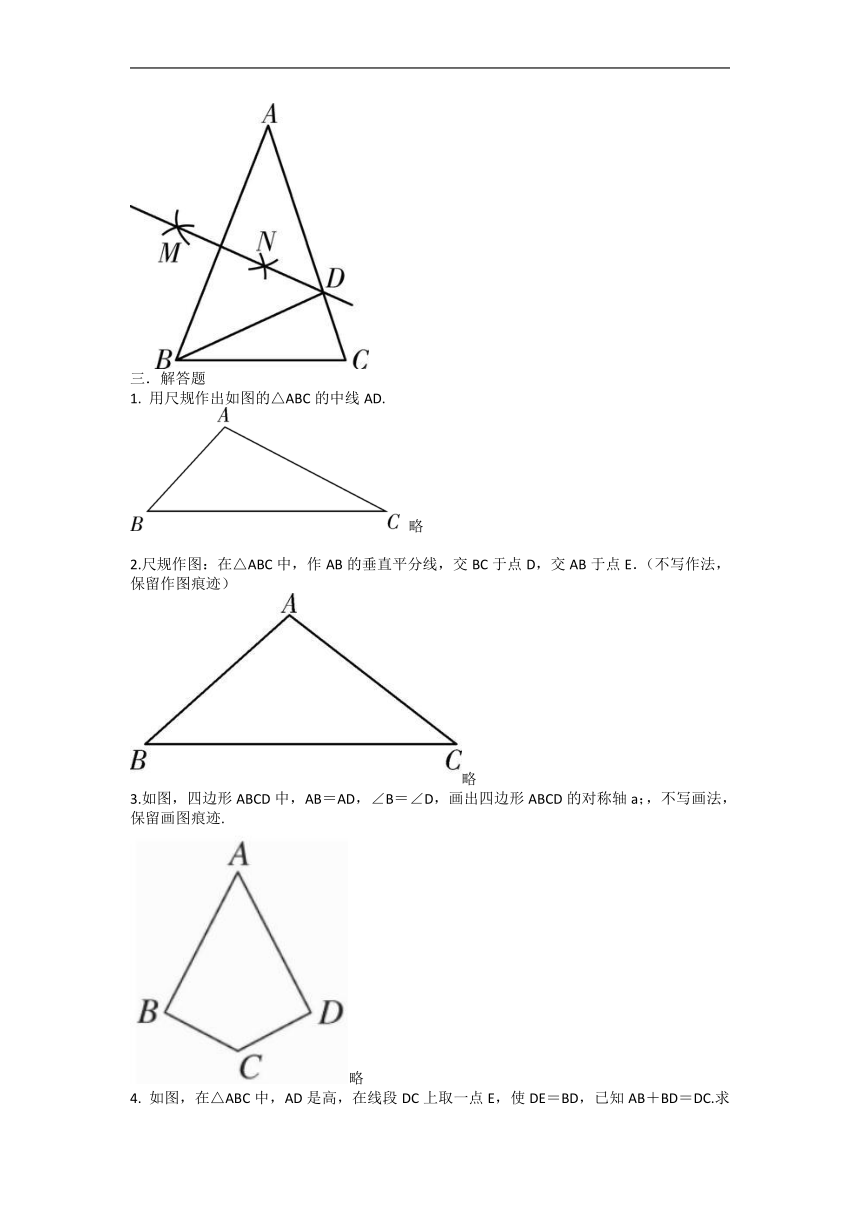
3.如图,分别以线段AB的端点A、B为圆心,大于AB的长为半径画弧,两弧相交于点M、N,连接MN,MN与AB交于点O,则 AO= ,AM= .
4.如图,已知AB=AC,AB=5,BC=3,以A,B两点为圆心,大于1/2AB的长为半径画圆,两弧相交于点M,N,连接MN与AC相交于点D,则△BDC的周长为
解答题
1. 用尺规作出如图的△ABC的中线AD.
略
2.尺规作图:在△ABC中,作AB的垂直平分线,交BC于点D,交AB于点E.(不写作法,保留作图痕迹)
略
3.如图,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴a;,不写画法,保留画图痕迹.
略
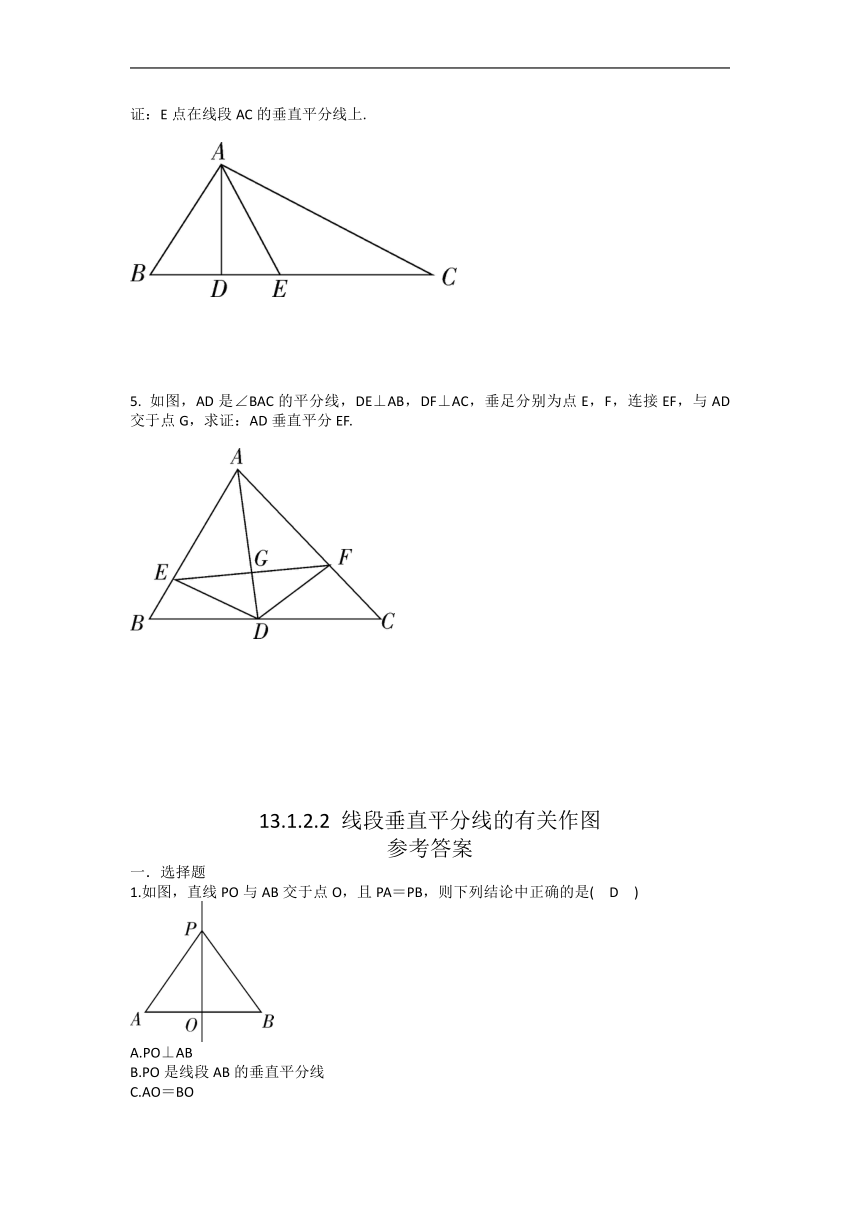
4. 如图,在△ABC中,AD是高,在线段DC上取一点E,使DE=BD,已知AB+BD=DC.求证:E点在线段AC的垂直平分线上.
5. 如图,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为点E,F,连接EF,与AD交于点G,求证:AD垂直平分EF.
13.1.2.2 线段垂直平分线的有关作图
参考答案
一.选择题
1.如图,直线PO与AB交于点O,且PA=PB,则下列结论中正确的是( D )
A.PO⊥AB
B.PO是线段AB的垂直平分线
C.AO=BO
D.点P在线段AB的垂直平分线上
2.如图所示的尺规作图是作( A )
A.线段的垂直平分线
B.一个半径为定值的圆
C.角的平分线
D.一个角等于已知角
3. 在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC( D )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三边垂直平分线的交点
4.如图,在△ABC中,AC=BC,AB=16,用尺规作图作出CF,交AB于点G.若CG=4,则△ACG的面积为( C )
A.64 B.32 C.16 D.8
5. 如图,下列说法正确的是( D )
A.若AC=BC,则CD是线段AB的垂直平分线
B.若AD=DB,则AC=BC
C.若CD⊥AB,则AC=BC
D.若CD是线段AB的垂直平分线,则AC=BC
6.如图,在△ABC中,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于点M、N,直线MN与AC、BC分别相交于E和D,连接AD.若AE=3 cm,△ABC的周长为13 cm,则△ABD的周长是( A )
A.7 cm B.10 cm C.16 cm D.19 cm
7.下列图形中,只利用没有刻度的直尺无法作出对称轴的是 ( A )
A.正三角形
B.正方形
C.正五边形
D.正六边形
填空题
1.如果O是线段AB的垂直平分线与AB的交点,那么 OA = OB .
2.在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC的 三边垂直平分线的交点
3.如图,分别以线段AB的端点A、B为圆心,大于AB的长为半径画弧,两弧相交于点M、N,连接MN,MN与AB交于点O,则 AO=BO(或AB) ,AM= BM .
4.如图,已知AB=AC,AB=5,BC=3,以A,B两点为圆心,大于1/2AB的长为半径画圆,两弧相交于点M,N,连接MN与AC相交于点D,则△BDC的周长为 8
解答题
1. 用尺规作出如图的△ABC的中线AD.
2.尺规作图:在△ABC中,作AB的垂直平分线,交BC于点D,交AB于点E.(不写作法,保留作图痕迹)
3.如图,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴a;,不写画法,保留画图痕迹.
4. 如图,在△ABC中,AD是高,在线段DC上取一点E,使DE=BD,已知AB+BD=DC.求证:E点在线段AC的垂直平分线上.
证明:∵AD是高,∴AD⊥BC.
又∵BD=DE,∴AD所在的直线是线段BE的垂直平分线.
∴AB=AE.∴AB+BD=AE+DE.
又∵AB+BD=DC,∴DC=AE+DE.
∴DE+EC=AE+DE.∴EC=AE.∴点E在线段AC的垂直平分线上.
5. 如图,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为点E,F,连接EF,与AD交于点G,求证:AD垂直平分EF.
证明:∵AD是∠BAC的平分线, DE⊥AB,DF⊥AC,
∴DE=DF,
∠AED=∠AFD=90°.
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL).∴AE=AF.
又∵DE=DF,∴AD垂直平分EF.
一.选择题
1.如图,直线PO与AB交于点O,且PA=PB,则下列结论中正确的是( )
A.PO⊥AB
B.PO是线段AB的垂直平分线
C.AO=BO
D.点P在线段AB的垂直平分线上
2.如图所示的尺规作图是作( )
A.线段的垂直平分线
B.一个半径为定值的圆
C.角的平分线
D.一个角等于已知角
3. 在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三边垂直平分线的交点
4.如图,在△ABC中,AC=BC,AB=16,用尺规作图作出CF,交AB于点G.若CG=4,则△ACG的面积为( )
A.64 B.32 C.16 D.8
5. 如图,下列说法正确的是( )
A.若AC=BC,则CD是线段AB的垂直平分线
B.若AD=DB,则AC=BC
C.若CD⊥AB,则AC=BC
D.若CD是线段AB的垂直平分线,则AC=BC
6.如图,在△ABC中,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于点M、N,直线MN与AC、BC分别相交于E和D,连接AD.若AE=3 cm,△ABC的周长为13 cm,则△ABD的周长是( )
A.7 cm B.10 cm C.16 cm D.19 cm
7.下列图形中,只利用没有刻度的直尺无法作出对称轴的是 ( )
A.正三角形
B.正方形
C.正五边形
D.正六边形
填空题
1.如果O是线段AB的垂直平分线与AB的交点,那么 = .
2.在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC的
3.如图,分别以线段AB的端点A、B为圆心,大于AB的长为半径画弧,两弧相交于点M、N,连接MN,MN与AB交于点O,则 AO= ,AM= .
4.如图,已知AB=AC,AB=5,BC=3,以A,B两点为圆心,大于1/2AB的长为半径画圆,两弧相交于点M,N,连接MN与AC相交于点D,则△BDC的周长为
解答题
1. 用尺规作出如图的△ABC的中线AD.
略
2.尺规作图:在△ABC中,作AB的垂直平分线,交BC于点D,交AB于点E.(不写作法,保留作图痕迹)
略
3.如图,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴a;,不写画法,保留画图痕迹.
略
4. 如图,在△ABC中,AD是高,在线段DC上取一点E,使DE=BD,已知AB+BD=DC.求证:E点在线段AC的垂直平分线上.
5. 如图,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为点E,F,连接EF,与AD交于点G,求证:AD垂直平分EF.
13.1.2.2 线段垂直平分线的有关作图
参考答案
一.选择题
1.如图,直线PO与AB交于点O,且PA=PB,则下列结论中正确的是( D )
A.PO⊥AB
B.PO是线段AB的垂直平分线
C.AO=BO
D.点P在线段AB的垂直平分线上
2.如图所示的尺规作图是作( A )
A.线段的垂直平分线
B.一个半径为定值的圆
C.角的平分线
D.一个角等于已知角
3. 在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC( D )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三边垂直平分线的交点
4.如图,在△ABC中,AC=BC,AB=16,用尺规作图作出CF,交AB于点G.若CG=4,则△ACG的面积为( C )
A.64 B.32 C.16 D.8
5. 如图,下列说法正确的是( D )
A.若AC=BC,则CD是线段AB的垂直平分线
B.若AD=DB,则AC=BC
C.若CD⊥AB,则AC=BC
D.若CD是线段AB的垂直平分线,则AC=BC
6.如图,在△ABC中,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于点M、N,直线MN与AC、BC分别相交于E和D,连接AD.若AE=3 cm,△ABC的周长为13 cm,则△ABD的周长是( A )
A.7 cm B.10 cm C.16 cm D.19 cm
7.下列图形中,只利用没有刻度的直尺无法作出对称轴的是 ( A )
A.正三角形
B.正方形
C.正五边形
D.正六边形
填空题
1.如果O是线段AB的垂直平分线与AB的交点,那么 OA = OB .
2.在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC的 三边垂直平分线的交点
3.如图,分别以线段AB的端点A、B为圆心,大于AB的长为半径画弧,两弧相交于点M、N,连接MN,MN与AB交于点O,则 AO=BO(或AB) ,AM= BM .
4.如图,已知AB=AC,AB=5,BC=3,以A,B两点为圆心,大于1/2AB的长为半径画圆,两弧相交于点M,N,连接MN与AC相交于点D,则△BDC的周长为 8
解答题
1. 用尺规作出如图的△ABC的中线AD.
2.尺规作图:在△ABC中,作AB的垂直平分线,交BC于点D,交AB于点E.(不写作法,保留作图痕迹)
3.如图,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴a;,不写画法,保留画图痕迹.
4. 如图,在△ABC中,AD是高,在线段DC上取一点E,使DE=BD,已知AB+BD=DC.求证:E点在线段AC的垂直平分线上.
证明:∵AD是高,∴AD⊥BC.
又∵BD=DE,∴AD所在的直线是线段BE的垂直平分线.
∴AB=AE.∴AB+BD=AE+DE.
又∵AB+BD=DC,∴DC=AE+DE.
∴DE+EC=AE+DE.∴EC=AE.∴点E在线段AC的垂直平分线上.
5. 如图,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为点E,F,连接EF,与AD交于点G,求证:AD垂直平分EF.
证明:∵AD是∠BAC的平分线, DE⊥AB,DF⊥AC,
∴DE=DF,
∠AED=∠AFD=90°.
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL).∴AE=AF.
又∵DE=DF,∴AD垂直平分EF.
