2022-2023学年人教版数学八年级上册11.2与三角形有关的角 同步精练(word、含答案)
文档属性
| 名称 | 2022-2023学年人教版数学八年级上册11.2与三角形有关的角 同步精练(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 342.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 18:34:00 | ||
图片预览

文档简介
11.2与三角形有关的角 同步精练
一、单选题
1.如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )
A.90° B.95° C.100° D.150°
2.如图,直线,点C为直线MN上一点,连接AC、BC,∠CAB=40°,∠ACB=90°,∠BAC的角平分线交MN于点D,点E是射线AD上的一个动点,连接CE、BE,∠CED的角平分线交MN于点F.当∠BEF=70°时,令,用含的式子表示∠EBC为( ).
A. B. C. D.
3.在中,,则为( )三角形.
A.锐角 B.直角 C.钝角 D.等腰
4.如图,AB和CD相交于点O,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1>∠4+∠5 D.∠2<∠5
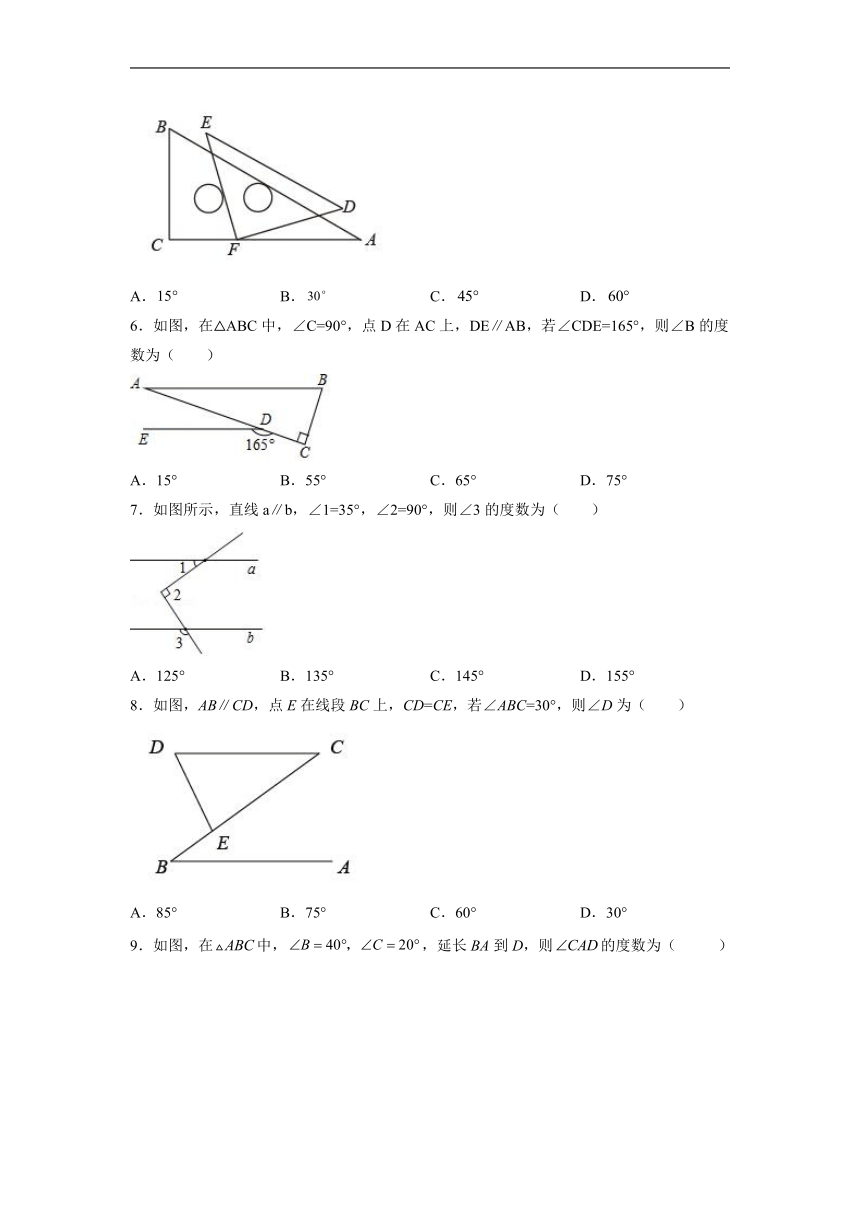
5.如图,将一副三角尺按图中所示位置摆放,点在上,其中,,,,,则的度数是( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=165°,则∠B的度数为( )
A.15° B.55° C.65° D.75°
7.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
8.如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D为( )
A.85° B.75° C.60° D.30°
9.如图,在中,,延长BA到D,则的度数为( )
A. B. C. D.
10.在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A=∠B=a∠C;④∠A∶∠B∶∠C=1∶2∶3,能确定△ABC为直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
11.如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=60°,则∠2的度数是( )
A.30° B.35° C.45° D.50°
12.如图,是的外角,若,,则( )
A. B. C. D.
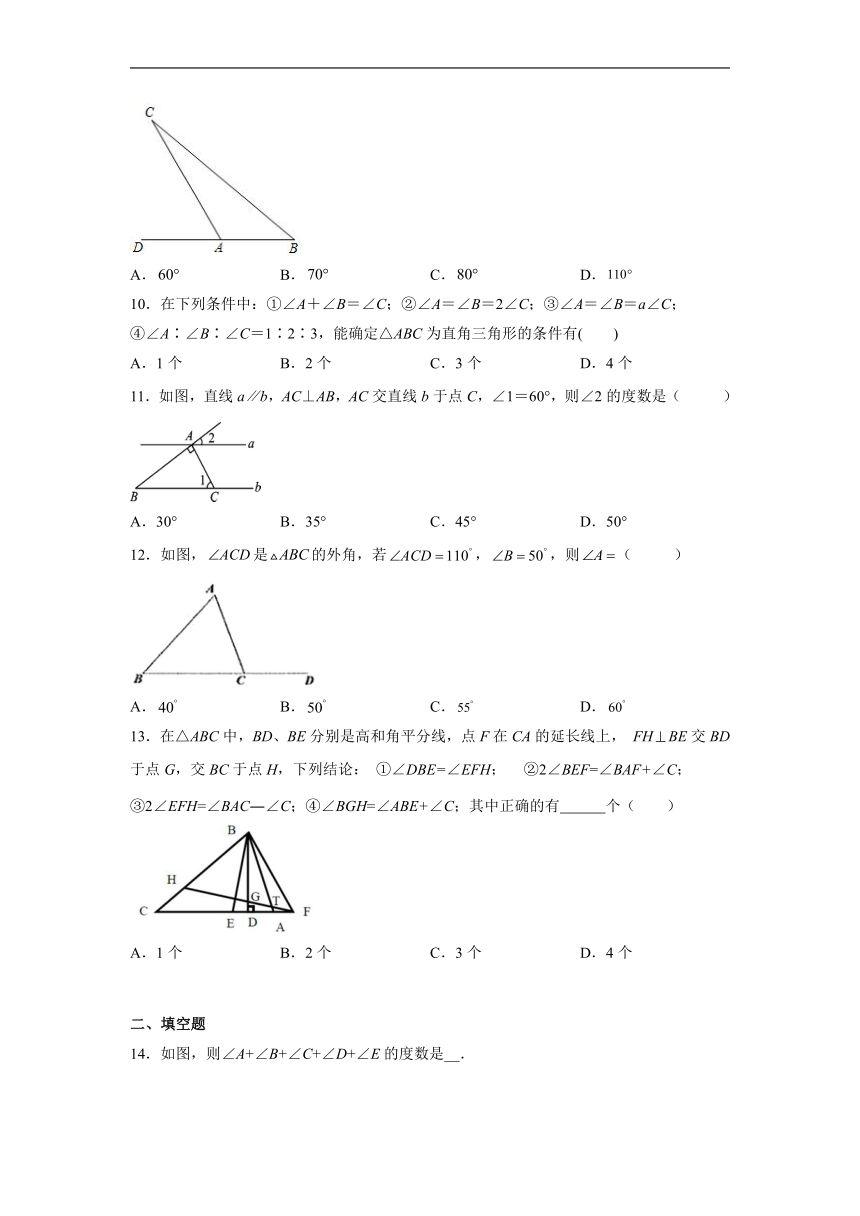
13.在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上, FHBE交BD于点G,交BC于点H,下列结论: ①∠DBE=∠EFH; ②2∠BEF=∠BAF+∠C;③2∠EFH=∠BAC―∠C;④∠BGH=∠ABE+∠C;其中正确的有 个( )
A.1个 B.2个 C.3个 D.4个
二、填空题
14.如图,则∠A+∠B+∠C+∠D+∠E的度数是__.
15.如图,,点为上一点,、的角平分线交于点,已知,则________度.
16.如图,在中,点是边上的一点,,,将沿折叠得到,与交于点,则 ______度.
17.在△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是________.
三、解答题
18.如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E.
(1)若AD⊥BC于D,∠C=40°,求∠DAE的度数;
(2)若EF⊥AE交AC于F,求证:∠C=2∠FEC.
19.如图,一个三角形的纸片ABC,其中∠A=∠C,
(1)把△ABC纸片按 (如图1) 所示折叠,使点A落在BC边上的点F处,DE是折痕.说明 BC∥DF;
(2)把△ABC纸片沿DE折叠,当点A落在四边形BCED内时 (如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;
(3)当点A落在四边形BCED外时 (如图3),探索∠C与∠1、∠2之间的大小关系.(直接写出结论)
20.如图,, .
(1)试说明;
(2)若,且,求的度数.
21.如图,在中,,,是的高,平分交于,求的度数.
参考答案
1--10CDBAA DABAB 11--13ADD
14.180°
15.
16.
17.140°
18.(1)证明:∵∠C=40°,∠B=2∠C,
∴∠B=80°,
∴∠BAC=60°,
∵AE平分∠BAC,
∴∠EAC=30°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=50°,
∴∠DAE=50°﹣30°=20°;
(2)证明:∵EF⊥AE,
∴∠AEF=90°,
∴∠AED+∠FEC=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∵AE平分∠BAC,
∴∠EAC=∠BAC=(180°﹣∠B﹣∠C)=(180°﹣3∠C)=90°﹣∠C,
∵∠DAE=∠DAC﹣∠EAC,
∴∠DAE=∠DAC﹣(90°﹣∠C)=90°﹣∠C﹣90°+∠C=∠C,
∴∠FEC=∠C,
∴∠C=2∠FEC.
19.解:(1) 由折叠知∠A=∠DFE,
∵∠A=∠C,
∴∠DFE=∠C,
∴BC∥DF;
(2)∠1+∠2=2∠A.理由如下:
∵∠1+2∠AED=180°, ∠2+2∠ADE=180°,
∴∠1+∠2+2(∠ADE+∠AED)=360°.
∵∠A+∠ADE+∠AED=180°,
∴∠ADE+∠AED=180°-∠A,
∴∠1+∠2+2(180°-A)=360°,
即∠1+∠2=2∠C.
(3)∠1-∠2=2∠A.
∵2∠AED+∠1=180°,2∠ADE-∠2=180°,
∴2(∠ADE+∠AED)+∠1-∠2=360°.
∵∠A+∠ADE+∠AED=180°,
∴∠ADE+∠AED=180°-∠A,
∴∠1-∠2+2(180°-∠A)=360°,
即∠1-∠2=2∠C.
20.(1)解:∵,∴BM∥CN,∴∠CBM=∠BCN,∵,∴∠3+∠CBM=∠4+∠BCN,即∠ABC=∠BCD,∴AB∥CD;
(2)解:∵∠ABD=∠EBF,,∴∠ABD=110°,∴∠BAD+∠BDA=70°,∵,∴∠BAD=35°,∵AB∥CD,∴∠ADC=∠BAD=35°.
21.解:∵,,
∴,
又平分,是的高,
∴,∠BAD=90°-∠B=90°-30°=60°,
∴∠DAE=60°-40°=20°.
一、单选题
1.如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )
A.90° B.95° C.100° D.150°
2.如图,直线,点C为直线MN上一点,连接AC、BC,∠CAB=40°,∠ACB=90°,∠BAC的角平分线交MN于点D,点E是射线AD上的一个动点,连接CE、BE,∠CED的角平分线交MN于点F.当∠BEF=70°时,令,用含的式子表示∠EBC为( ).
A. B. C. D.
3.在中,,则为( )三角形.
A.锐角 B.直角 C.钝角 D.等腰
4.如图,AB和CD相交于点O,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1>∠4+∠5 D.∠2<∠5
5.如图,将一副三角尺按图中所示位置摆放,点在上,其中,,,,,则的度数是( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=165°,则∠B的度数为( )
A.15° B.55° C.65° D.75°
7.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
8.如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D为( )
A.85° B.75° C.60° D.30°
9.如图,在中,,延长BA到D,则的度数为( )
A. B. C. D.
10.在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A=∠B=a∠C;④∠A∶∠B∶∠C=1∶2∶3,能确定△ABC为直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
11.如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=60°,则∠2的度数是( )
A.30° B.35° C.45° D.50°
12.如图,是的外角,若,,则( )
A. B. C. D.
13.在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上, FHBE交BD于点G,交BC于点H,下列结论: ①∠DBE=∠EFH; ②2∠BEF=∠BAF+∠C;③2∠EFH=∠BAC―∠C;④∠BGH=∠ABE+∠C;其中正确的有 个( )
A.1个 B.2个 C.3个 D.4个
二、填空题
14.如图,则∠A+∠B+∠C+∠D+∠E的度数是__.
15.如图,,点为上一点,、的角平分线交于点,已知,则________度.
16.如图,在中,点是边上的一点,,,将沿折叠得到,与交于点,则 ______度.
17.在△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是________.
三、解答题
18.如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E.
(1)若AD⊥BC于D,∠C=40°,求∠DAE的度数;
(2)若EF⊥AE交AC于F,求证:∠C=2∠FEC.
19.如图,一个三角形的纸片ABC,其中∠A=∠C,
(1)把△ABC纸片按 (如图1) 所示折叠,使点A落在BC边上的点F处,DE是折痕.说明 BC∥DF;
(2)把△ABC纸片沿DE折叠,当点A落在四边形BCED内时 (如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;
(3)当点A落在四边形BCED外时 (如图3),探索∠C与∠1、∠2之间的大小关系.(直接写出结论)
20.如图,, .
(1)试说明;
(2)若,且,求的度数.
21.如图,在中,,,是的高,平分交于,求的度数.
参考答案
1--10CDBAA DABAB 11--13ADD
14.180°
15.
16.
17.140°
18.(1)证明:∵∠C=40°,∠B=2∠C,
∴∠B=80°,
∴∠BAC=60°,
∵AE平分∠BAC,
∴∠EAC=30°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=50°,
∴∠DAE=50°﹣30°=20°;
(2)证明:∵EF⊥AE,
∴∠AEF=90°,
∴∠AED+∠FEC=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∵AE平分∠BAC,
∴∠EAC=∠BAC=(180°﹣∠B﹣∠C)=(180°﹣3∠C)=90°﹣∠C,
∵∠DAE=∠DAC﹣∠EAC,
∴∠DAE=∠DAC﹣(90°﹣∠C)=90°﹣∠C﹣90°+∠C=∠C,
∴∠FEC=∠C,
∴∠C=2∠FEC.
19.解:(1) 由折叠知∠A=∠DFE,
∵∠A=∠C,
∴∠DFE=∠C,
∴BC∥DF;
(2)∠1+∠2=2∠A.理由如下:
∵∠1+2∠AED=180°, ∠2+2∠ADE=180°,
∴∠1+∠2+2(∠ADE+∠AED)=360°.
∵∠A+∠ADE+∠AED=180°,
∴∠ADE+∠AED=180°-∠A,
∴∠1+∠2+2(180°-A)=360°,
即∠1+∠2=2∠C.
(3)∠1-∠2=2∠A.
∵2∠AED+∠1=180°,2∠ADE-∠2=180°,
∴2(∠ADE+∠AED)+∠1-∠2=360°.
∵∠A+∠ADE+∠AED=180°,
∴∠ADE+∠AED=180°-∠A,
∴∠1-∠2+2(180°-∠A)=360°,
即∠1-∠2=2∠C.
20.(1)解:∵,∴BM∥CN,∴∠CBM=∠BCN,∵,∴∠3+∠CBM=∠4+∠BCN,即∠ABC=∠BCD,∴AB∥CD;
(2)解:∵∠ABD=∠EBF,,∴∠ABD=110°,∴∠BAD+∠BDA=70°,∵,∴∠BAD=35°,∵AB∥CD,∴∠ADC=∠BAD=35°.
21.解:∵,,
∴,
又平分,是的高,
∴,∠BAD=90°-∠B=90°-30°=60°,
∴∠DAE=60°-40°=20°.
