人教版七年级上册 1.4.2 有理数的除法 (第1课时) 课件(共16张PPT)
文档属性
| 名称 | 人教版七年级上册 1.4.2 有理数的除法 (第1课时) 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 369.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
1.4.2 有理数的除法
(第1课时)
1.一个不等于0的有理数可看作由哪两个部分组成?
(符号、绝对值)
2.两个不等于0的有理数相乘,积的符号、积的绝对值是如何确定的?
同号得正,异号得负,因数绝对值的积作为积的绝对值.
3.计算: (1) 9×(-2) = (2) (- 9) × 2 =
(3) (-9) ×(-2) = (4) 0 ×a =
知识回顾
18
-18
-18
0
9
-2
-9
2
-9
-2
0
观察上面的结果,两个有理数相除,商的符号有什么规律 商的绝对值呢
(1)由9×(-2)=-18,得
(-18)÷(-2)=( ), (-18) ÷9 =( )
(2)由(- 9) × 2 =-18,得
(-18) ÷ (- 9 )=( ) ,(-18)÷2=( )
(3)由(- 9) ×(-2) = 18,得
18÷(-2)=( ), 18÷ (- 9 )=( )
(4)由0 ×a=0 , 得 0 ÷ a=( )
做一做
有理数除法法则
两个有理数相除,同号得 ,异号
得 ,并把绝对值 。
0除以任何非0的数都得 。
正
负
相除
零
例1 计算:
(1)(+12)÷(+4) (2) (-57)÷(+3)
(3) (-36)÷(-9) (4) (+96)÷(-16)
例2:化简下列各式:
-3
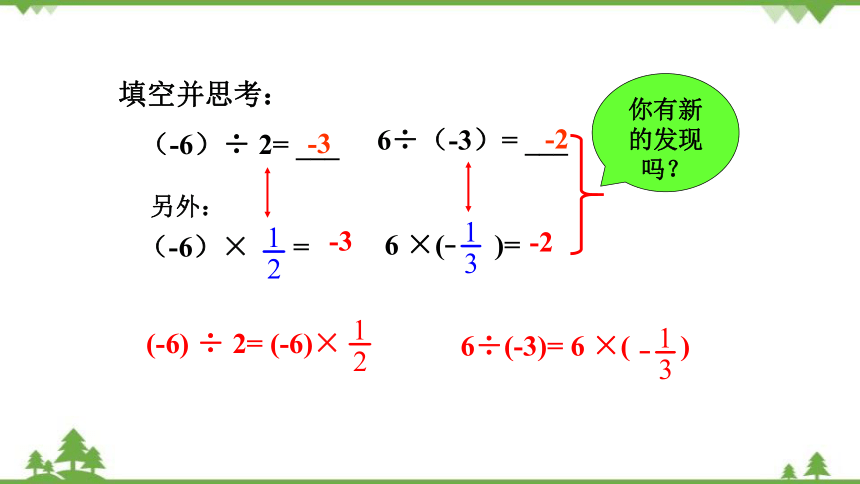
填空并思考:
-2
6÷(-3)= ___
(-6)÷ 2= ___
你有新的发现吗?
(-6)× =
6 ×( )=
另外:
-3
-2
(-6) ÷ 2= (-6)×
6÷(-3)= 6 ×( )
●
●
●
●
●
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
用式子表示成:
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数
有理数的减法与除法法则对比
有理数的减法法则
减去一个数,等于加这个数的相反数.
a - b = a + (-b)
减数变为相反数
减号变加号
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数
例3 计算:
(1) (-72) ÷9
解: (1) (-72) ÷9
(2)
= (-72) ×
= - 8
= - 8
(1) (-72) ÷9
= - (72÷9)
两个有理数相除,有两种方法:
(1)两数直接相除:两数相除,同号得正,异号得负,并把绝对值相除;
(2)把除法转化为乘法: 除以一个不等于0的数, 等于乘以这个数的倒数.
如(-78) ÷3= ______, 运用第______种方法较简便.
= ______,用上述______种方法较简便.
一
二
在进行有理数除法运算时,在能整除的情况下,往往采用两数直接相除.在不能整除的情况下,则往往采用把除法转化为乘法.
-26
-10
1、判断:
(1)若两数相除结果为正,则这两个数同正或同负。( )
(2) 零除任何数,都等于零。 ( )
(3)零没有倒数。 ( )
(4)任何数的倒数都不会大于它本身。 ( )
(5) ( )
(6) ( )
√
×
√
×
√
×
随堂练习
2 、填空:
(1)(-8) ÷ ____ = - 4 (2) _____÷( )= 3
(3) =____ (4)(-0.48)÷(-8)= ___
3、a、b为有理数,若 = 0,则( )
A. b=0 B. b=0且a≠0
C. a=0且b=0 D. a=0且b≠0
4、下列运算错误的是( )
A. ÷ (-2) =2×(-2) B. 8 ÷ (- 4) = -2
C. (-4) ÷ = (-4) ×(-2) C. 0 ÷ (-3) =0
随堂练习
2
-1
7
0.06
B
A
5 、计算:
(1)
(2)
随堂练习
二、有理数的除法法则(二)
两数相除,同号得正,异号得负,并把绝对值相除,0除以任何一个不等于0的数,都得0.
三、注意: 1. 0不能做除数
2. 一般在不能整除的情况下用第一法则,
在能整除的情况下应用第二法则.
一、有理数除法法则(一)
除以一个不等于0的数,等于乘这个数的倒数.
即 a÷b=a· (b≠0).
课堂小结
1、习题1.4 第4题
1.4.2 有理数的除法
(第1课时)
1.一个不等于0的有理数可看作由哪两个部分组成?
(符号、绝对值)
2.两个不等于0的有理数相乘,积的符号、积的绝对值是如何确定的?
同号得正,异号得负,因数绝对值的积作为积的绝对值.
3.计算: (1) 9×(-2) = (2) (- 9) × 2 =
(3) (-9) ×(-2) = (4) 0 ×a =
知识回顾
18
-18
-18
0
9
-2
-9
2
-9
-2
0
观察上面的结果,两个有理数相除,商的符号有什么规律 商的绝对值呢
(1)由9×(-2)=-18,得
(-18)÷(-2)=( ), (-18) ÷9 =( )
(2)由(- 9) × 2 =-18,得
(-18) ÷ (- 9 )=( ) ,(-18)÷2=( )
(3)由(- 9) ×(-2) = 18,得
18÷(-2)=( ), 18÷ (- 9 )=( )
(4)由0 ×a=0 , 得 0 ÷ a=( )
做一做
有理数除法法则
两个有理数相除,同号得 ,异号
得 ,并把绝对值 。
0除以任何非0的数都得 。
正
负
相除
零
例1 计算:
(1)(+12)÷(+4) (2) (-57)÷(+3)
(3) (-36)÷(-9) (4) (+96)÷(-16)
例2:化简下列各式:
-3
填空并思考:
-2
6÷(-3)= ___
(-6)÷ 2= ___
你有新的发现吗?
(-6)× =
6 ×( )=
另外:
-3
-2
(-6) ÷ 2= (-6)×
6÷(-3)= 6 ×( )
●
●
●
●
●
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
用式子表示成:
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数
有理数的减法与除法法则对比
有理数的减法法则
减去一个数,等于加这个数的相反数.
a - b = a + (-b)
减数变为相反数
减号变加号
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数
例3 计算:
(1) (-72) ÷9
解: (1) (-72) ÷9
(2)
= (-72) ×
= - 8
= - 8
(1) (-72) ÷9
= - (72÷9)
两个有理数相除,有两种方法:
(1)两数直接相除:两数相除,同号得正,异号得负,并把绝对值相除;
(2)把除法转化为乘法: 除以一个不等于0的数, 等于乘以这个数的倒数.
如(-78) ÷3= ______, 运用第______种方法较简便.
= ______,用上述______种方法较简便.
一
二
在进行有理数除法运算时,在能整除的情况下,往往采用两数直接相除.在不能整除的情况下,则往往采用把除法转化为乘法.
-26
-10
1、判断:
(1)若两数相除结果为正,则这两个数同正或同负。( )
(2) 零除任何数,都等于零。 ( )
(3)零没有倒数。 ( )
(4)任何数的倒数都不会大于它本身。 ( )
(5) ( )
(6) ( )
√
×
√
×
√
×
随堂练习
2 、填空:
(1)(-8) ÷ ____ = - 4 (2) _____÷( )= 3
(3) =____ (4)(-0.48)÷(-8)= ___
3、a、b为有理数,若 = 0,则( )
A. b=0 B. b=0且a≠0
C. a=0且b=0 D. a=0且b≠0
4、下列运算错误的是( )
A. ÷ (-2) =2×(-2) B. 8 ÷ (- 4) = -2
C. (-4) ÷ = (-4) ×(-2) C. 0 ÷ (-3) =0
随堂练习
2
-1
7
0.06
B
A
5 、计算:
(1)
(2)
随堂练习
二、有理数的除法法则(二)
两数相除,同号得正,异号得负,并把绝对值相除,0除以任何一个不等于0的数,都得0.
三、注意: 1. 0不能做除数
2. 一般在不能整除的情况下用第一法则,
在能整除的情况下应用第二法则.
一、有理数除法法则(一)
除以一个不等于0的数,等于乘这个数的倒数.
即 a÷b=a· (b≠0).
课堂小结
1、习题1.4 第4题
