鲁教版(五四制)数学七年级下册 7.4 二元一次方程与一次函数(1) 教案
文档属性
| 名称 | 鲁教版(五四制)数学七年级下册 7.4 二元一次方程与一次函数(1) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 18:43:07 | ||
图片预览


文档简介
基于翻转课堂模式的教学设计
----记《二元一次方程与一次函数第一课时》
一、背景介绍
实验版的课标对本节课的要求是“能根据一次函数的图象求二元一次方程组的近似解”,新课标改为“体会一次函数与二元一次方程的关系”,由注重知识技能目标的实现改为注重过程性目标的实现,让学生能参与到数学活动中,在具体的情景中初步认识方程与函数,方程组与函数的关系,并从中获得一些经验。新课标更注重学生的学习过程、学习体验,更体现生本课堂.
本节课学生的接受和理解是比较难的.根据以往的教学经验,出现这样几种情况;一是老师讲的头头是道,自认为非常清晰明了,但学生一脸茫然;二是看似探究过、讨论过、总结过,但落实比较差;三是课上完了,学生不知道学习这些有什么用,导致遗忘特别快 .新的版本对本节安排了两课时,第一节探究二元一次方程与一次函数,二元一次方程组与一次函数的关系,第二节探究两点法确定一次函数表达式和在实际生活中的应用.在认真研读课标和教材的基础上对本节课做如下设计:
二、教学过程设计
前一天学生自学,完成自主学习任务单。课前小组内讨论解决自主学习任务单中的问题,教师走进学生,倾听学生的想法.
课前自主学习任务单
一、学习指南
1.课题名称:7.7 二元一次方程与一次函数第一课时
2.达成目标: (1)查阅资料,能完成相应的学习任务 (2)初步感知二元一次方程与一次函数的关系,初步感知二元一次方程组与一次函数的关系
3.学习方法建议:查阅资料,自主探究,交流展示
二、学习任务
学习任务 学习过程 学习建议
任务一: 复习回顾 1、解方程组 2、画出一次函数的图象. 知识回顾 自主完成
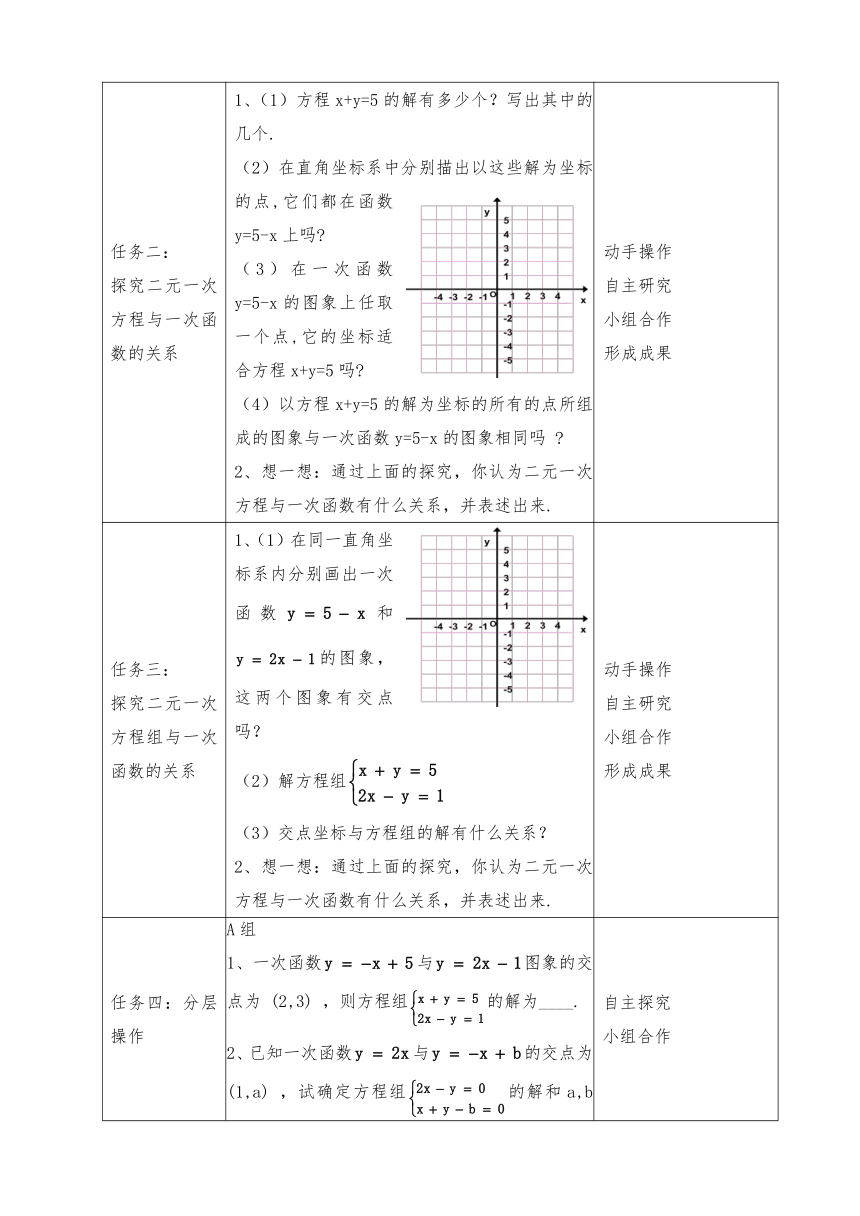
任务二: 探究二元一次方程与一次函数的关系 1、(1)方程x+y=5的解有多少个?写出其中的几个. (2)在直角坐标系中分别描出以这些解为坐标的点,它们都在函数y=5-x上吗 (3)在一次函数y=5-x的图象上任取一个点,它的坐标适合方程x+y=5吗 (4)以方程x+y=5的解为坐标的所有的点所组成的图象与一次函数y=5-x的图象相同吗 2、想一想:通过上面的探究,你认为二元一次方程与一次函数有什么关系,并表述出来. 动手操作 自主研究 小组合作 形成成果
任务三: 探究二元一次方程组与一次函数的关系 1、(1)在同一直角坐标系内分别画出一次函数和的图象,这两个图象有交点吗? (2)解方程组 (3)交点坐标与方程组的解有什么关系? 2、想一想:通过上面的探究,你认为二元一次方程与一次函数有什么关系,并表述出来. 动手操作 自主研究 小组合作 形成成果
任务四:分层操作 A组 1、一次函数与图象的交点为 (2,3) ,则方程组的解为____. 2、已知一次函数与的交点为(1,a) ,试确定方程组的解和a,b的值. B组 已知二元一次方程组无解,求a的值. 自主探究 小组合作
任务五: 展示交流研究成果 我们展示的方式:__________________ 将你们小组的自学成果呈现给大家(PPT、视频、图片、文稿等).
任务六: 学后反思 总结学习成果: 1、我收获的知识:__________________ 2、我提升的能力: _________________ 3、我要努力的方面:________________ 评价自我学习成果和其他小组的学习成果. 2.评价方式: 优秀:三颗星 良好:两颗星 一般:一颗星
活动一:明确问题
师:前面我们学习了一元一次方程与一次函数,本章我们又学习了二元一次方程,在此基础上,今天,我们来研究二元一次方程与一次函数.
(教师板书课题)
师:你能把二元一次方程改写成______的形式吗?
生:.
师:是不是任意的二元一次方程都能进行这样的改写呢?
生:是.
师:通过移项任意的二元一次方程都可以改写为的形式,那么两者之间还有哪些关系呢?昨天借助自主学习任务单我们已对这部分进行了自学,而且课下以及课前小组内也讨论交流了,下面我们就请小组代表跟我们一起分享他们的自学成果吧!
活动二:成果汇报
(一)探究二元一次方程与一次函数的关系
根据学生自己的学习经验,请小组代表来说说他们的理解.多请几个小组展示他们的想法,给学生充分的时间和机会来表达自己的对这一问题的认识,以便了解学情.
根据学生的理解,教师及时做出补充和总结.
师:对于方程的每一组解对应图象上的一个点,图象上的每个点的坐标都满足对应的二元一次方程这一关系,这里老师给出一种解释.
(几何画板动态展示验证这两种对应,尤其是图象上的每一个点的坐标都满足对应的方程)(对于其它情况一并做出解释)
师:好,通过以上研究我们知道每一个二元一次方程都对应一个一次函数,一次函数的图象是由无数个点组成的,每个点的坐标都满足对应的二元一次方程,同时,二元一次方程的解有无数组,每一组都对应图象上的一个点,也就是方程的解和图象上的点是一一对应的(边总结边板书).实际上,一次函数、一次函数图像和二元一次方程所表达的关系是一样的,只是表达形式不同而已.
(二)探究二元一次方程组与一次函数的关系
师:那么你能把对应的一次函数写出来吗?
生:.
师:现在我用大括号一连,变成了二元一次方程组,那么方程组与对应的两个一次函数之间又有什么关系呢?这是我们自主学习任务单上的任务三,哪个小组来展示?
同样让学生说说他们认为两者之间有什么关系.根据实际情况教师及时做出反馈和总结.(一般地,从图形的角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线交点的坐标.)
师:好,通过上面的研究,一个二元一次方程组对应两个一次函数,并且方程组的解和函数图象的交点坐标是相对应的(教师板书).下面考考你的眼力如何.
活动三:基础夯实
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),则方程组的解为_______;
2、一次函数y=5-x与y=2x-1图象的交点为(2,3),则对应方程组____________的解.
3、(1)根据下列图象,你能说出对应方程组的解吗
(2)你能说出上图是哪些方程组的解
4、根据下列图象,你能说出对应方程组的解吗
师:通过上面的练习,你有何体会?
生:当两条直线只有一个交点时,对应的方程组有一个解;当两条直线平行时,对应的方程组没有解;当两条直线重合时,对应的方程组有无数解.(估计到这里学生能较轻松的得出结论)
师:非常好,也就是直线的位置关系与方程组解的情况是相对应的.
活动四:应用提高
师:那么反过来,给你方程组你能直观的把解表示在图上吗?尝试完成解二元一次方程组.
生板演,完成后给大家讲一讲做题的步骤:写出对应的一次函数 作出图像 读出交点坐标 写出方程组的解.(若总结不出教师帮忙)
师:这样我们得到一种新的解二元一次方程组的方法——图象法.根据你的做题经验,你能说说图象法的优点和不足吗?
生:我觉得图象法比较直观,但由于作图有误差结果会不精确.
师:同意吗?虽然有一定的误差,但是图象法可以用来估算方程组的解.这种解决问题的思路和方法在实际生活中也有广泛的应用,请大家完成本题:一家电信公司给顾客提供上网费的两种计费方式:方式A以每分0.1元的价格按上网时间计费;方式B除收月基费20元外再以每分0.05元的价格按上网时间计费.
(1)上网时间为多少分时,两种方式的计费相等?
(2)当上网时间290分钟时,选择哪种计费方式比较合算?
两位同学板书过程.教师巡视学生的做题情况.学生完成之后先小组内交流做法.然后请两位学生讲讲他们的思路.
方法一; 方法二;
解: 解:
(1) (1)同方法一
(2)作出函数图象
(2)当x=400时,
所以选方式A比较合算.
由图得,当x=290时方式A花费较少,所以选A.(若选则作图的话估计绝大多数学生的图象会如上图)
生;老师,我觉得图象需要改一下,这里,所以只保留第一象限的部分.(希望有学生能发现,若发现不了结合实际问题教师提醒)
师:非常仔细,这样更完美.方法一是计算,是从“数”的角度,方法二是作图,是从“形”的方面,再次印证了对于“数”的问题可以转化为“形”,“形”的问题可以从“数”的角度来考虑.
活动五:总结升华
师:以上就本节课主要内容,①你有哪些收获?对同学和自己有哪些提示?还有哪些困惑?②今天学习的内容是怎样研究的?蕴含着哪些数学思想?
同桌先说一说.学生七嘴八舌,说说自己的收获,然后师生共同总结.
三、设计反思
翻转课堂翻转了传统的教学结构,学生学习知识在课外,内化知识在课内.在课外自主学习,提出问题,整理收获;在课内学生交流展示,协作学习,解疑答惑,教师巡视,进行个性化指导.翻转课堂是以学生为核心,教师为学生学习的设计者、指导者、帮助者,这种模式能有效提升学生的自主学习能力,发展学生思维能力.
翻转课堂落实的一个关键是制作好自主学习任务单,本课在设计时以任务驱动和问题导向为原则,六个任务环环相扣,层层深入.任务一复习方程组的解法和一次函数图象的画法,为下面任务的展开打下基础.任务二和任务三的通过问题串引导学生观察思考,给学生提供一个很好的抓手,并要求学生将探究的结果用自己喜欢的方式表述出来,这也是本节课的难点之一,这样提高学生思考的深度和广度,锻炼表达能力.通过任务四检测自学情况.通过任务五和任务六总结自己的学习.课前学生小组内先说说自己的看法,有哪些疑惑能解决,有哪些不能解决;交流展示环节大家畅所欲言,充分展示了研究问题的过程,找到方程与函数,方程组与函数的关系,教师及时归纳总结“数”与“形”是可以相互转化;知识应用环节通过看图读数直观感受数形结合思想,通过作图体会图象法可以估算方程组的解,然后再回到实际生活中,体会数形结合的直观性,体会数学来源于生活又服务于生活.在总结升华环节,一是对课堂内容作总结,使本节课知识形成一个整体,并纳入已有的知识体系;二是对研究的思路方法进行总结,让学生明确研究方程与函数的关系是从方程的解和函数图象入手的,为继续研究方程与函数、方程与不等式的关系打好基础,培养学生的创新意识和变式能力.
----记《二元一次方程与一次函数第一课时》
一、背景介绍
实验版的课标对本节课的要求是“能根据一次函数的图象求二元一次方程组的近似解”,新课标改为“体会一次函数与二元一次方程的关系”,由注重知识技能目标的实现改为注重过程性目标的实现,让学生能参与到数学活动中,在具体的情景中初步认识方程与函数,方程组与函数的关系,并从中获得一些经验。新课标更注重学生的学习过程、学习体验,更体现生本课堂.
本节课学生的接受和理解是比较难的.根据以往的教学经验,出现这样几种情况;一是老师讲的头头是道,自认为非常清晰明了,但学生一脸茫然;二是看似探究过、讨论过、总结过,但落实比较差;三是课上完了,学生不知道学习这些有什么用,导致遗忘特别快 .新的版本对本节安排了两课时,第一节探究二元一次方程与一次函数,二元一次方程组与一次函数的关系,第二节探究两点法确定一次函数表达式和在实际生活中的应用.在认真研读课标和教材的基础上对本节课做如下设计:
二、教学过程设计
前一天学生自学,完成自主学习任务单。课前小组内讨论解决自主学习任务单中的问题,教师走进学生,倾听学生的想法.
课前自主学习任务单
一、学习指南
1.课题名称:7.7 二元一次方程与一次函数第一课时
2.达成目标: (1)查阅资料,能完成相应的学习任务 (2)初步感知二元一次方程与一次函数的关系,初步感知二元一次方程组与一次函数的关系
3.学习方法建议:查阅资料,自主探究,交流展示
二、学习任务
学习任务 学习过程 学习建议
任务一: 复习回顾 1、解方程组 2、画出一次函数的图象. 知识回顾 自主完成
任务二: 探究二元一次方程与一次函数的关系 1、(1)方程x+y=5的解有多少个?写出其中的几个. (2)在直角坐标系中分别描出以这些解为坐标的点,它们都在函数y=5-x上吗 (3)在一次函数y=5-x的图象上任取一个点,它的坐标适合方程x+y=5吗 (4)以方程x+y=5的解为坐标的所有的点所组成的图象与一次函数y=5-x的图象相同吗 2、想一想:通过上面的探究,你认为二元一次方程与一次函数有什么关系,并表述出来. 动手操作 自主研究 小组合作 形成成果
任务三: 探究二元一次方程组与一次函数的关系 1、(1)在同一直角坐标系内分别画出一次函数和的图象,这两个图象有交点吗? (2)解方程组 (3)交点坐标与方程组的解有什么关系? 2、想一想:通过上面的探究,你认为二元一次方程与一次函数有什么关系,并表述出来. 动手操作 自主研究 小组合作 形成成果
任务四:分层操作 A组 1、一次函数与图象的交点为 (2,3) ,则方程组的解为____. 2、已知一次函数与的交点为(1,a) ,试确定方程组的解和a,b的值. B组 已知二元一次方程组无解,求a的值. 自主探究 小组合作
任务五: 展示交流研究成果 我们展示的方式:__________________ 将你们小组的自学成果呈现给大家(PPT、视频、图片、文稿等).
任务六: 学后反思 总结学习成果: 1、我收获的知识:__________________ 2、我提升的能力: _________________ 3、我要努力的方面:________________ 评价自我学习成果和其他小组的学习成果. 2.评价方式: 优秀:三颗星 良好:两颗星 一般:一颗星
活动一:明确问题
师:前面我们学习了一元一次方程与一次函数,本章我们又学习了二元一次方程,在此基础上,今天,我们来研究二元一次方程与一次函数.
(教师板书课题)
师:你能把二元一次方程改写成______的形式吗?
生:.
师:是不是任意的二元一次方程都能进行这样的改写呢?
生:是.
师:通过移项任意的二元一次方程都可以改写为的形式,那么两者之间还有哪些关系呢?昨天借助自主学习任务单我们已对这部分进行了自学,而且课下以及课前小组内也讨论交流了,下面我们就请小组代表跟我们一起分享他们的自学成果吧!
活动二:成果汇报
(一)探究二元一次方程与一次函数的关系
根据学生自己的学习经验,请小组代表来说说他们的理解.多请几个小组展示他们的想法,给学生充分的时间和机会来表达自己的对这一问题的认识,以便了解学情.
根据学生的理解,教师及时做出补充和总结.
师:对于方程的每一组解对应图象上的一个点,图象上的每个点的坐标都满足对应的二元一次方程这一关系,这里老师给出一种解释.
(几何画板动态展示验证这两种对应,尤其是图象上的每一个点的坐标都满足对应的方程)(对于其它情况一并做出解释)
师:好,通过以上研究我们知道每一个二元一次方程都对应一个一次函数,一次函数的图象是由无数个点组成的,每个点的坐标都满足对应的二元一次方程,同时,二元一次方程的解有无数组,每一组都对应图象上的一个点,也就是方程的解和图象上的点是一一对应的(边总结边板书).实际上,一次函数、一次函数图像和二元一次方程所表达的关系是一样的,只是表达形式不同而已.
(二)探究二元一次方程组与一次函数的关系
师:那么你能把对应的一次函数写出来吗?
生:.
师:现在我用大括号一连,变成了二元一次方程组,那么方程组与对应的两个一次函数之间又有什么关系呢?这是我们自主学习任务单上的任务三,哪个小组来展示?
同样让学生说说他们认为两者之间有什么关系.根据实际情况教师及时做出反馈和总结.(一般地,从图形的角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线交点的坐标.)
师:好,通过上面的研究,一个二元一次方程组对应两个一次函数,并且方程组的解和函数图象的交点坐标是相对应的(教师板书).下面考考你的眼力如何.
活动三:基础夯实
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),则方程组的解为_______;
2、一次函数y=5-x与y=2x-1图象的交点为(2,3),则对应方程组____________的解.
3、(1)根据下列图象,你能说出对应方程组的解吗
(2)你能说出上图是哪些方程组的解
4、根据下列图象,你能说出对应方程组的解吗
师:通过上面的练习,你有何体会?
生:当两条直线只有一个交点时,对应的方程组有一个解;当两条直线平行时,对应的方程组没有解;当两条直线重合时,对应的方程组有无数解.(估计到这里学生能较轻松的得出结论)
师:非常好,也就是直线的位置关系与方程组解的情况是相对应的.
活动四:应用提高
师:那么反过来,给你方程组你能直观的把解表示在图上吗?尝试完成解二元一次方程组.
生板演,完成后给大家讲一讲做题的步骤:写出对应的一次函数 作出图像 读出交点坐标 写出方程组的解.(若总结不出教师帮忙)
师:这样我们得到一种新的解二元一次方程组的方法——图象法.根据你的做题经验,你能说说图象法的优点和不足吗?
生:我觉得图象法比较直观,但由于作图有误差结果会不精确.
师:同意吗?虽然有一定的误差,但是图象法可以用来估算方程组的解.这种解决问题的思路和方法在实际生活中也有广泛的应用,请大家完成本题:一家电信公司给顾客提供上网费的两种计费方式:方式A以每分0.1元的价格按上网时间计费;方式B除收月基费20元外再以每分0.05元的价格按上网时间计费.
(1)上网时间为多少分时,两种方式的计费相等?
(2)当上网时间290分钟时,选择哪种计费方式比较合算?
两位同学板书过程.教师巡视学生的做题情况.学生完成之后先小组内交流做法.然后请两位学生讲讲他们的思路.
方法一; 方法二;
解: 解:
(1) (1)同方法一
(2)作出函数图象
(2)当x=400时,
所以选方式A比较合算.
由图得,当x=290时方式A花费较少,所以选A.(若选则作图的话估计绝大多数学生的图象会如上图)
生;老师,我觉得图象需要改一下,这里,所以只保留第一象限的部分.(希望有学生能发现,若发现不了结合实际问题教师提醒)
师:非常仔细,这样更完美.方法一是计算,是从“数”的角度,方法二是作图,是从“形”的方面,再次印证了对于“数”的问题可以转化为“形”,“形”的问题可以从“数”的角度来考虑.
活动五:总结升华
师:以上就本节课主要内容,①你有哪些收获?对同学和自己有哪些提示?还有哪些困惑?②今天学习的内容是怎样研究的?蕴含着哪些数学思想?
同桌先说一说.学生七嘴八舌,说说自己的收获,然后师生共同总结.
三、设计反思
翻转课堂翻转了传统的教学结构,学生学习知识在课外,内化知识在课内.在课外自主学习,提出问题,整理收获;在课内学生交流展示,协作学习,解疑答惑,教师巡视,进行个性化指导.翻转课堂是以学生为核心,教师为学生学习的设计者、指导者、帮助者,这种模式能有效提升学生的自主学习能力,发展学生思维能力.
翻转课堂落实的一个关键是制作好自主学习任务单,本课在设计时以任务驱动和问题导向为原则,六个任务环环相扣,层层深入.任务一复习方程组的解法和一次函数图象的画法,为下面任务的展开打下基础.任务二和任务三的通过问题串引导学生观察思考,给学生提供一个很好的抓手,并要求学生将探究的结果用自己喜欢的方式表述出来,这也是本节课的难点之一,这样提高学生思考的深度和广度,锻炼表达能力.通过任务四检测自学情况.通过任务五和任务六总结自己的学习.课前学生小组内先说说自己的看法,有哪些疑惑能解决,有哪些不能解决;交流展示环节大家畅所欲言,充分展示了研究问题的过程,找到方程与函数,方程组与函数的关系,教师及时归纳总结“数”与“形”是可以相互转化;知识应用环节通过看图读数直观感受数形结合思想,通过作图体会图象法可以估算方程组的解,然后再回到实际生活中,体会数形结合的直观性,体会数学来源于生活又服务于生活.在总结升华环节,一是对课堂内容作总结,使本节课知识形成一个整体,并纳入已有的知识体系;二是对研究的思路方法进行总结,让学生明确研究方程与函数的关系是从方程的解和函数图象入手的,为继续研究方程与函数、方程与不等式的关系打好基础,培养学生的创新意识和变式能力.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
