2022-2023学年高一上学期数学人教B版(2019)必修第一册第二章 等式与不等式 章末小结练习(Word含解析)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教B版(2019)必修第一册第二章 等式与不等式 章末小结练习(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 63.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-03 12:51:08 | ||
图片预览


文档简介
第二章章末小结
一、单项选择题
1.已知集合A={x|x2-5x-14<0},B={x|5x-10<0},则A∪B=( ).
A.{x|-2-2}
2.若m<0,n>0,且m+n<0,则下列不等式中成立的是( ).
A.-n3.不等式<0的解集为( ).
A.{x|x>1}
B.{x|x<-2}
C.{x|-2D.{x|x>1或x<-2}
4.已知a>1,b>1,记M=+,N=,则M与N的大小关系为( ).
A.M>N B.M=N C.M5.已知当x>0时,不等式x2+ax+1≥0恒成立,则a的最小值是( ).
A.0 B.-2 C.-3 D.-
6.若不等式ax2+bx+c>0的解集为{x|-2A.{x|x<-或x>}
B.{x|-3C.{x|-1D.{x|x<-3或x>1}
7.某辆汽车以x km/h的速度在高速公路上匀速行驶(考虑到高速公路行车安全,要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为(x-k+)L,其中k为常数.若汽车以120 km/h的速度行驶时,每小时的油耗为11.5 L,则欲使每小时的油耗不超过9 L,速度x的取值范围为( ).
A.40≤x≤60 B.50≤x≤80 C.40≤x≤80 D.60≤x≤100
8.若两个正实数x,y满足=1,且不等式x+A.{m|-1B.{m|m<-1或m>4}
C.{m|-4D.{m|m<0或m>3}
二、多项选择题
9.下列说法中,正确的是( ).
A.若a>b>0,则ac2>bc2
B.若aab>b2
C.若a>b>0且c<0,则>
D.若a>b且,则ab>0
10.已知p:x≥m,q:2+x-x2<0,下列给出的实数m的值,能使p是q的充分不必要条件的是( ).
A.m=2 B.m= C.m=3 D.m=-1
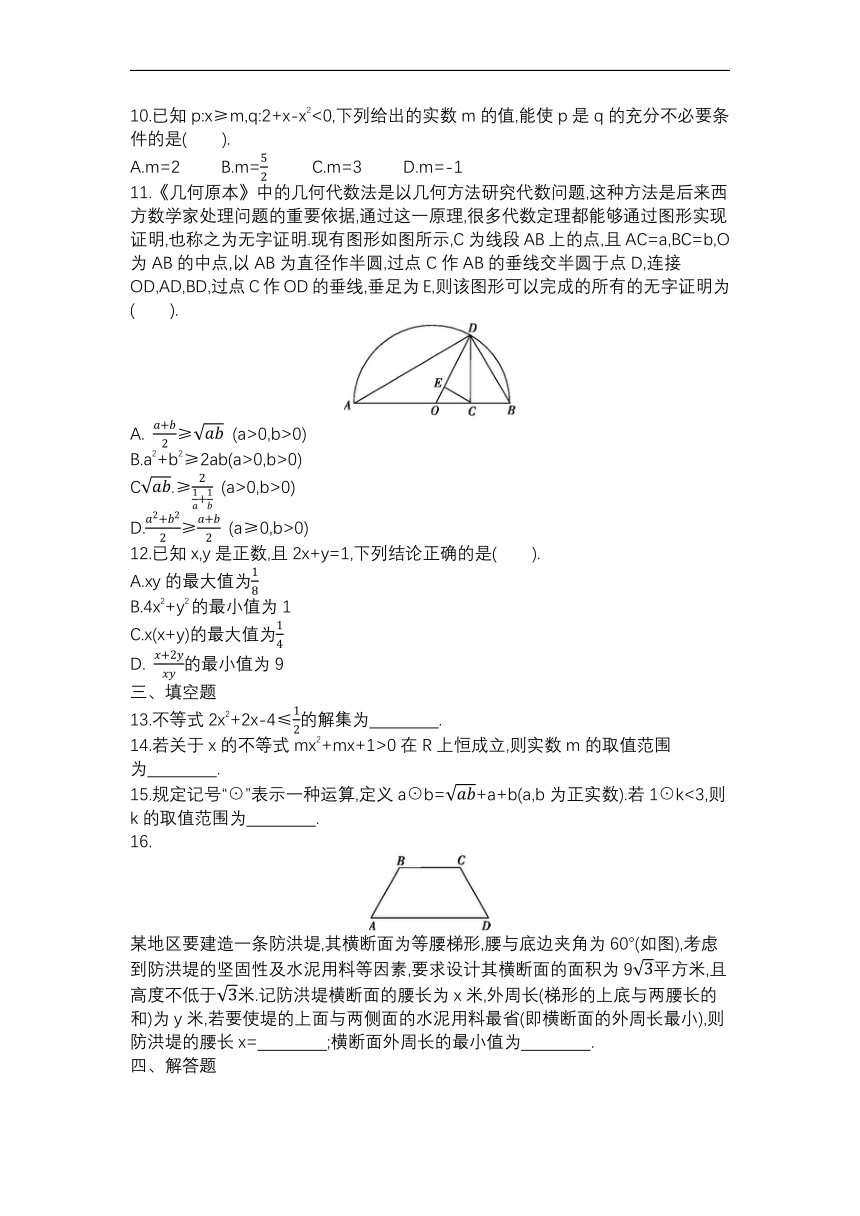
11.《几何原本》中的几何代数法是以几何方法研究代数问题,这种方法是后来西方数学家处理问题的重要依据,通过这一原理,很多代数定理都能够通过图形实现证明,也称之为无字证明.现有图形如图所示,C为线段AB上的点,且AC=a,BC=b,O为AB的中点,以AB为直径作半圆,过点C作AB的垂线交半圆于点D,连接OD,AD,BD,过点C作OD的垂线,垂足为E,则该图形可以完成的所有的无字证明为( ).
A. ≥ (a>0,b>0)
B.a2+b2≥2ab(a>0,b>0)
C.≥ (a>0,b>0)
D.≥ (a≥0,b>0)
12.已知x,y是正数,且2x+y=1,下列结论正确的是( ).
A.xy的最大值为
B.4x2+y2的最小值为1
C.x(x+y)的最大值为
D. 的最小值为9
三、填空题
13.不等式2x2+2x-4≤的解集为 .
14.若关于x的不等式mx2+mx+1>0在R上恒成立,则实数m的取值范围为 .
15.规定记号“☉”表示一种运算,定义a☉b=+a+b(a,b为正实数).若1☉k<3,则k的取值范围为 .
16.
某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边夹角为60°(如图),考虑到防洪堤的坚固性及水泥用料等因素,要求设计其横断面的面积为9平方米,且高度不低于米.记防洪堤横断面的腰长为x米,外周长(梯形的上底与两腰长的和)为y米,若要使堤的上面与两侧面的水泥用料最省(即横断面的外周长最小),则防洪堤的腰长x= ;横断面外周长的最小值为 .
四、解答题
17.在①x+(x>1)的最小值是a,②不等式(1-a)x2-4x+6>0的解集是{x|-3已知 .
(1)解不等式2x2+(2-a)x-a>0.
(2)当b为何值时,ax2+bx+3≥0的解集为R
18.求y=(x>3)的取值范围.
19.(1)解不等式:>1.
(2)若不等式x2-2x-1>a的解集为R,求实数a的取值范围.
20.已知y=x2-a+x+1.
(1)当a=时,解不等式y≤0;
(2)若a>0,解关于x的不等式y≤0.
21.已知y=x2+ax+3.
(1)若a=-,试求 (x>0)的最小值;
(2)当-1≤x≤1时,y>a恒成立,求a的取值范围.
22.随着“新冠”疫情得到有效控制,企业进入了复工复产阶段.为了支持一家小微企业发展,某科创公司研发了一种玩具供其生产销售.根据测算,该企业每月生产该种玩具的成本p由两部分费用(单位:元)构成:①固定成本(与生产玩具套数x无关),总计2万元;②生产所需成本为5x+x2.
(1)该企业每月生产多少套玩具时,可使得平均每套所需的成本费用最少 此时每套玩具的成本费用是多少
(2)因疫情防控的需要,要求企业的复工复产逐步进行,假设复工后,企业每月生产x套,售价(单位:元)定为30+且每月生产出的玩具能全部售出.若企业的月产量与复工率成正比,且该企业复工率达100%时的月产量为4000套,则该企业的复工率至少达到多少时,才能确保月利润不少于10万元
参考答案
1.C 【解析】解不等式x2-5x-14<0得-2解不等式5x-10<0得x<2,所以B={x|x<2}.
所以A∪B={x|x<7}.
2.D 【解析】(法一:取特殊值法)令m=-3,n=2,分别代入各选项检验,可知D正确.
(法二)m+n<0 m<-n,n<-m,由于m<03.C 【解析】原不等式等价于(x-1)(x+2)<0,则原不等式的解集为{x|-24.A 【解析】M=+=≥>,故选A.
5.B 【解析】原不等式可化为a≥-x-,因为-x-≤-2,当且仅当x=1时等号成立,所以a≥-2,则a的最小值为-2.
6.D 【解析】由已知得方程ax2+bx+c=0的两个根分别为x1=-2,x2=1且a<0,∴=1,=-2,∴不等式ax2+(a+b)x+c-a<0可化为x2+1+x+-1>0,
即x2+2x-3>0,解得x<-3或x>1.
7.D 【解析】因为汽车以120 km/h的速度行驶时,每小时的油耗为11.5 L,所以120-k+=11.5,解得k=100,故每小时的油耗为x+-20L.依题意,x+-20≤9,解得45≤x≤100.又因为60≤x≤120,所以60≤x≤100.
8.B 【解析】因为不等式x+因为x>0,y>0,且+=1,所以x+=x++=++2≥2+2=4,
当且仅当=,即x=2,y=8时取“=”,所以x+min=4,故m2-3m>4,
即(m+1)(m-4)>0,解得m<-1或m>4,
所以实数m的取值范围是{m|m>4或m<-1}.
9.BC 【解析】当c=0时,ac2=bc2,故A错误; a2>ab, ab>b2,∴a2>ab>b2,故B正确;由a>b>0,可得a2>b2,∴<,又c<0,∴根据不等式的性质,可得>,故C正确;若a>b,则b-a<0,由-=>0,可得ab<0,故D错误.
10.BC 【解析】记A={x|x≥m},对于q:2+x-x2<0,记B={x|x<-1或x>2}.由p是q的充分不必要条件,得A是B的真子集,所以m>2,故B,C成立.
11.AC 【解析】∵AC=a,BC=b,∠ADB=,
∴根据图形,在Rt△ADB中,由射影定理得CD2=AC·CB,∴CD2=ab,即CD=.
∵OD≥CD,且OD==,∴≥(a>0,b>0),当且仅当a=b时取等号,即A正确;
在Rt△OCD中,同理得CD2=DE·OD,∴DE===,
又∵CD≥DE,∴≥=(a>0,b>0),当且仅当a=b时取等号,即C正确.故选AC.
12.AD 【解析】因为x>0,y>0,所以1=2x+y≥2,所以xy≤,当且仅当x=,y=时等号成立,所以xy的最大值为,故A正确;
因为4x2+y2=4x2+(1-2x)2=8x2-4x+1=8x-2+,又y=1-2x>0,即0x(x+y)=x(x+1-2x)=-x2+x=-x-2+,因为0=+=(2x+y)+=5++≥5+2=9,当且仅当x=y=时等号成立,故D正确.
13. 【解析】由4x2+4x-8≤1,得4x2+4x-9≤0,解得-≤x≤.
14.0≤m<4 【解析】因为关于x的不等式mx2+mx+1>0在R上恒成立,所以分以下两种情况讨论:
①当m=0时,可得1>0,符合题意;
②当m≠0时,有解得0综上所述,实数m的取值范围是0≤m<4.
15.016.2 6 【解析】设横断面的高为h,
由题意得AD=BC+2·=BC+x,h=x,
∴9=(AD+BC)h=(2BC+x)·x,
故BC=-,
由得2≤x<6,
∴y=BC+2x=+ (2≤x<6),
从而y=+≥2 =6,当且仅当=(2≤x<6),即x=2时等号成立.
17.【解析】若选①,因为x>1,所以x+=(x-1)++1≥2+1=3,
当且仅当x-1=,即x=2时等号成立.
故最小值为3.所以a=3.
(1)不等式2x2+(2-a)x-a>0,即2x2-x-3>0,解得x<-1或x>,
所以所求不等式的解集为xx<-1或x>.
(2)ax2+bx+3≥0,即3x2+bx+3≥0,若此不等式的解集为R,则Δ=b2-4×3×3≤0,所以-6≤b≤6.
若选②,由题意知1-a<0且-3和1是方程(1-a)x2-4x+6=0的两根,所以解得a=3.
(1)不等式2x2+(2-a)x-a>0,即2x2-x-3>0,解得x<-1或x>,
所以所求不等式的解集为xx<-1或x>.
(2)ax2+bx+3≥0,即3x2+bx+3≥0,若此不等式的解集为R,则Δ=b2-4×3×3≤0,所以-6≤b≤6.
18.【解析】∵x>3,∴x-3>0,
∴y===2(x-3)++12≥2+12=24,
当且仅当2(x-3)=,即x=6时,上式等号成立,
∴y=(x>3)的取值范围是y≥24.
19.【解析】(1)原不等式移项并化简,得>0,即<0,等价于(2x-3)(x-2)<0,
解得所以该不等式的解集为x(2)因为不等式x2-2x-1>a的解集为R,
所以x2-2x-1-a>0在R上恒成立,
则函数y=x2-2x-1-a的图像恒在x轴上方,与x轴无交点,
从而一元二次方程x2-2x-1-a=0无实数根,
所以Δ=22-4×(-1-a)<0,
解得a<-2.
故实数a的取值范围为a<-2.
20.【解析】(1)当a=时,有不等式y=x2-x+1≤0,
∴x-(x-2)≤0,
∴不等式y≤0的解集为.
(2)∵不等式y=x-(x-a)≤0,
∴当0a,
该不等式的解集为;
当a>1时,有当a=1时,该不等式的解集为{x|x=1}.
21.【解析】(1)当a=-时,=x+-≥2-=,
当且仅当x=,即x=时,等号成立.
∴(x>0)的最小值为.
(2)当-1≤x≤1时,不等式x2+ax+3>a x2+3>a(1-x).
∵-1≤x≤1,∴0≤1-x≤2.
当x=1时,1-x=0,x2+3>a(1-x)对一切a∈R恒成立;
当x≠1时,0<1-x≤2,则a<,
∵==(1-x)+-2≥2-2=2,
当且仅当1-x=,即x=-1时,取到等号,
∴min=2,从而a<2.
综上所述,a的取值范围为a<2.
22.【解析】(1)依题意,p=20000+5x+x2,则=+x+5≥2+5=25,
当且仅当=x,即x=2000时取等号,
所以每月生产2000套玩具时,可使平均每套所需的成本费用最少,此时每套玩具的成本费用为25元.
(2)设月利润为s元,则s=x30+-20000+5x+x2=+25x-20000≥100000,
所以x2+5000x-24000000≥0,即(x+8000)(x-3000)≥0,
所以x≥3000,所以=75%,
所以该企业的复工率至少达到75%时,才能确保月利润不少于10万元.
一、单项选择题
1.已知集合A={x|x2-5x-14<0},B={x|5x-10<0},则A∪B=( ).
A.{x|-2
2.若m<0,n>0,且m+n<0,则下列不等式中成立的是( ).
A.-n
A.{x|x>1}
B.{x|x<-2}
C.{x|-2
4.已知a>1,b>1,记M=+,N=,则M与N的大小关系为( ).
A.M>N B.M=N C.M
A.0 B.-2 C.-3 D.-
6.若不等式ax2+bx+c>0的解集为{x|-2
B.{x|-3
7.某辆汽车以x km/h的速度在高速公路上匀速行驶(考虑到高速公路行车安全,要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为(x-k+)L,其中k为常数.若汽车以120 km/h的速度行驶时,每小时的油耗为11.5 L,则欲使每小时的油耗不超过9 L,速度x的取值范围为( ).
A.40≤x≤60 B.50≤x≤80 C.40≤x≤80 D.60≤x≤100
8.若两个正实数x,y满足=1,且不等式x+
C.{m|-4
二、多项选择题
9.下列说法中,正确的是( ).
A.若a>b>0,则ac2>bc2
B.若a
C.若a>b>0且c<0,则>
D.若a>b且,则ab>0
10.已知p:x≥m,q:2+x-x2<0,下列给出的实数m的值,能使p是q的充分不必要条件的是( ).
A.m=2 B.m= C.m=3 D.m=-1
11.《几何原本》中的几何代数法是以几何方法研究代数问题,这种方法是后来西方数学家处理问题的重要依据,通过这一原理,很多代数定理都能够通过图形实现证明,也称之为无字证明.现有图形如图所示,C为线段AB上的点,且AC=a,BC=b,O为AB的中点,以AB为直径作半圆,过点C作AB的垂线交半圆于点D,连接OD,AD,BD,过点C作OD的垂线,垂足为E,则该图形可以完成的所有的无字证明为( ).
A. ≥ (a>0,b>0)
B.a2+b2≥2ab(a>0,b>0)
C.≥ (a>0,b>0)
D.≥ (a≥0,b>0)
12.已知x,y是正数,且2x+y=1,下列结论正确的是( ).
A.xy的最大值为
B.4x2+y2的最小值为1
C.x(x+y)的最大值为
D. 的最小值为9
三、填空题
13.不等式2x2+2x-4≤的解集为 .
14.若关于x的不等式mx2+mx+1>0在R上恒成立,则实数m的取值范围为 .
15.规定记号“☉”表示一种运算,定义a☉b=+a+b(a,b为正实数).若1☉k<3,则k的取值范围为 .
16.
某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边夹角为60°(如图),考虑到防洪堤的坚固性及水泥用料等因素,要求设计其横断面的面积为9平方米,且高度不低于米.记防洪堤横断面的腰长为x米,外周长(梯形的上底与两腰长的和)为y米,若要使堤的上面与两侧面的水泥用料最省(即横断面的外周长最小),则防洪堤的腰长x= ;横断面外周长的最小值为 .
四、解答题
17.在①x+(x>1)的最小值是a,②不等式(1-a)x2-4x+6>0的解集是{x|-3
(1)解不等式2x2+(2-a)x-a>0.
(2)当b为何值时,ax2+bx+3≥0的解集为R
18.求y=(x>3)的取值范围.
19.(1)解不等式:>1.
(2)若不等式x2-2x-1>a的解集为R,求实数a的取值范围.
20.已知y=x2-a+x+1.
(1)当a=时,解不等式y≤0;
(2)若a>0,解关于x的不等式y≤0.
21.已知y=x2+ax+3.
(1)若a=-,试求 (x>0)的最小值;
(2)当-1≤x≤1时,y>a恒成立,求a的取值范围.
22.随着“新冠”疫情得到有效控制,企业进入了复工复产阶段.为了支持一家小微企业发展,某科创公司研发了一种玩具供其生产销售.根据测算,该企业每月生产该种玩具的成本p由两部分费用(单位:元)构成:①固定成本(与生产玩具套数x无关),总计2万元;②生产所需成本为5x+x2.
(1)该企业每月生产多少套玩具时,可使得平均每套所需的成本费用最少 此时每套玩具的成本费用是多少
(2)因疫情防控的需要,要求企业的复工复产逐步进行,假设复工后,企业每月生产x套,售价(单位:元)定为30+且每月生产出的玩具能全部售出.若企业的月产量与复工率成正比,且该企业复工率达100%时的月产量为4000套,则该企业的复工率至少达到多少时,才能确保月利润不少于10万元
参考答案
1.C 【解析】解不等式x2-5x-14<0得-2
所以A∪B={x|x<7}.
2.D 【解析】(法一:取特殊值法)令m=-3,n=2,分别代入各选项检验,可知D正确.
(法二)m+n<0 m<-n,n<-m,由于m<0
5.B 【解析】原不等式可化为a≥-x-,因为-x-≤-2,当且仅当x=1时等号成立,所以a≥-2,则a的最小值为-2.
6.D 【解析】由已知得方程ax2+bx+c=0的两个根分别为x1=-2,x2=1且a<0,∴=1,=-2,∴不等式ax2+(a+b)x+c-a<0可化为x2+1+x+-1>0,
即x2+2x-3>0,解得x<-3或x>1.
7.D 【解析】因为汽车以120 km/h的速度行驶时,每小时的油耗为11.5 L,所以120-k+=11.5,解得k=100,故每小时的油耗为x+-20L.依题意,x+-20≤9,解得45≤x≤100.又因为60≤x≤120,所以60≤x≤100.
8.B 【解析】因为不等式x+
当且仅当=,即x=2,y=8时取“=”,所以x+min=4,故m2-3m>4,
即(m+1)(m-4)>0,解得m<-1或m>4,
所以实数m的取值范围是{m|m>4或m<-1}.
9.BC 【解析】当c=0时,ac2=bc2,故A错误; a2>ab, ab>b2,∴a2>ab>b2,故B正确;由a>b>0,可得a2>b2,∴<,又c<0,∴根据不等式的性质,可得>,故C正确;若a>b,则b-a<0,由-=>0,可得ab<0,故D错误.
10.BC 【解析】记A={x|x≥m},对于q:2+x-x2<0,记B={x|x<-1或x>2}.由p是q的充分不必要条件,得A是B的真子集,所以m>2,故B,C成立.
11.AC 【解析】∵AC=a,BC=b,∠ADB=,
∴根据图形,在Rt△ADB中,由射影定理得CD2=AC·CB,∴CD2=ab,即CD=.
∵OD≥CD,且OD==,∴≥(a>0,b>0),当且仅当a=b时取等号,即A正确;
在Rt△OCD中,同理得CD2=DE·OD,∴DE===,
又∵CD≥DE,∴≥=(a>0,b>0),当且仅当a=b时取等号,即C正确.故选AC.
12.AD 【解析】因为x>0,y>0,所以1=2x+y≥2,所以xy≤,当且仅当x=,y=时等号成立,所以xy的最大值为,故A正确;
因为4x2+y2=4x2+(1-2x)2=8x2-4x+1=8x-2+,又y=1-2x>0,即0
13. 【解析】由4x2+4x-8≤1,得4x2+4x-9≤0,解得-≤x≤.
14.0≤m<4 【解析】因为关于x的不等式mx2+mx+1>0在R上恒成立,所以分以下两种情况讨论:
①当m=0时,可得1>0,符合题意;
②当m≠0时,有解得0
15.0
由题意得AD=BC+2·=BC+x,h=x,
∴9=(AD+BC)h=(2BC+x)·x,
故BC=-,
由得2≤x<6,
∴y=BC+2x=+ (2≤x<6),
从而y=+≥2 =6,当且仅当=(2≤x<6),即x=2时等号成立.
17.【解析】若选①,因为x>1,所以x+=(x-1)++1≥2+1=3,
当且仅当x-1=,即x=2时等号成立.
故最小值为3.所以a=3.
(1)不等式2x2+(2-a)x-a>0,即2x2-x-3>0,解得x<-1或x>,
所以所求不等式的解集为xx<-1或x>.
(2)ax2+bx+3≥0,即3x2+bx+3≥0,若此不等式的解集为R,则Δ=b2-4×3×3≤0,所以-6≤b≤6.
若选②,由题意知1-a<0且-3和1是方程(1-a)x2-4x+6=0的两根,所以解得a=3.
(1)不等式2x2+(2-a)x-a>0,即2x2-x-3>0,解得x<-1或x>,
所以所求不等式的解集为xx<-1或x>.
(2)ax2+bx+3≥0,即3x2+bx+3≥0,若此不等式的解集为R,则Δ=b2-4×3×3≤0,所以-6≤b≤6.
18.【解析】∵x>3,∴x-3>0,
∴y===2(x-3)++12≥2+12=24,
当且仅当2(x-3)=,即x=6时,上式等号成立,
∴y=(x>3)的取值范围是y≥24.
19.【解析】(1)原不等式移项并化简,得>0,即<0,等价于(2x-3)(x-2)<0,
解得
所以x2-2x-1-a>0在R上恒成立,
则函数y=x2-2x-1-a的图像恒在x轴上方,与x轴无交点,
从而一元二次方程x2-2x-1-a=0无实数根,
所以Δ=22-4×(-1-a)<0,
解得a<-2.
故实数a的取值范围为a<-2.
20.【解析】(1)当a=时,有不等式y=x2-x+1≤0,
∴x-(x-2)≤0,
∴不等式y≤0的解集为.
(2)∵不等式y=x-(x-a)≤0,
∴当0
该不等式的解集为;
当a>1时,有
21.【解析】(1)当a=-时,=x+-≥2-=,
当且仅当x=,即x=时,等号成立.
∴(x>0)的最小值为.
(2)当-1≤x≤1时,不等式x2+ax+3>a x2+3>a(1-x).
∵-1≤x≤1,∴0≤1-x≤2.
当x=1时,1-x=0,x2+3>a(1-x)对一切a∈R恒成立;
当x≠1时,0<1-x≤2,则a<,
∵==(1-x)+-2≥2-2=2,
当且仅当1-x=,即x=-1时,取到等号,
∴min=2,从而a<2.
综上所述,a的取值范围为a<2.
22.【解析】(1)依题意,p=20000+5x+x2,则=+x+5≥2+5=25,
当且仅当=x,即x=2000时取等号,
所以每月生产2000套玩具时,可使平均每套所需的成本费用最少,此时每套玩具的成本费用为25元.
(2)设月利润为s元,则s=x30+-20000+5x+x2=+25x-20000≥100000,
所以x2+5000x-24000000≥0,即(x+8000)(x-3000)≥0,
所以x≥3000,所以=75%,
所以该企业的复工率至少达到75%时,才能确保月利润不少于10万元.
