人教版七年级上册1.1正数和负数课件(共24张PPT)
文档属性
| 名称 | 人教版七年级上册1.1正数和负数课件(共24张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 285.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
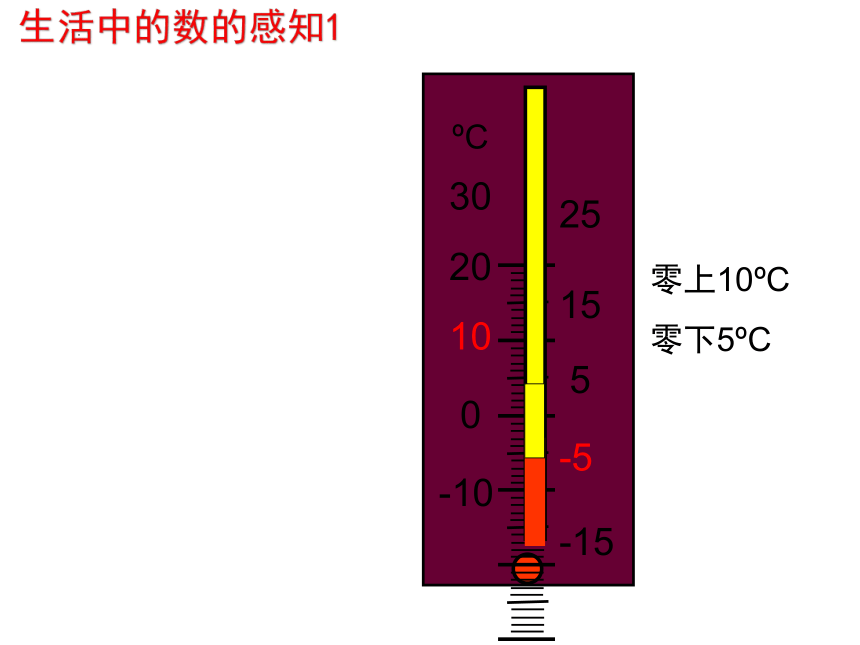
生活中的数的感知1
30
20
10
0
-10
25
15
5
-5
-15
C
零上10 C
零下5 C
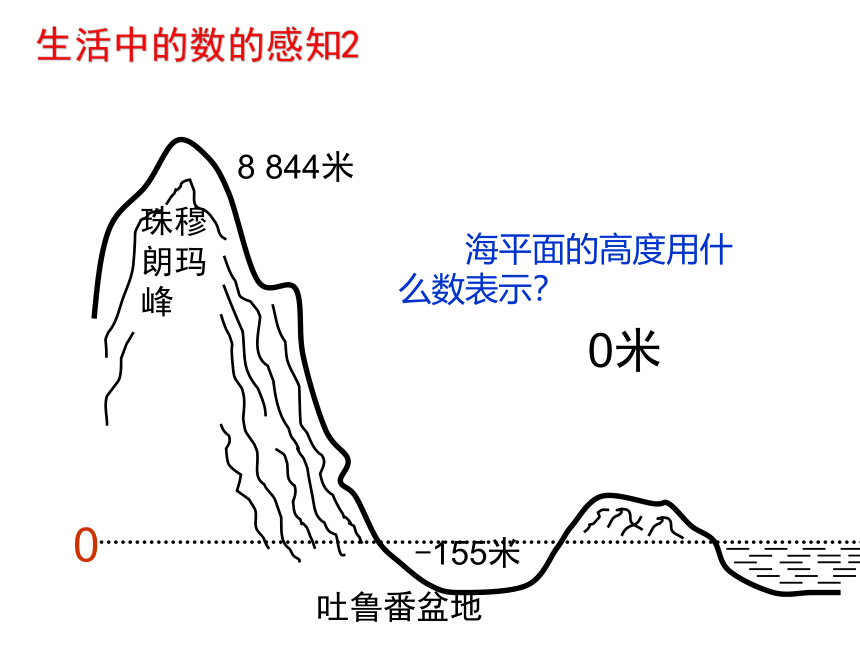
珠穆朗玛峰
8 844米
吐鲁番盆地
-155米
海平面的高度用什 么数表示?
0米
0
生活中的数的感知2
1.1 正数与负数
七年级数学(上册) 人教版
第一章 有理数
七年级数学组
主 备 人:
议课组长:
议课日期:2022.8.29
授课日期:2022.9
学习目标(1分钟)
1、了解负数是从实际需要中产生的.
2、掌握正数和负数概念和表示方法;会判断一个数是正数还是负数;
3、理解正数、负数及0的意义,
4、中考考点:用正负数表示具有相反意义的量。
自学课本P2 的内容, 思考:
1、什么是正数?什么是负数? 0是最小的数吗?
2、“0” 这个数有什么特点?+0是正数吗?-0呢?
3、书写正数和负数应注意什么?
自学指导1(4分钟)
像1, +3,1.8%这样 的数叫做 .
正数
大于0
像-3,-1.6,-2.7%这样在 前面加上符号 , (负)的数叫做 .( 0的数)
正数
“-”
负数
小于
不是负数
不是正数
正数与负数的
0既 ,也 ,是中性数,是 分界
一般地,一个数由 组成。
两部分(符号和数字)
如:+5=5.如:-5≠5
正数前面的“+”通常省略;
负数前面的“-”不可省略
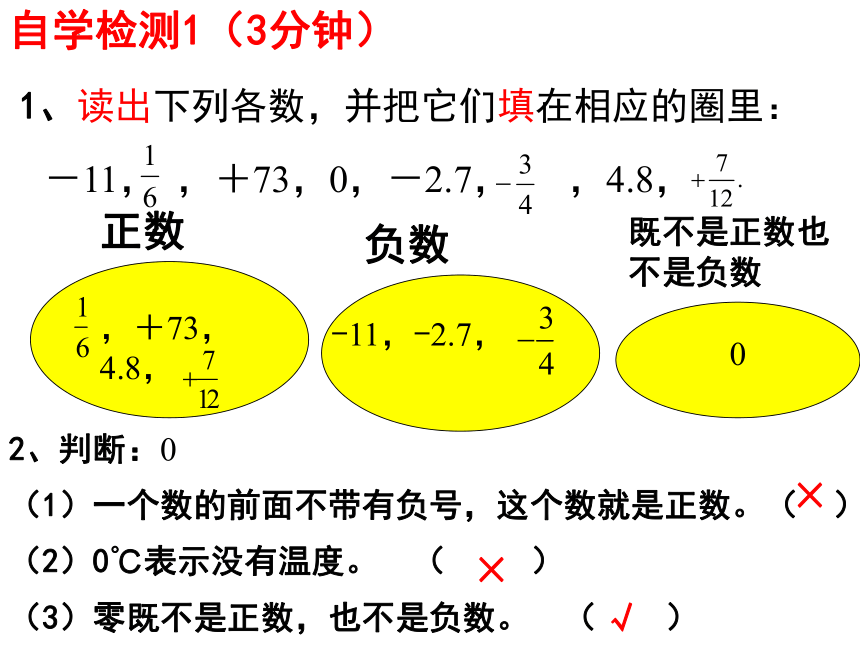
-11, ,+73,0,-2.7, ,4.8,
1、读出下列各数,并把它们填在相应的圈里:
正数
负数
,+73,4.8,
-11,-2.7,
-11,-2.7,-
自学检测1(3分钟)
2、判断:0
(1)一个数的前面不带有负号,这个数就是正数。( )
(2)0℃表示没有温度。 ( )
(3)零既不是正数,也不是负数。 ( )
√
×
×
既不是正数也
不是负数
0
自学检测1(3分钟)
3、小丽说:“一个数,如果不是正数,必定就是负数。”你认为她说的对吗?为什么?
解:不对,0既不是正数也不是负数。
不是正数的数是0或负数
不是负数的数是0或正数
非负数
非正数
4.下列语句正确的是 ( )
A.0℃表示没有温度
B.0表示什么也没有
C.0是非正数
D.0既可以看作是正数又可以看作是负数
C
变式训练.下列语句正确的有 ( )
①0常用来表示某些量的基准数
②0只表示什么也没有
③0是整数
④0是正数和负数的分界点
⑤0是非正数
A.1个 B.2个 C.3个 D.4个
D
笔记
1.如何区分一个数是正数还是负数
首先找0,然后看性质符号;
不含“+”“-”号,或者只含“+”号,
或者“-”号的个数是偶数则为正数。否则为负数。
知识点拨
0只表示没有吗
1.空罐中的金币数量0个;2.温度中的0℃;
3.海平面的高度0m;4.标准水位0m;
5.身高比较的基准0m; ……
0是正负数的分界点.它不再简简单单的只表示没有,它具有丰富的意义,如
0可以用来表示基准,一般地,高于基准的量用正数表示,低于基准的量用负数表示
2.
阅读课本P3例题,完成以下任务:
1、举出几对具有相反意义的量。
2、说说如何用正负数表示具有相反意义的量?
3、若选定150cm作为标准,你的身高表示为多少?
4、完成课本P3的练习。
自学指导2(5分钟)
零上 与零下
盈利 与亏损
加分 与扣分
高出 与低于
向东 与向西
具有相反意义
具有相反意义:上升与下降、增与减、收入与支出、胜与负、进与退、多与少、盈利与亏损、向东与向西、顺与逆、过剩与不足、重与轻等
如果有两个量是同类量,但表示的意义相反,那么这两个量就叫做具有相反意义的量
100C
40C
8元 5元
10分 15分
10米 5米
8米 4米
的量
1、具有相反意义的量。
什么是具有相反意义的量?
成对出现
用正数和负数可以表示同一个问题中具有相反意义的量
在具有相反意义的两个量中,任意规定其中一个量用正数表示,那么与这个量意义相反的量就用负数来表示。注意基准,一般基准是0.
例如:把上涨3.6%记为+3.6%,
那么下跌0.6%记作-0.6%
读作:正3.6%
读作:负0.6%
2、如何用正负数表示同一个问题中具有相反意义的量?
意义相反,有数量,同类量
一般规定:按指定方向变化的用正数表示
3、若选定150cm作为标准,你的身高表示为多少?
4、课本P3的练习答案
1、解:规定增加记为“+”,减少记为“-”,则:2010年为+108.7mm; 2009年为-81.5 mm; 2008年为+53.5 mm.
2.解:这个物体又移动了-1 m表示物体向左移动了1m这时物体又回到了原来的位置.
1、下列语句正确的是( )
A、“黑色”和“白色”是具有相反意义的量。
B、盈利200元和出口300箱是具有相反意义的量。
C、“向北4.5米”和“向南4.5米”是具有相反意 义的量。
D、“+15米”就表示向东走了15米。
自学检测2 (7分钟)
C
2、下列各量可用正、负数来表示的是( )
A、向北走3千米,向东走3千米。
B、甲班有男生25人,女生20人。
C、上午气温零上29℃,下午气温零上18℃.
D、上升200米,下降150米。
D
3、数学考试85分以上为优秀,老师将某一小组
的四名学生的数学分数以85分为标准,分别记
作:+10,-5,0,+15,则这四名同学的实际
成绩分别是______; _____; ______ ;______。
4、在某次乒乓球质量检测中,一只乒乓球超出
标准质量0.02克记作+0.02克,那么-0.03克
表示 ___________________。
95分
80分
85分
100分
轻于标准质量0.03克
5正负数表示的意义
(1)如果收入 120元记作+120元,那么-70元表示__________;
(2)如果蚂蚁向上爬 30 cm记作+30 cm,那么-10 cm表示_________________________;
(3)温度下降-5 ℃表示__________________;
(4)体重增加-3 kg表示__________________.
6、说出下列语句的实际意义
(1)小刚向西走了-100米;
(2)指针按顺时针旋转了-30°
解:小刚向东走了100米
解:指针按逆时针旋转了30 °
学生讨论、更正,教师点拨。
。
小结(2分钟)
你这节课学到了什么?
1、理解正数、负数的概念;会区分一个数是正数还是负数;
2、用正负数表示同一个问题中相反意义的量 (中考考点3分);
3、负数和0的意义。
注意:有的要带单位
1、如果水位升高3m时水位变化记作+3m,那么水位下降3m时水位变化记作( )
A. -3m B.3m C.6m D.-6m
A
2、(变式)如果收入80元记作+80元,那么支出记作( )
A. +20元 B. -20元 C. +100元 D. -100元
B
3.(1)东、西为两个相反方向,如果-4米表示一个物体向西运动4米,那么+2米表示____________,物体原地不动记作________;
(2)某仓库运进面粉7.5吨记为+7.5吨,那么运出3.8吨应记作_________。
向东运动2米
0米
-3.8吨
当堂训练:(15分钟)
(3)如果中午12时记作0时,下午3时记作+3时,上午9时记作 。
-3时
4、 如若把警戒水位定为0 m,水位高于警戒水位1.6m记
作_______ ,水位低于警戒水位0.2m时,记作 ;
+1.6m
-0.2m
5、(变式)南京长江大桥桥头堡的顶端高出地面约70米,
可记作 ,桥头堡的地基打入地下约30米深
的岩层,可记作
+70m
-30m
6、在有理数-3,0,23,-85,3.7中,属于非负数的个数有( )
A.4个 B.3个 C.2个 D.1个
B
7、某市某一天的最高温度是零上5℃,最低温度是零下5℃。如何表示这一天的最高气温和最低气温?
8、(变式)珠穆朗玛峰高于海平面8848米,吐鲁番盆地低于海平面155米,“高于”和“低于”其意义是相反的。如何表示它们的高度?
解:最高气温: 5℃;最低气温:- 5℃
解:珠穆朗玛峰高8848m;吐鲁番盆地-155m
正数:___________________________
负数:___________________________
既不是正数,也不是负数:________________
9、将下列各数按要求分别填入相应的横线上:
板书
1、正数、负数的概念;
2、区分一个数是正数还是负数
首先找0,然后看符号;不含“+”“-”号,或者只含“+”号,或者“-”号的个数是偶数则为正数。否则为负数。
2、用正负数表示同一个问题中相反意义的量 (中考考点3分);
3、0的意义。
注意:有的要带单位
10、(选做题)找规律:
(1)1,-2,3,-4,5,-6,7,-8 ,……其中第199个数为 _____ ,第2002个数_____ ,规律是_ _____________;
(2)1,2,-3,4,5,-6,7,8 ,-9 ……
其中第345个数为 _____ ,第2002个数_____ ,
规律是 _______ _______ ;
(3)-1,2,-3,4,-5,6,-7,8 ,-9……其中第279个数为 _____ ,第320个数的符号为___,规律是___ ___________;
199
-2002
奇数为+,偶数为-
-345
2002
3的倍数为-,其它为+
-279
+
奇数为-,偶数为+
数阵找规律和图形找规律
题型:
技巧:
标序列号和提公因式
找规律法就是从给出的特殊量中寻找其一般规律的方法,对于按照一定的顺序给出的一系列量,我们要根据已知的量找出其一般排列规律,通常可采用标序列号法找规律。
比较给出的数和序列号变化情况:1.符号变化情况、 2.数字变化情况,就很容易找出其变化规律.符号及数字与位置数之间的关系:
1.奇数位置上的数的符号为“一”,偶数位置上的数的符号为“+”(奇负偶正)
2.各个位置上的数(不考虑符号) 位置数的关系式 。
生活中的数的感知1
30
20
10
0
-10
25
15
5
-5
-15
C
零上10 C
零下5 C
珠穆朗玛峰
8 844米
吐鲁番盆地
-155米
海平面的高度用什 么数表示?
0米
0
生活中的数的感知2
1.1 正数与负数
七年级数学(上册) 人教版
第一章 有理数
七年级数学组
主 备 人:
议课组长:
议课日期:2022.8.29
授课日期:2022.9
学习目标(1分钟)
1、了解负数是从实际需要中产生的.
2、掌握正数和负数概念和表示方法;会判断一个数是正数还是负数;
3、理解正数、负数及0的意义,
4、中考考点:用正负数表示具有相反意义的量。
自学课本P2 的内容, 思考:
1、什么是正数?什么是负数? 0是最小的数吗?
2、“0” 这个数有什么特点?+0是正数吗?-0呢?
3、书写正数和负数应注意什么?
自学指导1(4分钟)
像1, +3,1.8%这样 的数叫做 .
正数
大于0
像-3,-1.6,-2.7%这样在 前面加上符号 , (负)的数叫做 .( 0的数)
正数
“-”
负数
小于
不是负数
不是正数
正数与负数的
0既 ,也 ,是中性数,是 分界
一般地,一个数由 组成。
两部分(符号和数字)
如:+5=5.如:-5≠5
正数前面的“+”通常省略;
负数前面的“-”不可省略
-11, ,+73,0,-2.7, ,4.8,
1、读出下列各数,并把它们填在相应的圈里:
正数
负数
,+73,4.8,
-11,-2.7,
-11,-2.7,-
自学检测1(3分钟)
2、判断:0
(1)一个数的前面不带有负号,这个数就是正数。( )
(2)0℃表示没有温度。 ( )
(3)零既不是正数,也不是负数。 ( )
√
×
×
既不是正数也
不是负数
0
自学检测1(3分钟)
3、小丽说:“一个数,如果不是正数,必定就是负数。”你认为她说的对吗?为什么?
解:不对,0既不是正数也不是负数。
不是正数的数是0或负数
不是负数的数是0或正数
非负数
非正数
4.下列语句正确的是 ( )
A.0℃表示没有温度
B.0表示什么也没有
C.0是非正数
D.0既可以看作是正数又可以看作是负数
C
变式训练.下列语句正确的有 ( )
①0常用来表示某些量的基准数
②0只表示什么也没有
③0是整数
④0是正数和负数的分界点
⑤0是非正数
A.1个 B.2个 C.3个 D.4个
D
笔记
1.如何区分一个数是正数还是负数
首先找0,然后看性质符号;
不含“+”“-”号,或者只含“+”号,
或者“-”号的个数是偶数则为正数。否则为负数。
知识点拨
0只表示没有吗
1.空罐中的金币数量0个;2.温度中的0℃;
3.海平面的高度0m;4.标准水位0m;
5.身高比较的基准0m; ……
0是正负数的分界点.它不再简简单单的只表示没有,它具有丰富的意义,如
0可以用来表示基准,一般地,高于基准的量用正数表示,低于基准的量用负数表示
2.
阅读课本P3例题,完成以下任务:
1、举出几对具有相反意义的量。
2、说说如何用正负数表示具有相反意义的量?
3、若选定150cm作为标准,你的身高表示为多少?
4、完成课本P3的练习。
自学指导2(5分钟)
零上 与零下
盈利 与亏损
加分 与扣分
高出 与低于
向东 与向西
具有相反意义
具有相反意义:上升与下降、增与减、收入与支出、胜与负、进与退、多与少、盈利与亏损、向东与向西、顺与逆、过剩与不足、重与轻等
如果有两个量是同类量,但表示的意义相反,那么这两个量就叫做具有相反意义的量
100C
40C
8元 5元
10分 15分
10米 5米
8米 4米
的量
1、具有相反意义的量。
什么是具有相反意义的量?
成对出现
用正数和负数可以表示同一个问题中具有相反意义的量
在具有相反意义的两个量中,任意规定其中一个量用正数表示,那么与这个量意义相反的量就用负数来表示。注意基准,一般基准是0.
例如:把上涨3.6%记为+3.6%,
那么下跌0.6%记作-0.6%
读作:正3.6%
读作:负0.6%
2、如何用正负数表示同一个问题中具有相反意义的量?
意义相反,有数量,同类量
一般规定:按指定方向变化的用正数表示
3、若选定150cm作为标准,你的身高表示为多少?
4、课本P3的练习答案
1、解:规定增加记为“+”,减少记为“-”,则:2010年为+108.7mm; 2009年为-81.5 mm; 2008年为+53.5 mm.
2.解:这个物体又移动了-1 m表示物体向左移动了1m这时物体又回到了原来的位置.
1、下列语句正确的是( )
A、“黑色”和“白色”是具有相反意义的量。
B、盈利200元和出口300箱是具有相反意义的量。
C、“向北4.5米”和“向南4.5米”是具有相反意 义的量。
D、“+15米”就表示向东走了15米。
自学检测2 (7分钟)
C
2、下列各量可用正、负数来表示的是( )
A、向北走3千米,向东走3千米。
B、甲班有男生25人,女生20人。
C、上午气温零上29℃,下午气温零上18℃.
D、上升200米,下降150米。
D
3、数学考试85分以上为优秀,老师将某一小组
的四名学生的数学分数以85分为标准,分别记
作:+10,-5,0,+15,则这四名同学的实际
成绩分别是______; _____; ______ ;______。
4、在某次乒乓球质量检测中,一只乒乓球超出
标准质量0.02克记作+0.02克,那么-0.03克
表示 ___________________。
95分
80分
85分
100分
轻于标准质量0.03克
5正负数表示的意义
(1)如果收入 120元记作+120元,那么-70元表示__________;
(2)如果蚂蚁向上爬 30 cm记作+30 cm,那么-10 cm表示_________________________;
(3)温度下降-5 ℃表示__________________;
(4)体重增加-3 kg表示__________________.
6、说出下列语句的实际意义
(1)小刚向西走了-100米;
(2)指针按顺时针旋转了-30°
解:小刚向东走了100米
解:指针按逆时针旋转了30 °
学生讨论、更正,教师点拨。
。
小结(2分钟)
你这节课学到了什么?
1、理解正数、负数的概念;会区分一个数是正数还是负数;
2、用正负数表示同一个问题中相反意义的量 (中考考点3分);
3、负数和0的意义。
注意:有的要带单位
1、如果水位升高3m时水位变化记作+3m,那么水位下降3m时水位变化记作( )
A. -3m B.3m C.6m D.-6m
A
2、(变式)如果收入80元记作+80元,那么支出记作( )
A. +20元 B. -20元 C. +100元 D. -100元
B
3.(1)东、西为两个相反方向,如果-4米表示一个物体向西运动4米,那么+2米表示____________,物体原地不动记作________;
(2)某仓库运进面粉7.5吨记为+7.5吨,那么运出3.8吨应记作_________。
向东运动2米
0米
-3.8吨
当堂训练:(15分钟)
(3)如果中午12时记作0时,下午3时记作+3时,上午9时记作 。
-3时
4、 如若把警戒水位定为0 m,水位高于警戒水位1.6m记
作_______ ,水位低于警戒水位0.2m时,记作 ;
+1.6m
-0.2m
5、(变式)南京长江大桥桥头堡的顶端高出地面约70米,
可记作 ,桥头堡的地基打入地下约30米深
的岩层,可记作
+70m
-30m
6、在有理数-3,0,23,-85,3.7中,属于非负数的个数有( )
A.4个 B.3个 C.2个 D.1个
B
7、某市某一天的最高温度是零上5℃,最低温度是零下5℃。如何表示这一天的最高气温和最低气温?
8、(变式)珠穆朗玛峰高于海平面8848米,吐鲁番盆地低于海平面155米,“高于”和“低于”其意义是相反的。如何表示它们的高度?
解:最高气温: 5℃;最低气温:- 5℃
解:珠穆朗玛峰高8848m;吐鲁番盆地-155m
正数:___________________________
负数:___________________________
既不是正数,也不是负数:________________
9、将下列各数按要求分别填入相应的横线上:
板书
1、正数、负数的概念;
2、区分一个数是正数还是负数
首先找0,然后看符号;不含“+”“-”号,或者只含“+”号,或者“-”号的个数是偶数则为正数。否则为负数。
2、用正负数表示同一个问题中相反意义的量 (中考考点3分);
3、0的意义。
注意:有的要带单位
10、(选做题)找规律:
(1)1,-2,3,-4,5,-6,7,-8 ,……其中第199个数为 _____ ,第2002个数_____ ,规律是_ _____________;
(2)1,2,-3,4,5,-6,7,8 ,-9 ……
其中第345个数为 _____ ,第2002个数_____ ,
规律是 _______ _______ ;
(3)-1,2,-3,4,-5,6,-7,8 ,-9……其中第279个数为 _____ ,第320个数的符号为___,规律是___ ___________;
199
-2002
奇数为+,偶数为-
-345
2002
3的倍数为-,其它为+
-279
+
奇数为-,偶数为+
数阵找规律和图形找规律
题型:
技巧:
标序列号和提公因式
找规律法就是从给出的特殊量中寻找其一般规律的方法,对于按照一定的顺序给出的一系列量,我们要根据已知的量找出其一般排列规律,通常可采用标序列号法找规律。
比较给出的数和序列号变化情况:1.符号变化情况、 2.数字变化情况,就很容易找出其变化规律.符号及数字与位置数之间的关系:
1.奇数位置上的数的符号为“一”,偶数位置上的数的符号为“+”(奇负偶正)
2.各个位置上的数(不考虑符号) 位置数的关系式 。
