2022-2023学年人教版数学九年级上册23.1 图形的旋转 导学案(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册23.1 图形的旋转 导学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 221.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 00:00:00 | ||
图片预览


文档简介
23.1图形的旋转
【学习目标】
1.了解旋转及其旋转中心和旋转角的概念和性质。
2.了解旋转对应点的概念及应用它们解决一些实际问题。
【学习重点】
旋转及对应点的有关概念及其应用。
【学习难点】
从生活中抽象出数学概念。
【学习过程】
一、引入。
请同学们完成下面各题。
(1)将如图所示的四边形ABCD平移,使点B的对应点为点D,作出平移后的图形。
(2)如图,已知△ABC和直线l,请你画出△ABC关于l的对称图形△A′B′C′。
(3)①圆是轴对称图形吗?②等腰三角形呢?③你还能指出其他的吗?
二、预习导学。
1.什么叫图形的旋转?什么是旋转中心、旋转角和对应角?
2.观察:让学生看转动的钟表和风车等。
(1)上面情景中的转动现象,有什么共同的特征?(指针、风车叶片分别绕中间点旋转)
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?(形状、大小不变,位置发生变化)
3.问题:
(1)从3时到5时,时针转动了多少度?(60°)
(2)风车每片叶轮转到与下一片原来的位置重合时,风车旋转了多少度?(60°)
(3)以上现象有什么共同特点?(物体绕固定点旋转)
思考:在数学中如何定义旋转?
4.旋转的性质:
(1)对应点到旋转中心的距离_____。
(2)对应点与旋转中心所连线段的夹角等于_____。
(3)旋转前、后的图形_____。
5.归纳:
把一个图形绕着某一点O转动一个角度的图形变换叫做旋转,点O叫做旋转中心,转动的角叫做旋转角。如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点。选择不同的旋转中心、不同的旋转角旋转同一个图案,会出现不同的效果。
三、检测
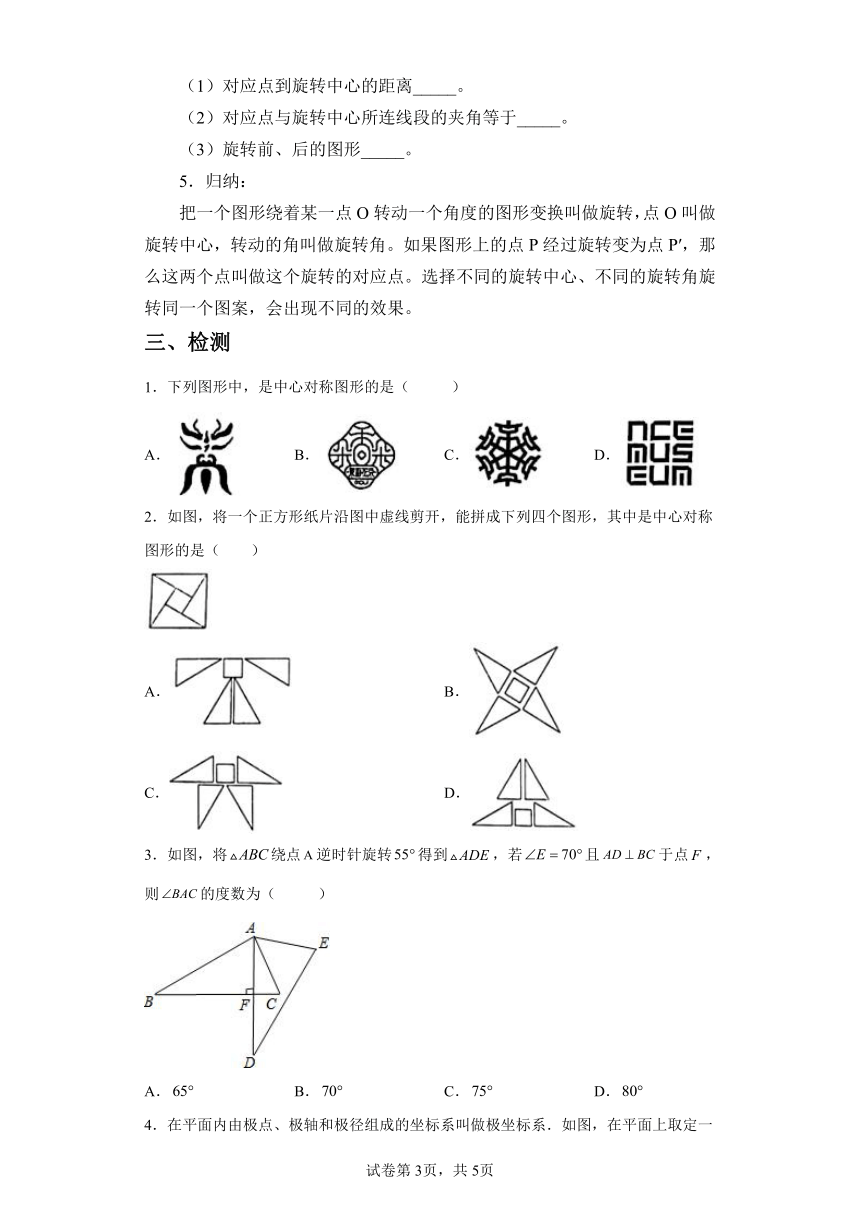
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.如图,将一个正方形纸片沿图中虚线剪开,能拼成下列四个图形,其中是中心对称图形的是( )
A. B.
C. D.
3.如图,将绕点逆时针旋转得到,若且于点,则的度数为( )
A. B. C. D.
4.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A. B. C. D.
5.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )
A. B.4 C. D.5
6.一个正五角星绕着它的中心至少旋转_________度能与自身重合.
7.如图,将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α(0<α<180°)得到△AB'C′,使得点B′、A、C在同一条直线上,则α等于_____°.
8.如图,在平面直角坐标系中,一次函数的图像分别交、轴于点、,将直线绕点按顺时针方向旋转,交轴于点,则直线的函数表达式是__________.
9.如图,将绕直角顶点按逆时针方向旋转得到.已知,求的度数.
10.如图,点在射线上,.如果绕点按逆时针方向旋转到,那么点的位置可以用表示.
按上述表示方法,若,,则点的位置可以表示为
11.在《折叠圆形纸片》综合实践课上,小东同学展示了如下的操作及问题:
(1)如图1,的半径为4cm,通过折叠圆形纸片,使得劣弧AB沿弦AB折叠后恰好过圆心,求AB长;
(2)如图2,弦AB,垂足为点C,劣弧AB沿弦AB折叠后经过的中点D,,求的半径.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
C2.B3.C4.B5.D
6.72
7.105°
10.(3,37°)
11.(1)cm
(2)cm
4 / 4
【学习目标】
1.了解旋转及其旋转中心和旋转角的概念和性质。
2.了解旋转对应点的概念及应用它们解决一些实际问题。
【学习重点】
旋转及对应点的有关概念及其应用。
【学习难点】
从生活中抽象出数学概念。
【学习过程】
一、引入。
请同学们完成下面各题。
(1)将如图所示的四边形ABCD平移,使点B的对应点为点D,作出平移后的图形。
(2)如图,已知△ABC和直线l,请你画出△ABC关于l的对称图形△A′B′C′。
(3)①圆是轴对称图形吗?②等腰三角形呢?③你还能指出其他的吗?
二、预习导学。
1.什么叫图形的旋转?什么是旋转中心、旋转角和对应角?
2.观察:让学生看转动的钟表和风车等。
(1)上面情景中的转动现象,有什么共同的特征?(指针、风车叶片分别绕中间点旋转)
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?(形状、大小不变,位置发生变化)
3.问题:
(1)从3时到5时,时针转动了多少度?(60°)
(2)风车每片叶轮转到与下一片原来的位置重合时,风车旋转了多少度?(60°)
(3)以上现象有什么共同特点?(物体绕固定点旋转)
思考:在数学中如何定义旋转?
4.旋转的性质:
(1)对应点到旋转中心的距离_____。
(2)对应点与旋转中心所连线段的夹角等于_____。
(3)旋转前、后的图形_____。
5.归纳:
把一个图形绕着某一点O转动一个角度的图形变换叫做旋转,点O叫做旋转中心,转动的角叫做旋转角。如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点。选择不同的旋转中心、不同的旋转角旋转同一个图案,会出现不同的效果。
三、检测
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.如图,将一个正方形纸片沿图中虚线剪开,能拼成下列四个图形,其中是中心对称图形的是( )
A. B.
C. D.
3.如图,将绕点逆时针旋转得到,若且于点,则的度数为( )
A. B. C. D.
4.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A. B. C. D.
5.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )
A. B.4 C. D.5
6.一个正五角星绕着它的中心至少旋转_________度能与自身重合.
7.如图,将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α(0<α<180°)得到△AB'C′,使得点B′、A、C在同一条直线上,则α等于_____°.
8.如图,在平面直角坐标系中,一次函数的图像分别交、轴于点、,将直线绕点按顺时针方向旋转,交轴于点,则直线的函数表达式是__________.
9.如图,将绕直角顶点按逆时针方向旋转得到.已知,求的度数.
10.如图,点在射线上,.如果绕点按逆时针方向旋转到,那么点的位置可以用表示.
按上述表示方法,若,,则点的位置可以表示为
11.在《折叠圆形纸片》综合实践课上,小东同学展示了如下的操作及问题:
(1)如图1,的半径为4cm,通过折叠圆形纸片,使得劣弧AB沿弦AB折叠后恰好过圆心,求AB长;
(2)如图2,弦AB,垂足为点C,劣弧AB沿弦AB折叠后经过的中点D,,求的半径.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
C2.B3.C4.B5.D
6.72
7.105°
10.(3,37°)
11.(1)cm
(2)cm
4 / 4
同课章节目录
