14.1.1同底数幂的乘法
图片预览






文档简介
课件19张PPT。 14.1.1
同底数幂的乘法学习目标
1.理解同底数幂的乘法法则
2.运用同底数幂的乘法法则解决一些实际问题
学习重点
正确理解同底数幂的乘法法则
学习难点
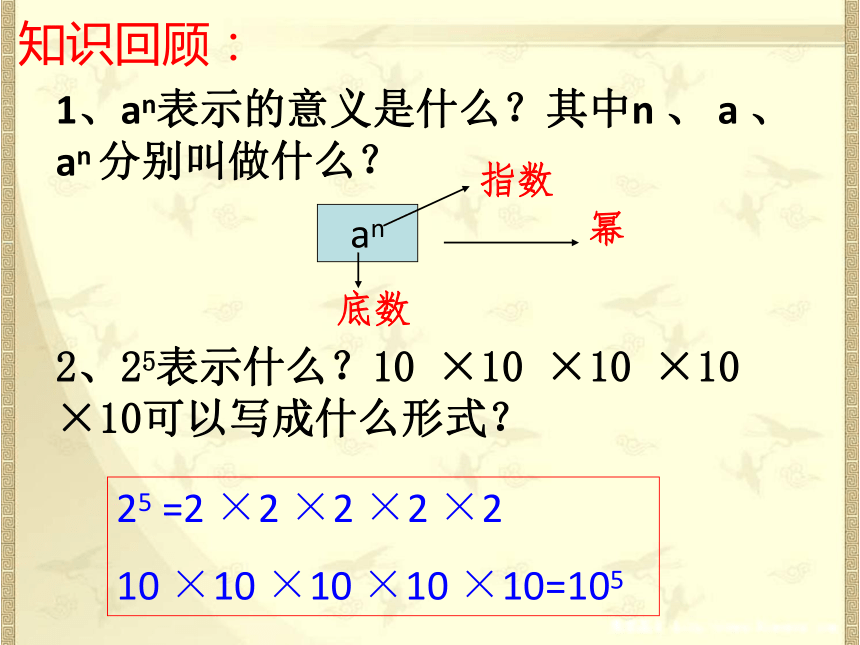
正确理解和应用同底数幂的乘法法则 “神州号”宇宙飞船载人航天飞行是我国航天事业的伟大壮举。它飞行的速度约为104米/秒,每天飞行时间约为105秒。它每天约飞行了多少米?104×105同底数幂相乘1、an表示的意义是什么?其中n 、 a 、 an 分别叫做什么?an指数底数幂2、25表示什么?10 ×10 ×10 ×10 ×10可以写成什么形式?25 =2 ×2 ×2 ×2 ×2
10 ×10 ×10 ×10 ×10=105知识回顾:(2)10×10×10×10可以写成____;(3) a的底数是__,指数是__;2×2×2×2×2a1a+b3-2424热身练习式子103×102的意义是什么? 思考:103与102 的积 底数相同 这个式子中的两个因式有何特点?请同学们先根据自己的理解,解答下列各题.
103 ×102 =(10×10×10)×(10×10) = 10( )
23 ×22 = =2( )
5(2×2×2)×(2×2)5 a3×a2 = = a( ) .5(a a a)(a a)=2×2×2×2×2= a a a a a3个a2个a5个a合作探究 根据乘方的意义填空,看看计算结果有什么规律?(1)
(2)
(3)
75m+n猜想: am · an= am+n (当m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a即am · an = am+n (当m、n都是正整数)(aa…a)(aa…a)(乘方的意义)(乘法结合律)(乘方的意义)am · an = am+n (当m、n都是正整数)同底数幂相乘,想一想: 当三个或三个以上同底数幂相乘时,是否也 ? 具有这一性质呢? 怎样用公式表示?底数 ,指数 。不变相加 同底数幂的乘法性质: 请你尝试用文字概括这个结论。 我们可以直接利用它进行计算.如 43×45=43+5=48 如 am·an·ap = am+n+p (m、n、p都是正整数)运算形式运算方法(同底、乘法) (底不变、指加法) 幂的底数必须相同,
相乘时指数才能相加.慧眼识金 下列是同底数幂的是( )
A
B
C
Dc准确判断
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3 b5 · b5= b10 b5 + b5 = 2b5 x5 · x5 = x10 y5 · y5 =y10 c · c3 = c4× × × ×××尝试反馈,理解新知例1
(1)x2×x5 (2) 107×104
(3) 5m×5n(m、n都是正整数) (4) xm×x 3m+1解: (1)x2×x5=x 2+5=x7(2) 107×104 =a 7+4=a11(4)xm.x 3 m+1=x m+3m+1=x 4m+1(3)5m×5n=5 m+n例2(1)23 × 24 × 25(2)y.y2.y3=23+4+5
=212=y1+2+3
=y6挑战自己:快速抢答:
??计算:(1011 )( a10 )( x10 )( b8 )(2) a7 ·a3(3) x5 ·x5 (4) b5 · b ·b2(1) 105×1061.填空:(1)若am=a3?a4,则m=____(2)若x4?xm=x6,则m=____(3)若x?x2?x3?x4?x5=xm, 则m=____7215变式训练2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .35623 23 3253622 × = 33 32 × ×=能力挑战如果xm-n·x2n+1=xn,且ym-1·y4-n=y7.
求m和n的值.m=―1,n=―5今天,你有何收获? am · an = am+n (m、n为正整数)
小结:同底数幂相乘,底数不变,指数相加。同底数幂的乘法:同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)我学到了什么?知识 方法 “特殊→一般→特殊”
例子 公式 应用不变,相加.再
见
同底数幂的乘法学习目标
1.理解同底数幂的乘法法则
2.运用同底数幂的乘法法则解决一些实际问题
学习重点
正确理解同底数幂的乘法法则
学习难点
正确理解和应用同底数幂的乘法法则 “神州号”宇宙飞船载人航天飞行是我国航天事业的伟大壮举。它飞行的速度约为104米/秒,每天飞行时间约为105秒。它每天约飞行了多少米?104×105同底数幂相乘1、an表示的意义是什么?其中n 、 a 、 an 分别叫做什么?an指数底数幂2、25表示什么?10 ×10 ×10 ×10 ×10可以写成什么形式?25 =2 ×2 ×2 ×2 ×2
10 ×10 ×10 ×10 ×10=105知识回顾:(2)10×10×10×10可以写成____;(3) a的底数是__,指数是__;2×2×2×2×2a1a+b3-2424热身练习式子103×102的意义是什么? 思考:103与102 的积 底数相同 这个式子中的两个因式有何特点?请同学们先根据自己的理解,解答下列各题.
103 ×102 =(10×10×10)×(10×10) = 10( )
23 ×22 = =2( )
5(2×2×2)×(2×2)5 a3×a2 = = a( ) .5(a a a)(a a)=2×2×2×2×2= a a a a a3个a2个a5个a合作探究 根据乘方的意义填空,看看计算结果有什么规律?(1)
(2)
(3)
75m+n猜想: am · an= am+n (当m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a即am · an = am+n (当m、n都是正整数)(aa…a)(aa…a)(乘方的意义)(乘法结合律)(乘方的意义)am · an = am+n (当m、n都是正整数)同底数幂相乘,想一想: 当三个或三个以上同底数幂相乘时,是否也 ? 具有这一性质呢? 怎样用公式表示?底数 ,指数 。不变相加 同底数幂的乘法性质: 请你尝试用文字概括这个结论。 我们可以直接利用它进行计算.如 43×45=43+5=48 如 am·an·ap = am+n+p (m、n、p都是正整数)运算形式运算方法(同底、乘法) (底不变、指加法) 幂的底数必须相同,
相乘时指数才能相加.慧眼识金 下列是同底数幂的是( )
A
B
C
Dc准确判断
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3 b5 · b5= b10 b5 + b5 = 2b5 x5 · x5 = x10 y5 · y5 =y10 c · c3 = c4× × × ×××尝试反馈,理解新知例1
(1)x2×x5 (2) 107×104
(3) 5m×5n(m、n都是正整数) (4) xm×x 3m+1解: (1)x2×x5=x 2+5=x7(2) 107×104 =a 7+4=a11(4)xm.x 3 m+1=x m+3m+1=x 4m+1(3)5m×5n=5 m+n例2(1)23 × 24 × 25(2)y.y2.y3=23+4+5
=212=y1+2+3
=y6挑战自己:快速抢答:
??计算:(1011 )( a10 )( x10 )( b8 )(2) a7 ·a3(3) x5 ·x5 (4) b5 · b ·b2(1) 105×1061.填空:(1)若am=a3?a4,则m=____(2)若x4?xm=x6,则m=____(3)若x?x2?x3?x4?x5=xm, 则m=____7215变式训练2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .35623 23 3253622 × = 33 32 × ×=能力挑战如果xm-n·x2n+1=xn,且ym-1·y4-n=y7.
求m和n的值.m=―1,n=―5今天,你有何收获? am · an = am+n (m、n为正整数)
小结:同底数幂相乘,底数不变,指数相加。同底数幂的乘法:同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)我学到了什么?知识 方法 “特殊→一般→特殊”
例子 公式 应用不变,相加.再
见
