14.2.1 平方差公式
文档属性
| 名称 | 14.2.1 平方差公式 |  | |
| 格式 | zip | ||
| 文件大小 | 300.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-02 15:47:03 | ||
图片预览






文档简介
课件17张PPT。14.2 乘法公式
1 .平方差公式学习目标:
1、会推导平方差公式,并且懂得运用平方差公式进行简单计算.
2、经历探索特殊形式的多项式乘法的过程,发展符号感和推理能力,使学生逐渐掌握平方差公式.
学习重点:
平方差公式的推导和运用,以及对平方差公式的几何背景的了解.
学习难点:
平方差公式的应用. (x + 3)( x+5)=x2+5x+3X+15=x2+8x多项式与多项式是如何相乘的?+15 (a+b)(m+n)=am+an+bm+bn①(x + 4)( x-4)
②(1 + 2a)( 1-2a)
③(m+ 6n)( m-6n)
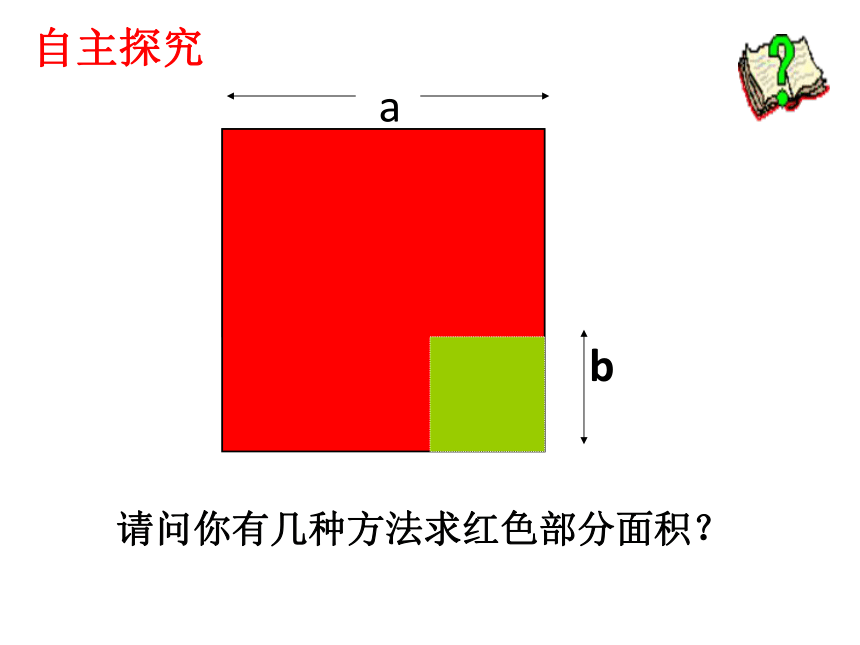
④(5y + z)(5y-z)计算下列各题算一算,比一比,看谁算得又快又准 ②(1 + 2a)( 1-2a)=1 -4a2③(m+ 6n)( m-6n)=m2 - 36n2④(5y + z)(5y-z)= 25y2 - z2①(x + 4)( x-4)=x2 - 16它们的结果有什么特点?x2 - 4212-(2a)2m2 - (6n)2(5y)2 - z2探 究 平方差公式 证明:(a+b)(a-b) 两数和与这两数差的积,等于它们的平方差.(多项式乘法法则)(合并同类项)注:这里的a、b可以是两个单项式,也可以是两个多项式.探 究请问你有几种方法求红色部分面积?自主探究?
?
长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
abb自主探究例1 运用平方差公式计算:
(1) (3x+2) (3x-2); (2) (b+2a)(2a-b); (3) (-x+2y) (-x-2y).分析:在(1)中,可以把3x看成a,2看成b,即
(3x+2) (3x - 2) = (3x)2 - 22
(a + b) (a - b) = a2 - b2解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.(2) (b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2(3)(-x+2y)(-x-2y)
= (-x)2-(2y)2
=x2-4y2.典例分析(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 拓 展 练 习典例分析例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98
=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.知难而进1.计算 20042 - 2003×2005;解:
20042 - 2003×2005= 20042 - (2004-1)(2004+1)= 20042- (20042-12 )= 20042- 20042+12 =1(1)(a+3b)(a - 3b)=4 a2-9;=4x4-y2.=(2a+3)(2a-3)=a2-9b2 ;=(2a)2-32 =(-2x2 )2-y2 =(50+1)(50-1)=502-12 =2500-1=2499=(9x2-16) -(6x2+5x -6)=3x2-5x- 10=(a)2-(3b)2 (2)(3+2a)(-3+2a)(3)51×49(5)(3x+4)(3x-4)-(2x+3)(3x-2)(4)(-2x2-y)(-2x2+y)利用平方差公式计算:巩 固 练 习例3:利用平方差公式计算:(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
典例分析:试一试: ( ) (x4+y4)(x4+y4)(x4+y4)1.已知x2-y2=8,x-y=4,求x+y的值。
2.有两个正方形的周长之和为36cm,面积之差为72cm2,你能求出这两个正方形的边长吗?
3.(2+1)(22+1)(24+1)能否用平方差公式进行计算?如能,还需创造什么条件?
课堂练习 (a+b)(a-b)=(a)2-(b)2相反为b小结 相同为a 适当交换合理加括号平方差公式
1 .平方差公式学习目标:
1、会推导平方差公式,并且懂得运用平方差公式进行简单计算.
2、经历探索特殊形式的多项式乘法的过程,发展符号感和推理能力,使学生逐渐掌握平方差公式.
学习重点:
平方差公式的推导和运用,以及对平方差公式的几何背景的了解.
学习难点:
平方差公式的应用. (x + 3)( x+5)=x2+5x+3X+15=x2+8x多项式与多项式是如何相乘的?+15 (a+b)(m+n)=am+an+bm+bn①(x + 4)( x-4)
②(1 + 2a)( 1-2a)
③(m+ 6n)( m-6n)
④(5y + z)(5y-z)计算下列各题算一算,比一比,看谁算得又快又准 ②(1 + 2a)( 1-2a)=1 -4a2③(m+ 6n)( m-6n)=m2 - 36n2④(5y + z)(5y-z)= 25y2 - z2①(x + 4)( x-4)=x2 - 16它们的结果有什么特点?x2 - 4212-(2a)2m2 - (6n)2(5y)2 - z2探 究 平方差公式 证明:(a+b)(a-b) 两数和与这两数差的积,等于它们的平方差.(多项式乘法法则)(合并同类项)注:这里的a、b可以是两个单项式,也可以是两个多项式.探 究请问你有几种方法求红色部分面积?自主探究?
?
长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
abb自主探究例1 运用平方差公式计算:
(1) (3x+2) (3x-2); (2) (b+2a)(2a-b); (3) (-x+2y) (-x-2y).分析:在(1)中,可以把3x看成a,2看成b,即
(3x+2) (3x - 2) = (3x)2 - 22
(a + b) (a - b) = a2 - b2解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.(2) (b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2(3)(-x+2y)(-x-2y)
= (-x)2-(2y)2
=x2-4y2.典例分析(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 拓 展 练 习典例分析例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98
=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.知难而进1.计算 20042 - 2003×2005;解:
20042 - 2003×2005= 20042 - (2004-1)(2004+1)= 20042- (20042-12 )= 20042- 20042+12 =1(1)(a+3b)(a - 3b)=4 a2-9;=4x4-y2.=(2a+3)(2a-3)=a2-9b2 ;=(2a)2-32 =(-2x2 )2-y2 =(50+1)(50-1)=502-12 =2500-1=2499=(9x2-16) -(6x2+5x -6)=3x2-5x- 10=(a)2-(3b)2 (2)(3+2a)(-3+2a)(3)51×49(5)(3x+4)(3x-4)-(2x+3)(3x-2)(4)(-2x2-y)(-2x2+y)利用平方差公式计算:巩 固 练 习例3:利用平方差公式计算:(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
典例分析:试一试: ( ) (x4+y4)(x4+y4)(x4+y4)1.已知x2-y2=8,x-y=4,求x+y的值。
2.有两个正方形的周长之和为36cm,面积之差为72cm2,你能求出这两个正方形的边长吗?
3.(2+1)(22+1)(24+1)能否用平方差公式进行计算?如能,还需创造什么条件?
课堂练习 (a+b)(a-b)=(a)2-(b)2相反为b小结 相同为a 适当交换合理加括号平方差公式
