14.3.1提公因式法分解因式
文档属性
| 名称 | 14.3.1提公因式法分解因式 |  | |
| 格式 | zip | ||
| 文件大小 | 487.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-02 15:47:58 | ||
图片预览






文档简介
课件15张PPT。14.3.1
提公因式法分解因式学习目标:
1、经历逆向得出因式分解方法的过程,并会用提公因式法分解因式.
2、发展学生逆向思考问题的能力和推理能力.
3、在学习过程中获得成功的体验,建立自信心.
学习重点:
掌握公因式的概念,会使用提公因式法进行因式分解.
学习难点:
正确找出公因式,正确用提公因式法把多项式进行因式分解.
请把下列多项式写成整式的乘积的形式:
(1)x2+x=___________;
(2)x2 – 1=__________ .x(x+1)(x+1)(x-1) 上面我们把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.探究a2-b2=(a+b)2=m(a+b)(a+b)(a-b)(a+b)2m(a+b)=a2-b2=a2+2ab+b2 =am+bm整式的积多项式多项式整式的积a2+2ab+b2am+bm因式分解与整式乘法是互逆过程因式分解与整式乘法的关系:=(a+b)(a-b)练习一 理解概念判断下列各式哪些是整式乘法?哪些是因式分解?
(1) x2-4y2=(x+2y)(x-2y);
(2) 2x(x-3y)=2x2-6xy
(3) (5a-1)2=25a2-10a+1 ;
(4) x2+4x+4=(x+2)2 ;
(5) (a-3)(a+3)=a2-9
(6) m2-4=(m+2)(m-2) ;
(7) 2πR+ 2πr= 2π(R+r).因式分解整式乘法整式乘法因式分解整式乘法因式分解因式分解 多项式中各项都含有的相同因式,叫做这个多项式的公因式。相同因式m这个多项式有什么特点?由m(a+b+c) = ma+mb+mc可得: ma+mb+mc =m(a+b+c) 像这样就把ma+mb+mc分解成两个因式乘积的形式,其中一个因式是各项的公因式m,另一个因式(a+b+c)是ma+mb+mc除以 m所得的商,像这种分解因式的方法叫做
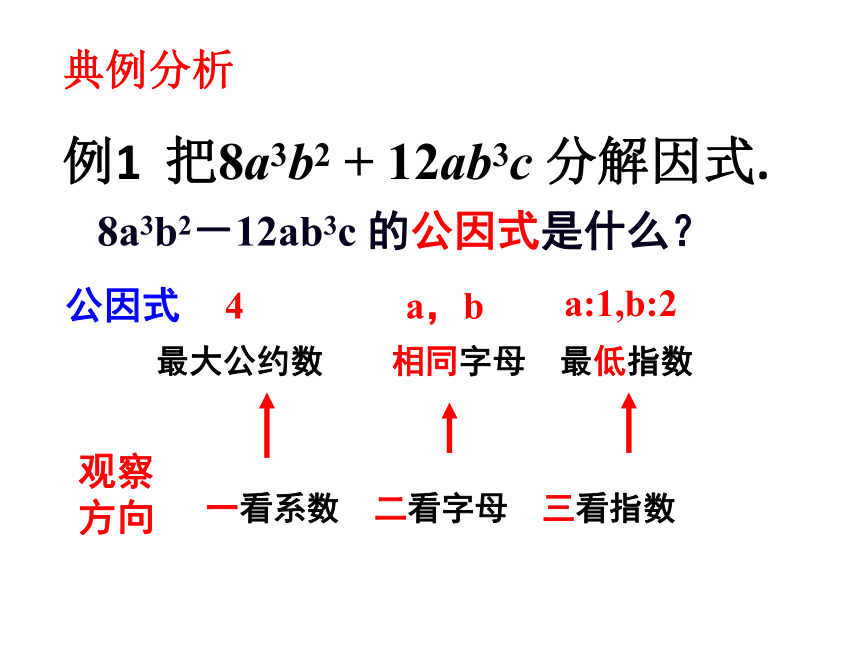
提公因式法.探 究8a3b2-12ab3c 的公因式是什么?公因式4a,ba:1,b:2一看系数 二看字母 三看指数观察方向例1 把8a3b2 + 12ab3c 分解因式.典例分析提公因式后,另一个因式:
①项数应与原多项式的项数一样;
②不再含有公因式. 解:8a3b2+12ab3c
=4ab2·2a2+ 4ab2 ·3bc
= 4ab2 (2a2 + 3bc2)公因式: 4ab2典例分析例1 把8a3b2 + 12ab3c 分解因式. 注意:各项系数都是整数时,因式的系数应取各项系数的最大公约数;字母取各项的相同的字母,而且各字母的指数取次数最低的.(1)ma + mb ;
(2)4kx- 8ky ;
(3)5y3+20y2 ;
(4)a2b-2ab2+ab .m4k5y2ab试一试 说出下列多项式各项的公因式:并把多项式因式分解(a-2b +1)(y+4)(x - 2y)(a+b)例2 把2ac(b+2c)- (b+2c)分解因式. 解:2ac(b+2c) -(b+2c)
= (b+2c)(2ac-1) 公因式可以是数字、字母,也可以是单项式,还可以是多项式.典例分析1. 2x(x-2y)+4y(2y-x)
= 2x(x-2y)-4y(x-2y)
=2(x-2y)(x-2y)
=2(x-2y)2
练一练2.(2a+b)(3b-2a)-a(2a+b)
=(2a+b)(3b-2a-a)
=(2a+b)(3b-3a)
=3(2a+b)(b-a)试把下列各式分解因式1.找出下列各多项式的公因式,并尝试将各多
项式因式分解.
(1)3x+9;
(2)7x2-28xy;
(3)8a3b2-12ab3c+2ab;
(4)6ax2-9axy+3a.课堂练习=3(x+3)=7x·x-7x·4y=7x(x-4y)=2ab·4a2b-2ab·6b2c+2ab·1 =2ab(4a2b-6b2c+1)=3a·2x2-3a·3xy+3a·1=3a(2x2-3xy+1)拓展与提高1.20042+2004能被2005整除吗? 提示:原式=2004(2004+1)=2004×2005分析:原式=(x+7)(4a2-3)
当a=-5,x=3时,原式=(3+7)[(-5)2-3]
=10×23=2302、确定公因式的方法:小 结3、提公因式法分解因式步骤(分两步):1、什么叫因式分解?(1)定系数 (2)定字母 (3)定指数第一步,找出公因式;
第二步,提取公因式.4、提公因式法分解因式应注意的问题:(1)公因式要提尽;(2)某想提出莫漏1;(3)提出负号时,要注意变号.再 见
提公因式法分解因式学习目标:
1、经历逆向得出因式分解方法的过程,并会用提公因式法分解因式.
2、发展学生逆向思考问题的能力和推理能力.
3、在学习过程中获得成功的体验,建立自信心.
学习重点:
掌握公因式的概念,会使用提公因式法进行因式分解.
学习难点:
正确找出公因式,正确用提公因式法把多项式进行因式分解.
请把下列多项式写成整式的乘积的形式:
(1)x2+x=___________;
(2)x2 – 1=__________ .x(x+1)(x+1)(x-1) 上面我们把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.探究a2-b2=(a+b)2=m(a+b)(a+b)(a-b)(a+b)2m(a+b)=a2-b2=a2+2ab+b2 =am+bm整式的积多项式多项式整式的积a2+2ab+b2am+bm因式分解与整式乘法是互逆过程因式分解与整式乘法的关系:=(a+b)(a-b)练习一 理解概念判断下列各式哪些是整式乘法?哪些是因式分解?
(1) x2-4y2=(x+2y)(x-2y);
(2) 2x(x-3y)=2x2-6xy
(3) (5a-1)2=25a2-10a+1 ;
(4) x2+4x+4=(x+2)2 ;
(5) (a-3)(a+3)=a2-9
(6) m2-4=(m+2)(m-2) ;
(7) 2πR+ 2πr= 2π(R+r).因式分解整式乘法整式乘法因式分解整式乘法因式分解因式分解 多项式中各项都含有的相同因式,叫做这个多项式的公因式。相同因式m这个多项式有什么特点?由m(a+b+c) = ma+mb+mc可得: ma+mb+mc =m(a+b+c) 像这样就把ma+mb+mc分解成两个因式乘积的形式,其中一个因式是各项的公因式m,另一个因式(a+b+c)是ma+mb+mc除以 m所得的商,像这种分解因式的方法叫做
提公因式法.探 究8a3b2-12ab3c 的公因式是什么?公因式4a,ba:1,b:2一看系数 二看字母 三看指数观察方向例1 把8a3b2 + 12ab3c 分解因式.典例分析提公因式后,另一个因式:
①项数应与原多项式的项数一样;
②不再含有公因式. 解:8a3b2+12ab3c
=4ab2·2a2+ 4ab2 ·3bc
= 4ab2 (2a2 + 3bc2)公因式: 4ab2典例分析例1 把8a3b2 + 12ab3c 分解因式. 注意:各项系数都是整数时,因式的系数应取各项系数的最大公约数;字母取各项的相同的字母,而且各字母的指数取次数最低的.(1)ma + mb ;
(2)4kx- 8ky ;
(3)5y3+20y2 ;
(4)a2b-2ab2+ab .m4k5y2ab试一试 说出下列多项式各项的公因式:并把多项式因式分解(a-2b +1)(y+4)(x - 2y)(a+b)例2 把2ac(b+2c)- (b+2c)分解因式. 解:2ac(b+2c) -(b+2c)
= (b+2c)(2ac-1) 公因式可以是数字、字母,也可以是单项式,还可以是多项式.典例分析1. 2x(x-2y)+4y(2y-x)
= 2x(x-2y)-4y(x-2y)
=2(x-2y)(x-2y)
=2(x-2y)2
练一练2.(2a+b)(3b-2a)-a(2a+b)
=(2a+b)(3b-2a-a)
=(2a+b)(3b-3a)
=3(2a+b)(b-a)试把下列各式分解因式1.找出下列各多项式的公因式,并尝试将各多
项式因式分解.
(1)3x+9;
(2)7x2-28xy;
(3)8a3b2-12ab3c+2ab;
(4)6ax2-9axy+3a.课堂练习=3(x+3)=7x·x-7x·4y=7x(x-4y)=2ab·4a2b-2ab·6b2c+2ab·1 =2ab(4a2b-6b2c+1)=3a·2x2-3a·3xy+3a·1=3a(2x2-3xy+1)拓展与提高1.20042+2004能被2005整除吗? 提示:原式=2004(2004+1)=2004×2005分析:原式=(x+7)(4a2-3)
当a=-5,x=3时,原式=(3+7)[(-5)2-3]
=10×23=2302、确定公因式的方法:小 结3、提公因式法分解因式步骤(分两步):1、什么叫因式分解?(1)定系数 (2)定字母 (3)定指数第一步,找出公因式;
第二步,提取公因式.4、提公因式法分解因式应注意的问题:(1)公因式要提尽;(2)某想提出莫漏1;(3)提出负号时,要注意变号.再 见
