21.1.2二次函数 y=ax^2+c 的图形和性质1 课件(共20张PPT)
文档属性
| 名称 | 21.1.2二次函数 y=ax^2+c 的图形和性质1 课件(共20张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-03 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
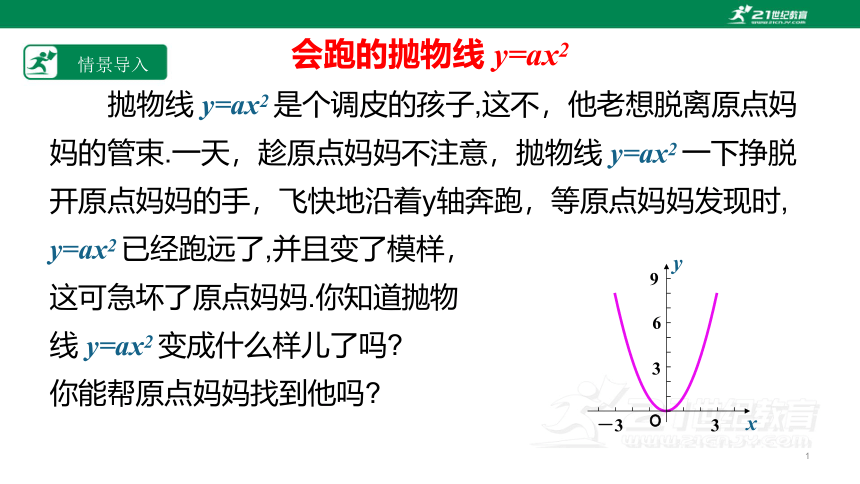
会跑的抛物线y=ax2抛物线y=ax2是个调皮的孩子,这不,他老想脱离原点妈妈的管束.一天,趁原点妈妈不注意,抛物线y=ax2一下挣脱开原点妈妈的手,飞快地沿着y轴奔跑,等原点妈妈发现时,y=ax2已经跑远了,并且变了模样,这可急坏了原点妈妈.你知道抛物线y=ax2变成什么样儿了吗 你能帮原点妈妈找到他吗 O-33369yx情景导入人教版九年级数学上册----二次函数y=ax +c的图形和性质22.1.3二次函数y=a(x-h) +k的图形和性质①学习目标
1.会作二次函数y=ax2 +k的图象,知道抛物线y=ax2 +k
与y=ax2的关系.
2.能利用y=ax2 +k 的图象得出其性质。
知识回顾
1.描点法画出二次函数的步骤:分别为 、 、______三个步骤.
2.二次函数y=ax2(a≠0)的图象是一条 ,
当a>0时,它的开口向 ,对称轴是 ,顶点坐标是 ;在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而____;当x=____时,y取最____值.
列表
描点
连线
当a<0时又会有什么变化呢?
抛物线
上
y轴
(0,0)
减小
增大
0
小
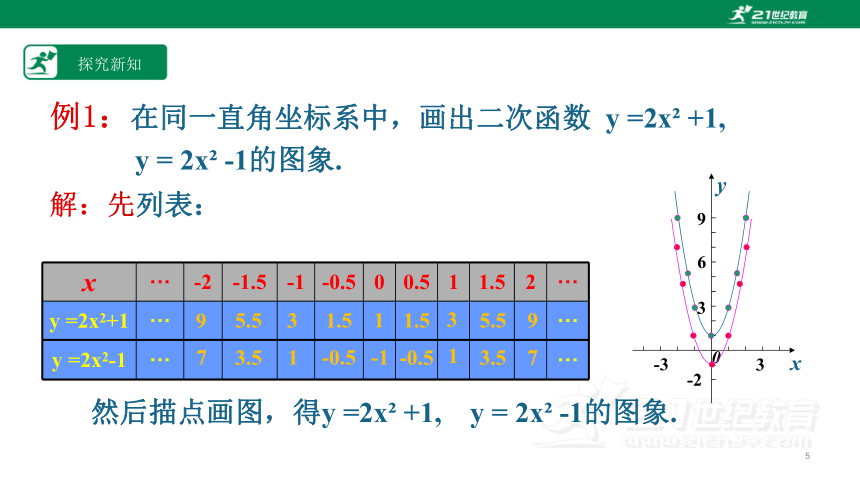
例1:在同一直角坐标系中,画出二次函数y =2x +1,y = 2x -1的图象.解:先列表:x···-2-1.5-1-0.500.511.52···y =2x2+1······y =2x2-1······1.511.5335.595.59-0.5-1-0.5113.573.57yx-33369-20然后描点画图,得y =2x +1, y = 2x -1的图象.探究新知探究新知
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2+1
y=2x2
y=2x2-1
二次函数
开口方向
顶点坐标
对称轴
向上
向上
(0,1)
(0,-1)
y轴
y轴
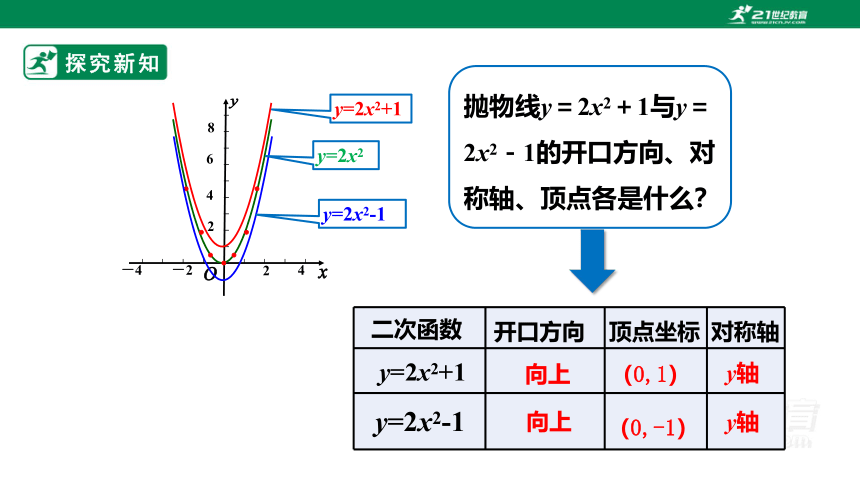
抛物线y=2x2+1与y=2x2-1的开口方向、对称轴、顶点各是什么?
y=2x2+1
y=2x2-1
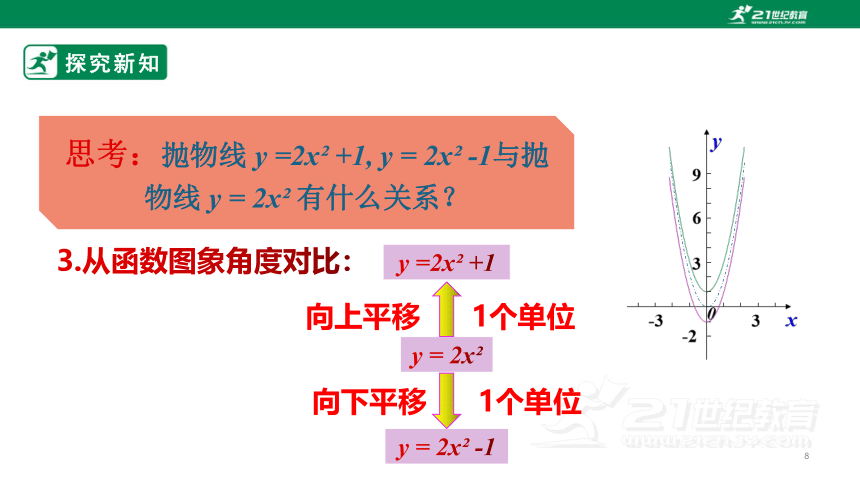
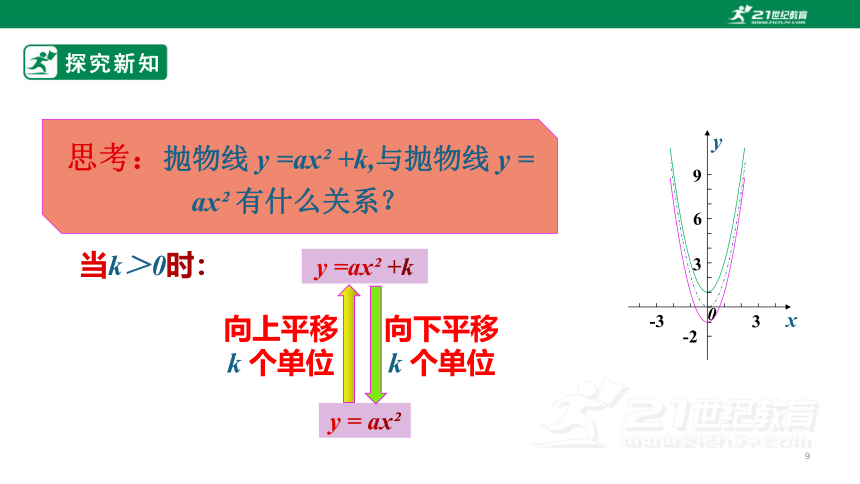
探究新知思考:抛物线y =2x +1, y = 2x -1与抛物线y = 2x 有什么关系?x···-2-1.5-1-0.500.511.52···y =2x2+1······y =2x2······y =2x2-1······1.511.5335.595.59-0.5-1-0.5113.573.570.500.5224.584.582.从函数对应值表格角度对比:1.从函数解析式角度对比:探究新知思考:抛物线y =2x +1, y = 2x -1与抛物线y = 2x 有什么关系?向上平移1个单位y = 2x -1y =2x +1y = 2x 向下平移1个单位3.从函数图象角度对比:探究新知思考:抛物线y =ax +k,与抛物线y = ax 有什么关系?yx-33369-20向上平移k个单位y =ax +ky = ax 向下平移k个单位当k>0时:探究新知思考:抛物线y =ax +k,与抛物线y = ax 有什么关系?yx-33369-20向下平移∣k ∣个单位y =ax +ky = ax 向上平移∣k ∣个单位当k<0时:归纳总结y= ax +k(a≠0)图形开口方向顶点坐标对称轴增减性最值a>0a<0xyOOyx向上向下(0,k)y轴当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大.当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.当x=0时,抛物线有最低点y最小值=k当x=0时,抛物线有最高点y最大值=kxyOk>0k<0k>0k<0Oyx知识归纳
二次函数y=ax2+k的图象可由抛物线y=ax2的图象向上或向下平移____个单位长度得到.当k>0时,抛物线y=ax2向____平移____个单位长度得到抛物线y=ax2+k;当k<0时,抛物线y=ax2向____平移____个单位长度得到抛物线y=ax2+k.
y=ax2+k
当向下平移k时
y=ax2-k
当向上平移 k 时
y=ax2
k>0
|k|
上
k
下
-k
k<0
知识归纳
抛物线y=ax2与y=ax2+k的区别和联系:
函数解析式 顶点坐标 对称轴 开口方向 增减性
y=ax2(a≠0) (0,0) y轴 当a>0时,抛物线开口向上; 当a<0时,抛物线开口向下. 当a>0时,在对称轴左侧,y随x的增大而 ,在对称轴右侧,y随x的增大而 ____ ;当a<0时,在对称轴左侧,y随x的增大而 _____ ,在对称轴右侧,y随x的增大而____.
y=ax2+k(a≠0) (0,k) 减小
增大
增大
减小
例题讲解
例1
指出下列函数的开口方向、对称轴、顶点坐标及最值.
开口 方向 对称轴 顶点 坐标 最值
向上
向下
(0,4)
(0,-3)
y轴
y轴
当x=0时,有最大值y=4
当 x=0时,有最小值y=-3
例题讲解已知抛物线y=2x2-3.(3)若点 ( -4, y1), ( -1, y2) ,(2, y3)在抛物线y= 2x2-3上,则y1、y2、y3之间的大小关系为(用“<”连接).yx-3336-30y2<y3<y1y1y3y2例2学以致用
1.在同一平面直角坐标系中,不可能由函数 y=2x2+1 的图象通过上下平移变换得到的函数是( )
A.y=2x2- 1 B. y=2x2 C.y=2x2+7 D.y= x2+1
2.将抛物线 y=x2 向上平移1个单位,则平移后的抛物线的解析式为 .
3.抛物线 y=2x2-1 的顶点坐标为( )
A.(2,0) B.(2,1) C. (0,- 1) D. (0,1)
D
y=x2+1
C
学以致用
4.抛物线 y=x2+1 的最低点坐标为 ,
当 x 时,函数有最小值是 .
5.若二次函数 y=(3m-6)x2-1 的开口方向向下,则m的取值范
围是( )A.m> 2 B.m<2 C. m≠2 D. m>一2
6.把抛物线 y=ax2+c 向上平移2个单位,得到抛物线 y=x2,
则 a, c 的值分别是( )
A.1, 2 B.1,﹣2 C.﹣1, 2 D.﹣1,﹣2
(0,1)
=0
1
B
B
7.已知抛物线y=4x2+2上有两点A(x1,y1),B(x2,y2),且x1<x2<0,
则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.无法确定
C
课堂小结
a,k的符号 a>0,k>0 a>0,k<0 a<0,k>0 a<0,k<0
图象
开口方向 对称轴 顶点坐标 函数的增减性 最值 向上
向下
y轴(直线 x=0)
y轴(直线 x=0)
(0,k)
(0,k)
当 x<0 时,y 随 x 增大而减小;当 x>0 时,y 随 x 增大而增大.
当 x<0 时,y 随 x 增大而增大;当 x> 0时,y 随 x 增大而减小.
x=0时,y最小值=k
x=0时,y最大值=k
作业布置
1.教材P41习题22.1第5题(1);
2.见学生用书对应练习.
谢谢
会跑的抛物线y=ax2抛物线y=ax2是个调皮的孩子,这不,他老想脱离原点妈妈的管束.一天,趁原点妈妈不注意,抛物线y=ax2一下挣脱开原点妈妈的手,飞快地沿着y轴奔跑,等原点妈妈发现时,y=ax2已经跑远了,并且变了模样,这可急坏了原点妈妈.你知道抛物线y=ax2变成什么样儿了吗 你能帮原点妈妈找到他吗 O-33369yx情景导入人教版九年级数学上册----二次函数y=ax +c的图形和性质22.1.3二次函数y=a(x-h) +k的图形和性质①学习目标
1.会作二次函数y=ax2 +k的图象,知道抛物线y=ax2 +k
与y=ax2的关系.
2.能利用y=ax2 +k 的图象得出其性质。
知识回顾
1.描点法画出二次函数的步骤:分别为 、 、______三个步骤.
2.二次函数y=ax2(a≠0)的图象是一条 ,
当a>0时,它的开口向 ,对称轴是 ,顶点坐标是 ;在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而____;当x=____时,y取最____值.
列表
描点
连线
当a<0时又会有什么变化呢?
抛物线
上
y轴
(0,0)
减小
增大
0
小
例1:在同一直角坐标系中,画出二次函数y =2x +1,y = 2x -1的图象.解:先列表:x···-2-1.5-1-0.500.511.52···y =2x2+1······y =2x2-1······1.511.5335.595.59-0.5-1-0.5113.573.57yx-33369-20然后描点画图,得y =2x +1, y = 2x -1的图象.探究新知探究新知
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2+1
y=2x2
y=2x2-1
二次函数
开口方向
顶点坐标
对称轴
向上
向上
(0,1)
(0,-1)
y轴
y轴
抛物线y=2x2+1与y=2x2-1的开口方向、对称轴、顶点各是什么?
y=2x2+1
y=2x2-1
探究新知思考:抛物线y =2x +1, y = 2x -1与抛物线y = 2x 有什么关系?x···-2-1.5-1-0.500.511.52···y =2x2+1······y =2x2······y =2x2-1······1.511.5335.595.59-0.5-1-0.5113.573.570.500.5224.584.582.从函数对应值表格角度对比:1.从函数解析式角度对比:探究新知思考:抛物线y =2x +1, y = 2x -1与抛物线y = 2x 有什么关系?向上平移1个单位y = 2x -1y =2x +1y = 2x 向下平移1个单位3.从函数图象角度对比:探究新知思考:抛物线y =ax +k,与抛物线y = ax 有什么关系?yx-33369-20向上平移k个单位y =ax +ky = ax 向下平移k个单位当k>0时:探究新知思考:抛物线y =ax +k,与抛物线y = ax 有什么关系?yx-33369-20向下平移∣k ∣个单位y =ax +ky = ax 向上平移∣k ∣个单位当k<0时:归纳总结y= ax +k(a≠0)图形开口方向顶点坐标对称轴增减性最值a>0a<0xyOOyx向上向下(0,k)y轴当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大.当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.当x=0时,抛物线有最低点y最小值=k当x=0时,抛物线有最高点y最大值=kxyOk>0k<0k>0k<0Oyx知识归纳
二次函数y=ax2+k的图象可由抛物线y=ax2的图象向上或向下平移____个单位长度得到.当k>0时,抛物线y=ax2向____平移____个单位长度得到抛物线y=ax2+k;当k<0时,抛物线y=ax2向____平移____个单位长度得到抛物线y=ax2+k.
y=ax2+k
当向下平移k时
y=ax2-k
当向上平移 k 时
y=ax2
k>0
|k|
上
k
下
-k
k<0
知识归纳
抛物线y=ax2与y=ax2+k的区别和联系:
函数解析式 顶点坐标 对称轴 开口方向 增减性
y=ax2(a≠0) (0,0) y轴 当a>0时,抛物线开口向上; 当a<0时,抛物线开口向下. 当a>0时,在对称轴左侧,y随x的增大而 ,在对称轴右侧,y随x的增大而 ____ ;当a<0时,在对称轴左侧,y随x的增大而 _____ ,在对称轴右侧,y随x的增大而____.
y=ax2+k(a≠0) (0,k) 减小
增大
增大
减小
例题讲解
例1
指出下列函数的开口方向、对称轴、顶点坐标及最值.
开口 方向 对称轴 顶点 坐标 最值
向上
向下
(0,4)
(0,-3)
y轴
y轴
当x=0时,有最大值y=4
当 x=0时,有最小值y=-3
例题讲解已知抛物线y=2x2-3.(3)若点 ( -4, y1), ( -1, y2) ,(2, y3)在抛物线y= 2x2-3上,则y1、y2、y3之间的大小关系为(用“<”连接).yx-3336-30y2<y3<y1y1y3y2例2学以致用
1.在同一平面直角坐标系中,不可能由函数 y=2x2+1 的图象通过上下平移变换得到的函数是( )
A.y=2x2- 1 B. y=2x2 C.y=2x2+7 D.y= x2+1
2.将抛物线 y=x2 向上平移1个单位,则平移后的抛物线的解析式为 .
3.抛物线 y=2x2-1 的顶点坐标为( )
A.(2,0) B.(2,1) C. (0,- 1) D. (0,1)
D
y=x2+1
C
学以致用
4.抛物线 y=x2+1 的最低点坐标为 ,
当 x 时,函数有最小值是 .
5.若二次函数 y=(3m-6)x2-1 的开口方向向下,则m的取值范
围是( )A.m> 2 B.m<2 C. m≠2 D. m>一2
6.把抛物线 y=ax2+c 向上平移2个单位,得到抛物线 y=x2,
则 a, c 的值分别是( )
A.1, 2 B.1,﹣2 C.﹣1, 2 D.﹣1,﹣2
(0,1)
=0
1
B
B
7.已知抛物线y=4x2+2上有两点A(x1,y1),B(x2,y2),且x1<x2<0,
则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.无法确定
C
课堂小结
a,k的符号 a>0,k>0 a>0,k<0 a<0,k>0 a<0,k<0
图象
开口方向 对称轴 顶点坐标 函数的增减性 最值 向上
向下
y轴(直线 x=0)
y轴(直线 x=0)
(0,k)
(0,k)
当 x<0 时,y 随 x 增大而减小;当 x>0 时,y 随 x 增大而增大.
当 x<0 时,y 随 x 增大而增大;当 x> 0时,y 随 x 增大而减小.
x=0时,y最小值=k
x=0时,y最大值=k
作业布置
1.教材P41习题22.1第5题(1);
2.见学生用书对应练习.
谢谢
同课章节目录
