2022—2023学年北师大版七年级数学上册1.2展开与折叠同步精练(word版,含答案)
文档属性
| 名称 | 2022—2023学年北师大版七年级数学上册1.2展开与折叠同步精练(word版,含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 280.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-03 21:36:04 | ||
图片预览


文档简介
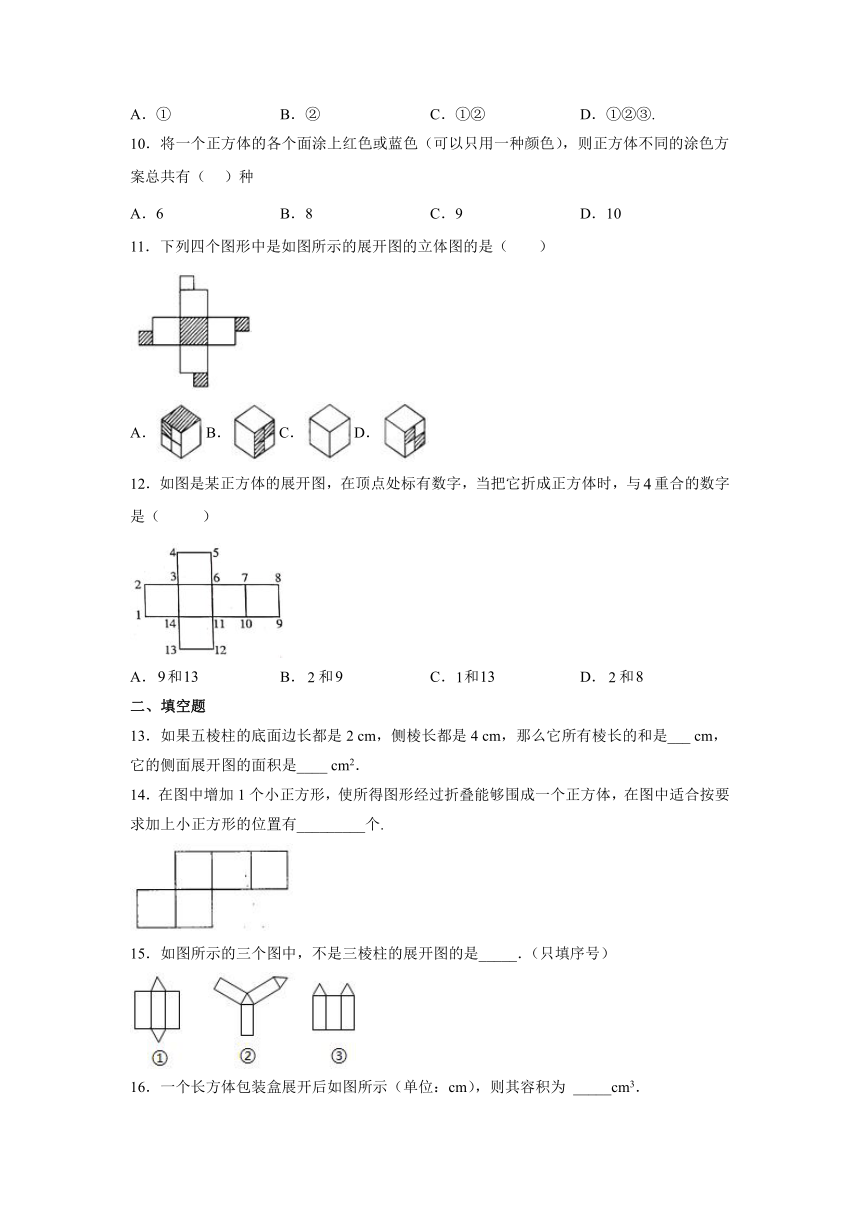
1.2 展开与折叠 同步精练
一、单选题
1.如图为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为( )
A.8 B.12 C.18 D.20
2.如图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( )
A. B. C. D.
3.将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( )
A. B.C.D.
4.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
5.底面半径相等的圆锥与圆柱的高的比为1:3,则圆锥与圆柱的体积的比为( )
A.1:1 B.1:3 C.1:6 D.1:9
6.图(1)的正方体是由图(2)围成的,则图(2)中的“★”标志所在的正方形是正方体中的( )
A.面BCEF B.面CDHE C.面ABFC D.面ADHC
7.下列哪个图形是正方体的展开图( )
A. B. C.D.
8.如图,是一个几何体的表面展开图,则该几何体中写“英”的面相对面上的字是( )
A.战 B.疫 C.情 D.颂
9.如图,线段AB和CD分别是正方体两个面的对角线,将此正方体沿部分棱剪开展开成一个平面图形.观察AB和CD所在的直线,下列情况:①AB⊥CD,②AB∥CD,③AB和CD在同一条直线上,其中可能出现的是( )
A.① B.② C.①② D.①②③.
10.将一个正方体的各个面涂上红色或蓝色(可以只用一种颜色),则正方体不同的涂色方案总共有( )种
A.6 B.8 C.9 D.10
11.下列四个图形中是如图所示的展开图的立体图的是( )
A.B.C.D.
12.如图是某正方体的展开图,在顶点处标有数字,当把它折成正方体时,与重合的数字是( )
A.和 B.和 C.和 D.和
二、填空题
13.如果五棱柱的底面边长都是2 cm,侧棱长都是4 cm,那么它所有棱长的和是___ cm,它的侧面展开图的面积是____ cm2.
14.在图中增加1个小正方形,使所得图形经过折叠能够围成一个正方体,在图中适合按要求加上小正方形的位置有_________个.
15.如图所示的三个图中,不是三棱柱的展开图的是_____.(只填序号)
16.一个长方体包装盒展开后如图所示(单位:cm),则其容积为 _____cm3.
17.如图是一个多面体的表面展开图,则折叠后与棱AB重合的棱是________.
三、解答题
18.如图,是一个正方体纸盒的展开图,请你任选三对非零的互为相反数,分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
19.阅读与思考请阅读下列材料,并完成相应的任务:
包装盒的展开图:如图①是一个同学们熟悉的包装盒如图②是它的一种表面展开图,小明将图②画在如图③所示的的网格中.
(1)在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置是( )
A.字母B;B.字母A;C.字母R;D.字母T
(2)若在图③中,网格中每个小正方形的边长为1,求包装盒的表面积.
20.将如图所示的平面图形折叠后形成的图形的名称依次是________、________、________.
21.探究:有一长6,宽4的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:方案一:以较长的一组对边中点所在直线为轴旋转,如图①;方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)若将此长方形绕着它的其中一条边所在的直线为轴旋转360°,则得到的圆柱体积为多少?
参考答案
1--10AADCD BBBCD 11--12BD
13.40 40
14.4
15.③
16.6000
17.BC
18.第一行1,3,第二行2,,,第三行
19.解:根据长方体展开图的对面间隔一个小长方形,
B与Q是对面,
A与T是对面,
P与R是对面,
∵字母Q表示包装盒的上表面,
∴下表面为B,
故选择A;
(2)解:包装盒的表面积为:2×8+2×1×3=16+6=22.
20.一个长方形和两个圆折叠后,能围成的几何体是圆柱,所以第一个图形为圆柱;
第二个图形折叠后能折成六棱柱;
第三个图形,由一个扇形和一个圆形能围成圆锥.
故答案为 圆柱;六棱柱;圆锥.
21.(1)解:方案一:以较长的一组对边中点所在直线为轴旋转,旋转半径为r=3cm,体积为:cm3,方案二:以较短的一组对边中点所在直线为轴旋转,旋转半径为r=2cm,体积为:cm3,按方案一方法构造的圆柱体积大;
(2)解:分两种情况绕长方形的短边所在的直线为轴旋转360°,得到的圆柱体积为cm3;绕长方形绕长边所在的直线为轴旋转360°,则得到的圆柱体积为cm3,综合将此长方形绕着它的其中一条边所在的直线为轴旋转360°,则得到的圆柱体积为为144 cm3或96 cm3.
一、单选题
1.如图为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为( )
A.8 B.12 C.18 D.20
2.如图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( )
A. B. C. D.
3.将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( )
A. B.C.D.
4.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
5.底面半径相等的圆锥与圆柱的高的比为1:3,则圆锥与圆柱的体积的比为( )
A.1:1 B.1:3 C.1:6 D.1:9
6.图(1)的正方体是由图(2)围成的,则图(2)中的“★”标志所在的正方形是正方体中的( )
A.面BCEF B.面CDHE C.面ABFC D.面ADHC
7.下列哪个图形是正方体的展开图( )
A. B. C.D.
8.如图,是一个几何体的表面展开图,则该几何体中写“英”的面相对面上的字是( )
A.战 B.疫 C.情 D.颂
9.如图,线段AB和CD分别是正方体两个面的对角线,将此正方体沿部分棱剪开展开成一个平面图形.观察AB和CD所在的直线,下列情况:①AB⊥CD,②AB∥CD,③AB和CD在同一条直线上,其中可能出现的是( )
A.① B.② C.①② D.①②③.
10.将一个正方体的各个面涂上红色或蓝色(可以只用一种颜色),则正方体不同的涂色方案总共有( )种
A.6 B.8 C.9 D.10
11.下列四个图形中是如图所示的展开图的立体图的是( )
A.B.C.D.
12.如图是某正方体的展开图,在顶点处标有数字,当把它折成正方体时,与重合的数字是( )
A.和 B.和 C.和 D.和
二、填空题
13.如果五棱柱的底面边长都是2 cm,侧棱长都是4 cm,那么它所有棱长的和是___ cm,它的侧面展开图的面积是____ cm2.
14.在图中增加1个小正方形,使所得图形经过折叠能够围成一个正方体,在图中适合按要求加上小正方形的位置有_________个.
15.如图所示的三个图中,不是三棱柱的展开图的是_____.(只填序号)
16.一个长方体包装盒展开后如图所示(单位:cm),则其容积为 _____cm3.
17.如图是一个多面体的表面展开图,则折叠后与棱AB重合的棱是________.
三、解答题
18.如图,是一个正方体纸盒的展开图,请你任选三对非零的互为相反数,分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
19.阅读与思考请阅读下列材料,并完成相应的任务:
包装盒的展开图:如图①是一个同学们熟悉的包装盒如图②是它的一种表面展开图,小明将图②画在如图③所示的的网格中.
(1)在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置是( )
A.字母B;B.字母A;C.字母R;D.字母T
(2)若在图③中,网格中每个小正方形的边长为1,求包装盒的表面积.
20.将如图所示的平面图形折叠后形成的图形的名称依次是________、________、________.
21.探究:有一长6,宽4的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:方案一:以较长的一组对边中点所在直线为轴旋转,如图①;方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)若将此长方形绕着它的其中一条边所在的直线为轴旋转360°,则得到的圆柱体积为多少?
参考答案
1--10AADCD BBBCD 11--12BD
13.40 40
14.4
15.③
16.6000
17.BC
18.第一行1,3,第二行2,,,第三行
19.解:根据长方体展开图的对面间隔一个小长方形,
B与Q是对面,
A与T是对面,
P与R是对面,
∵字母Q表示包装盒的上表面,
∴下表面为B,
故选择A;
(2)解:包装盒的表面积为:2×8+2×1×3=16+6=22.
20.一个长方形和两个圆折叠后,能围成的几何体是圆柱,所以第一个图形为圆柱;
第二个图形折叠后能折成六棱柱;
第三个图形,由一个扇形和一个圆形能围成圆锥.
故答案为 圆柱;六棱柱;圆锥.
21.(1)解:方案一:以较长的一组对边中点所在直线为轴旋转,旋转半径为r=3cm,体积为:cm3,方案二:以较短的一组对边中点所在直线为轴旋转,旋转半径为r=2cm,体积为:cm3,按方案一方法构造的圆柱体积大;
(2)解:分两种情况绕长方形的短边所在的直线为轴旋转360°,得到的圆柱体积为cm3;绕长方形绕长边所在的直线为轴旋转360°,则得到的圆柱体积为cm3,综合将此长方形绕着它的其中一条边所在的直线为轴旋转360°,则得到的圆柱体积为为144 cm3或96 cm3.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
