2021-2022学年人教版七年级数学上册 2.2 整式的加减 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册 2.2 整式的加减 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 449.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 11:11:06 | ||
图片预览


文档简介
2.2 整式的加减
一、选择题(共10小题)
1. 多项式 可以进一步合并同类项,则 , 的值分别是
A. , B. , C. , D. ,
2. 不一定相等的一组是
A. 与 B. 与
C. 与 D. 与
3. 已知 与 是同类项,则 的值是
A. B. C. D.
4. 下列等式去括号正确的是
A. B.
C. D.
5. 的相反数为
A. B. C. D.
6. 下列各式中去括号正确的是
A.
B.
C.
D.
7. 下列计算中正确的是
A. B. C. D.
8. 已知 ,,则 的值是
A. B. C. D.
9. 某商店在甲批发市场以每包 元的价格进了 包茶叶,又在乙批发市场以每包 元()的价格进了 包同样的茶叶,如果该商店以每包 元的价格卖出这种茶叶,卖完后,这家商店
A. 盈利了 B. 亏损了 C. 不盈不亏 D. 盈亏不能确定
10. 老师设计了接力游戏,用合作的方式完成化简代数式,规则是:每名同学只能利用前面一个同学的式子,进一步计算,再将结果传给下一个同学,最后解决问题.过程如图所示:
接力中,自己负责的一步正确的是
A. 甲 B. 乙 C. 丙 D. 丁
二、填空题(共6小题)
11. 在括号内填上恰当的项:( ).
12. 去括号法则:括号前面是“”号,去掉“”号和括号, ;括号前面是“”号,去掉“”号和括号, .
13. 如图所示的日历中,带阴影的方框里有四个数,随着方框的移动,方框里的四个数存在一定的关系.设最小的一个数为 ,则这四个数之和为 (用含 的代数式表示,并化为最简式).
14. 去括号:
() .
() .
() .
15. 如果 与 是同类项,那么 .
16. 现规定 ,则 的值为 .
三、解答题(共6小题)
17. 判断一个正整数能被 整除的方法是:把这个正整数各个数位上的数字相加,如果所得的和能够被 整除,则这个正整数就能被 整除.请证明对于任意两位正整数,这个判断方法都是正确的.
18. 观察下列各式:
();
();
();
().
探索以上四个式子的变化规律.利用你所探索出来的规律解答下面的题目:
已知:,,求 的值.
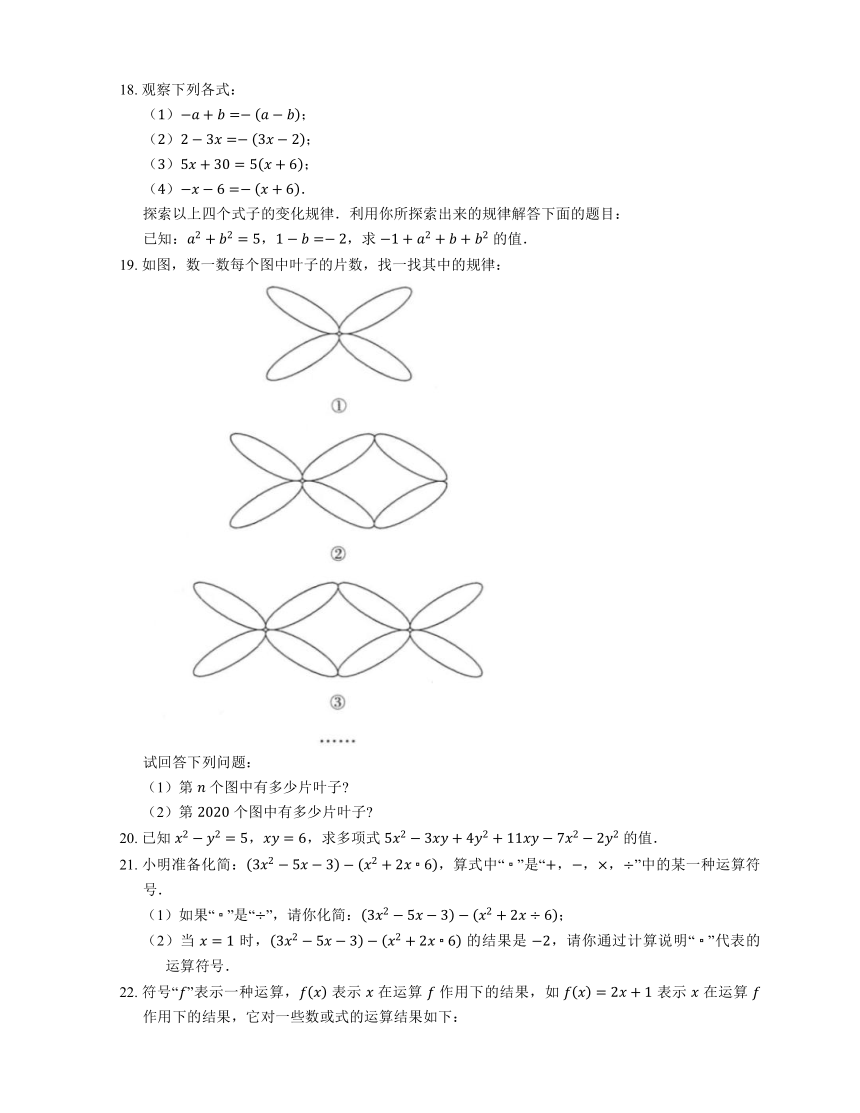
19. 如图,数一数每个图中叶子的片数,找一找其中的规律:
试回答下列问题:
(1)第 个图中有多少片叶子
(2)第 个图中有多少片叶子
20. 已知 ,,求多项式 的值.
21. 小明准备化简:,算式中“”是“,,,”中的某一种运算符号.
(1)如果“”是“”,请你化简:;
(2)当 时, 的结果是 ,请你通过计算说明“”代表的运算符号.
22. 符号“”表示一种运算, 表示 在运算 作用下的结果,如 表示 在运算 作用下的结果,它对一些数或式的运算结果如下:
,,,
利用以上规律计算:
(1).
(2).
答案
1. B
2. D
3. D
4. A
5. D
6. C
7. D
8. A
【解析】当 , 时,
.
9. A
【解析】由题意可得,
,
,
,
卖完后,这家商店盈利了.
10. D
11.
【解析】.
12. 括号里的各项不变号,括号里的各项都变号
13.
14. ,,
15.
16.
【解析】
17. 设这个两位正整数是 .
可以看出, 必定能被 整除,所以判断 能否被 整除,就看 能否被 整除,也就是看它的各位数字之和能否被 整除.
所以,把这个正整数各个数位上的数字相加,如果所得的和能够被 整除,则这个正整数就能被 整除.这个判断方法都是正确的.
18. 规律:把代数式中的某几项添到前面带有“”号的括号内时,添到括号内的项都不改变符号;
添到前面带有“”号的括号内时,添到括号内的项都要改变符号.
当 , 时,
.
19. (1) 观察可知,第 个图中有 片叶子,第 个图中有 片叶子,第 个图中有 片叶子,,则第 个图中有 片叶子.
(2) 由()知,第 个图中有 片叶子.
20. ,.
21. (1) ;
(2) 当 时,,
所以 ,即 ,
所以“”代表的运算符号是“”.
22. (1)
(2)
一、选择题(共10小题)
1. 多项式 可以进一步合并同类项,则 , 的值分别是
A. , B. , C. , D. ,
2. 不一定相等的一组是
A. 与 B. 与
C. 与 D. 与
3. 已知 与 是同类项,则 的值是
A. B. C. D.
4. 下列等式去括号正确的是
A. B.
C. D.
5. 的相反数为
A. B. C. D.
6. 下列各式中去括号正确的是
A.
B.
C.
D.
7. 下列计算中正确的是
A. B. C. D.
8. 已知 ,,则 的值是
A. B. C. D.
9. 某商店在甲批发市场以每包 元的价格进了 包茶叶,又在乙批发市场以每包 元()的价格进了 包同样的茶叶,如果该商店以每包 元的价格卖出这种茶叶,卖完后,这家商店
A. 盈利了 B. 亏损了 C. 不盈不亏 D. 盈亏不能确定
10. 老师设计了接力游戏,用合作的方式完成化简代数式,规则是:每名同学只能利用前面一个同学的式子,进一步计算,再将结果传给下一个同学,最后解决问题.过程如图所示:
接力中,自己负责的一步正确的是
A. 甲 B. 乙 C. 丙 D. 丁
二、填空题(共6小题)
11. 在括号内填上恰当的项:( ).
12. 去括号法则:括号前面是“”号,去掉“”号和括号, ;括号前面是“”号,去掉“”号和括号, .
13. 如图所示的日历中,带阴影的方框里有四个数,随着方框的移动,方框里的四个数存在一定的关系.设最小的一个数为 ,则这四个数之和为 (用含 的代数式表示,并化为最简式).
14. 去括号:
() .
() .
() .
15. 如果 与 是同类项,那么 .
16. 现规定 ,则 的值为 .
三、解答题(共6小题)
17. 判断一个正整数能被 整除的方法是:把这个正整数各个数位上的数字相加,如果所得的和能够被 整除,则这个正整数就能被 整除.请证明对于任意两位正整数,这个判断方法都是正确的.
18. 观察下列各式:
();
();
();
().
探索以上四个式子的变化规律.利用你所探索出来的规律解答下面的题目:
已知:,,求 的值.
19. 如图,数一数每个图中叶子的片数,找一找其中的规律:
试回答下列问题:
(1)第 个图中有多少片叶子
(2)第 个图中有多少片叶子
20. 已知 ,,求多项式 的值.
21. 小明准备化简:,算式中“”是“,,,”中的某一种运算符号.
(1)如果“”是“”,请你化简:;
(2)当 时, 的结果是 ,请你通过计算说明“”代表的运算符号.
22. 符号“”表示一种运算, 表示 在运算 作用下的结果,如 表示 在运算 作用下的结果,它对一些数或式的运算结果如下:
,,,
利用以上规律计算:
(1).
(2).
答案
1. B
2. D
3. D
4. A
5. D
6. C
7. D
8. A
【解析】当 , 时,
.
9. A
【解析】由题意可得,
,
,
,
卖完后,这家商店盈利了.
10. D
11.
【解析】.
12. 括号里的各项不变号,括号里的各项都变号
13.
14. ,,
15.
16.
【解析】
17. 设这个两位正整数是 .
可以看出, 必定能被 整除,所以判断 能否被 整除,就看 能否被 整除,也就是看它的各位数字之和能否被 整除.
所以,把这个正整数各个数位上的数字相加,如果所得的和能够被 整除,则这个正整数就能被 整除.这个判断方法都是正确的.
18. 规律:把代数式中的某几项添到前面带有“”号的括号内时,添到括号内的项都不改变符号;
添到前面带有“”号的括号内时,添到括号内的项都要改变符号.
当 , 时,
.
19. (1) 观察可知,第 个图中有 片叶子,第 个图中有 片叶子,第 个图中有 片叶子,,则第 个图中有 片叶子.
(2) 由()知,第 个图中有 片叶子.
20. ,.
21. (1) ;
(2) 当 时,,
所以 ,即 ,
所以“”代表的运算符号是“”.
22. (1)
(2)
