22.1.3.3 二次函数y=a(x-h)2+k的图象和性质 课件(共22张PPT)
文档属性
| 名称 | 22.1.3.3 二次函数y=a(x-h)2+k的图象和性质 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 247.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 05:49:29 | ||
图片预览






文档简介
(共22张PPT)
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
学习目标
1. 会用描点法画出 y = a(x h)2 + k (a≠0) 的图象;
2. 掌握二次函数 y = a(x h)2 + k (a≠0) 的图象和性质并会应用;(重点)
3. 理解二次函数 y = a(x h)2 + k (a≠0) 与 y = ax2 (a≠0) 之间的联系.(难点)
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
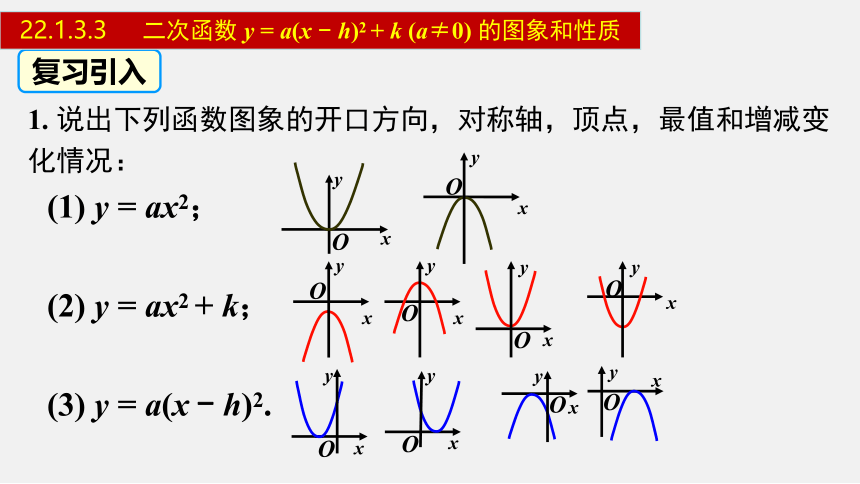
(1) y = ax2;
(2) y = ax2 + k;
(3) y = a(x - h)2.
复习引入
1. 说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:
y
y
y
y
x
x
x
x
O
O
O
O
y
y
y
y
x
x
x
x
O
O
O
O
y
y
x
x
O
O
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
2. 请说出抛物线 y = -2x2 的开口方向、顶点坐标、对称 轴及最值.
3.把 y = -2x2的图象
向上平移3个单位长度
y=-2x2+3
向左平移2个单位长度
y=-2(x+2)2
4. 请猜测一下,二次函数 y = -2(x + 2)2 + 3 的图象是否可以由
y = -2x2 平移得到?学完本课时你就会明白.
开口向上,顶点坐标是 (0,0),对称轴是 y 轴,y最大值 = 0
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
例1 画出函数 的图象,并指出它的开口方向、对称轴和顶点坐标.
探究归纳
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
…
…
…
…
2
1
0
-1
-2
-3
-4
x
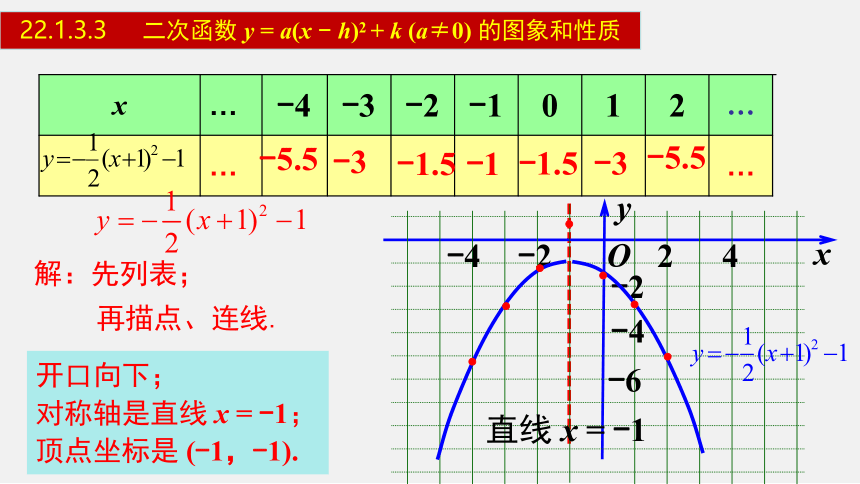
解:先列表;
再描点、连线.
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
2
4
x
-2
-4
-6
y
O
-2
-4
直线 x = -1
开口向下;
对称轴是直线 x = -1;
顶点坐标是 (-1,-1).
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
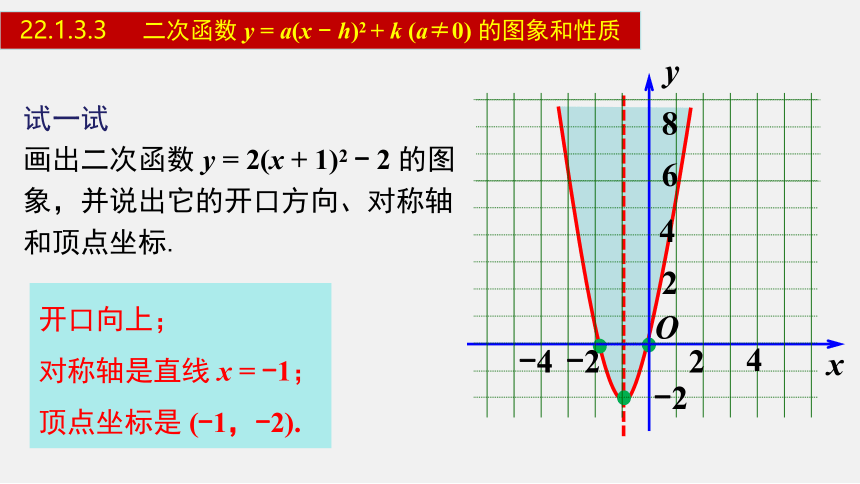
试一试
画出二次函数 y = 2(x + 1)2 - 2 的图象,并说出它的开口方向、对称轴和顶点坐标.
开口向上;
对称轴是直线 x = -1;
顶点坐标是 (-1,-2).
-2
2
x
y
O
-2
4
6
8
-4
2
4
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
二次函数 y = a( x - h )2 + k 的图象和性质
y=a(x-h)2+k a>0 a<0
开口方向 向上 向下
对称轴 直线 x = h 直线 x = h
顶点坐标 (h,k) (h,k)
最值 当 x = h 时,y最小值 = k 当 x = h 时,y最大值 = k
增减性 当 x<h 时,y 随 x 的增大而减小;x>h 时,y 随 x 的增大而增大. 当 x<h 时,y 随 x 的增大而增大;x>h 时,y 随 x 的增大而减小.
知识要点
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
例2 二次函数 y= 2(x + 1)2 4,下列说法正确的是( )
A.图象开口向上
B.图象的对称轴为直线 x=1
C.图象的顶点坐标为 (1,4)
D.当 x< 1 时,y 随 x 的增大而增大
D
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
例3 已知抛物线 y=a(x 3)2 + 2 经过点 (1, 2).
(1)指出抛物线的对称轴;
(2)求 a 的值;
解:(1)由 y=a(x﹣3)2 + 2 可知其顶点为 (3,2),
对称轴为直线 x=3.
(2)∵ 抛物线 y=a(x﹣3)2 + 2 经过点(1,-2),
∴ -2=a(1 - 3)2 + 2,
∴ a=-1.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
(3)若点 A(m,y1)、B(n,y2) (m<n<3) 都在该抛物线上,
试比较 y1 与 y2 的大小.
∴ y1<y2.
解:∵ y=﹣(x﹣3)2 + 2,
∴ 此函数的图象开口向下,
当 x<3 时,y 随 x 的增大而增大.
∵ 点 A(m,y1),B(n,y2) (m<n<3) 都在该抛物线上,
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
探究归纳
例4 怎样移动抛物线 就可以得到抛物线 ?
向左平移1个单位长度
平移方法1
1 个单位长度
向下平移
2
4
x
-2
-4
y
O
-2
-4
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
怎样移动抛物线 可以得到抛物线 ?
平移方法2
向左平移
向下平移
1个单位
1 个单位
2
4
x
-2
-4
y
O
-2
-4
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
知识要点
二次函数 y = ax2 与 y = a(x±h)2±k 的关系
图象的形状和开口方向均相同,可以通过互相平移得到.
y = ax2
y = ax2±k
y = a(x±h)2
y = a( x±h )2±k
上下
平移
左右
平移
上下
平移
左右
平移
平移规律(设 h>0,k>0):
简记为:
上下平移,
常数项上加下减;
左右平移,
自变量左加右减.
二次项系数 a 不变.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
例5 将抛物线 y = 2x2 向左平移 4 个单位长度,再向上平移 1 个单位长度得到的抛物线的解析式为 ( )
A.y = 2(x 4)2 1 B.y = 2(x + 4)2 + 1
C.y = 2(x 4)2 + 1 D.y = 2(x + 4)2 1
B
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
将抛物线 y=5(x﹣1)2 + 1 向上平移 2 个单位长度,再向右平移 3 个单位长度,则所得抛物线的解析式为( )
A.y=5(x + 2)2 + 3 B.y=5(x﹣4)2﹣1
C.y=5(x﹣4)2 + 3 D.y=5(x﹣3)2 + 4
变式训练
C
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
当堂练习
二次函数 开口方向 对称轴 顶点坐标
y = 2(x+3)2+5
向上
(1,-2)
向下
向下
(3,7)
(2,-6)
向上
直线 x = -3
直线 x = 1
直线 x = 3
直线 x = 2
(-3,5)
y =-3(x-1)2-2
y = 4(x-3)2+7
y =-5(2-x)2-6
1. 完成下列表格:
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
2. 抛物线 y = -3x2 + 2 的图象先向右平移 2 个单位长度,再向上平移 1 个单位长度,得到的抛物线解析式为_________________.
3. 抛物线 y = 2x2 不动,把 x 轴、y 轴分别向上、向左平移 3 个单位长度,则在新坐标系下,此抛物线的解析式为_______________.
y = 2(x - 3)2 - 3
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
4. 已知函数 y=﹣(x﹣4)2﹣1.
(3) 怎样移动抛物线 y=﹣x2,就可以得到抛物线
y=﹣(x﹣4)2﹣1
(1) 指出函数图象的开口方向是 ,对称轴是
,顶点坐标为 ;
(2) 当 x 时,y 随 x 的增大而减小;
向下
直线 x=4
(4,﹣1)
>4
解:将抛物线 y=﹣x2 向右平移 4 个单位,再向下平移 1 个单位就可以得到抛物线 y=﹣(x﹣4)2﹣1.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
5. 已知二次函数 y=a(x-1)2-4 的图象经过点 (3,0).
(1) 求 a 的值;
(2) 若 A(m,y1)、B(m+n,y2) (n>0) 是该函数图象上的两点,当 y1=y 2 时,求 m、n 之间的数量关系.
(1) 将 (3,0) 代入 y=a(x-1)2-4, 得 0=4a-4,
(2) 方法一:根据题意,得 y1=(m-1)2-4,y2=(m+n-1)2-4,
∵ y1=y2,
∴ (m-1)2-4=(m+n-1)2-4,即 (m-1)2=(m+n-1)2.
∵ n>0,∴m-1=-(m+n-1),化简,得 2m+n=2.
解:
解得 a=1.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
方法二:
∵ 抛物线 y=a(x-1)2-4 的对称轴是直线 x = 1,
∴ 当 y1=y 2 时,A、B 两点关于直线 x = 1 对称.
∴ ,化简,得 2m+n=2.
要点归纳:对于抛物线 y=a(x-h)2 + k(a≠0) 上的两个不同点 M(x1,y1),N(x2,y2),若 y1 = y2,则必有
,即 x1 + x2 = 2h.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
课堂小结
一般地,抛物线 y = a( x - h )2 + k (a≠0) 与 y = ax2 (a≠0)
的形状相同,位置不同.
二次函数
y = a(x - h)2 + k (a ≠ 0) 的图象和性质
图象特点
当a>0,开口向上;当a<0,开口向下.
对称轴是 x = h,
顶点坐标是 (h,k)
平移规律
左右平移:自变量左加右减;
上下平移:常数项上加下减.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
学习目标
1. 会用描点法画出 y = a(x h)2 + k (a≠0) 的图象;
2. 掌握二次函数 y = a(x h)2 + k (a≠0) 的图象和性质并会应用;(重点)
3. 理解二次函数 y = a(x h)2 + k (a≠0) 与 y = ax2 (a≠0) 之间的联系.(难点)
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
(1) y = ax2;
(2) y = ax2 + k;
(3) y = a(x - h)2.
复习引入
1. 说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:
y
y
y
y
x
x
x
x
O
O
O
O
y
y
y
y
x
x
x
x
O
O
O
O
y
y
x
x
O
O
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
2. 请说出抛物线 y = -2x2 的开口方向、顶点坐标、对称 轴及最值.
3.把 y = -2x2的图象
向上平移3个单位长度
y=-2x2+3
向左平移2个单位长度
y=-2(x+2)2
4. 请猜测一下,二次函数 y = -2(x + 2)2 + 3 的图象是否可以由
y = -2x2 平移得到?学完本课时你就会明白.
开口向上,顶点坐标是 (0,0),对称轴是 y 轴,y最大值 = 0
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
例1 画出函数 的图象,并指出它的开口方向、对称轴和顶点坐标.
探究归纳
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
…
…
…
…
2
1
0
-1
-2
-3
-4
x
解:先列表;
再描点、连线.
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
2
4
x
-2
-4
-6
y
O
-2
-4
直线 x = -1
开口向下;
对称轴是直线 x = -1;
顶点坐标是 (-1,-1).
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
试一试
画出二次函数 y = 2(x + 1)2 - 2 的图象,并说出它的开口方向、对称轴和顶点坐标.
开口向上;
对称轴是直线 x = -1;
顶点坐标是 (-1,-2).
-2
2
x
y
O
-2
4
6
8
-4
2
4
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
二次函数 y = a( x - h )2 + k 的图象和性质
y=a(x-h)2+k a>0 a<0
开口方向 向上 向下
对称轴 直线 x = h 直线 x = h
顶点坐标 (h,k) (h,k)
最值 当 x = h 时,y最小值 = k 当 x = h 时,y最大值 = k
增减性 当 x<h 时,y 随 x 的增大而减小;x>h 时,y 随 x 的增大而增大. 当 x<h 时,y 随 x 的增大而增大;x>h 时,y 随 x 的增大而减小.
知识要点
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
例2 二次函数 y= 2(x + 1)2 4,下列说法正确的是( )
A.图象开口向上
B.图象的对称轴为直线 x=1
C.图象的顶点坐标为 (1,4)
D.当 x< 1 时,y 随 x 的增大而增大
D
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
例3 已知抛物线 y=a(x 3)2 + 2 经过点 (1, 2).
(1)指出抛物线的对称轴;
(2)求 a 的值;
解:(1)由 y=a(x﹣3)2 + 2 可知其顶点为 (3,2),
对称轴为直线 x=3.
(2)∵ 抛物线 y=a(x﹣3)2 + 2 经过点(1,-2),
∴ -2=a(1 - 3)2 + 2,
∴ a=-1.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
(3)若点 A(m,y1)、B(n,y2) (m<n<3) 都在该抛物线上,
试比较 y1 与 y2 的大小.
∴ y1<y2.
解:∵ y=﹣(x﹣3)2 + 2,
∴ 此函数的图象开口向下,
当 x<3 时,y 随 x 的增大而增大.
∵ 点 A(m,y1),B(n,y2) (m<n<3) 都在该抛物线上,
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
探究归纳
例4 怎样移动抛物线 就可以得到抛物线 ?
向左平移1个单位长度
平移方法1
1 个单位长度
向下平移
2
4
x
-2
-4
y
O
-2
-4
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
怎样移动抛物线 可以得到抛物线 ?
平移方法2
向左平移
向下平移
1个单位
1 个单位
2
4
x
-2
-4
y
O
-2
-4
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
知识要点
二次函数 y = ax2 与 y = a(x±h)2±k 的关系
图象的形状和开口方向均相同,可以通过互相平移得到.
y = ax2
y = ax2±k
y = a(x±h)2
y = a( x±h )2±k
上下
平移
左右
平移
上下
平移
左右
平移
平移规律(设 h>0,k>0):
简记为:
上下平移,
常数项上加下减;
左右平移,
自变量左加右减.
二次项系数 a 不变.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
例5 将抛物线 y = 2x2 向左平移 4 个单位长度,再向上平移 1 个单位长度得到的抛物线的解析式为 ( )
A.y = 2(x 4)2 1 B.y = 2(x + 4)2 + 1
C.y = 2(x 4)2 + 1 D.y = 2(x + 4)2 1
B
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
将抛物线 y=5(x﹣1)2 + 1 向上平移 2 个单位长度,再向右平移 3 个单位长度,则所得抛物线的解析式为( )
A.y=5(x + 2)2 + 3 B.y=5(x﹣4)2﹣1
C.y=5(x﹣4)2 + 3 D.y=5(x﹣3)2 + 4
变式训练
C
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
当堂练习
二次函数 开口方向 对称轴 顶点坐标
y = 2(x+3)2+5
向上
(1,-2)
向下
向下
(3,7)
(2,-6)
向上
直线 x = -3
直线 x = 1
直线 x = 3
直线 x = 2
(-3,5)
y =-3(x-1)2-2
y = 4(x-3)2+7
y =-5(2-x)2-6
1. 完成下列表格:
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
2. 抛物线 y = -3x2 + 2 的图象先向右平移 2 个单位长度,再向上平移 1 个单位长度,得到的抛物线解析式为_________________.
3. 抛物线 y = 2x2 不动,把 x 轴、y 轴分别向上、向左平移 3 个单位长度,则在新坐标系下,此抛物线的解析式为_______________.
y = 2(x - 3)2 - 3
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
4. 已知函数 y=﹣(x﹣4)2﹣1.
(3) 怎样移动抛物线 y=﹣x2,就可以得到抛物线
y=﹣(x﹣4)2﹣1
(1) 指出函数图象的开口方向是 ,对称轴是
,顶点坐标为 ;
(2) 当 x 时,y 随 x 的增大而减小;
向下
直线 x=4
(4,﹣1)
>4
解:将抛物线 y=﹣x2 向右平移 4 个单位,再向下平移 1 个单位就可以得到抛物线 y=﹣(x﹣4)2﹣1.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
5. 已知二次函数 y=a(x-1)2-4 的图象经过点 (3,0).
(1) 求 a 的值;
(2) 若 A(m,y1)、B(m+n,y2) (n>0) 是该函数图象上的两点,当 y1=y 2 时,求 m、n 之间的数量关系.
(1) 将 (3,0) 代入 y=a(x-1)2-4, 得 0=4a-4,
(2) 方法一:根据题意,得 y1=(m-1)2-4,y2=(m+n-1)2-4,
∵ y1=y2,
∴ (m-1)2-4=(m+n-1)2-4,即 (m-1)2=(m+n-1)2.
∵ n>0,∴m-1=-(m+n-1),化简,得 2m+n=2.
解:
解得 a=1.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
方法二:
∵ 抛物线 y=a(x-1)2-4 的对称轴是直线 x = 1,
∴ 当 y1=y 2 时,A、B 两点关于直线 x = 1 对称.
∴ ,化简,得 2m+n=2.
要点归纳:对于抛物线 y=a(x-h)2 + k(a≠0) 上的两个不同点 M(x1,y1),N(x2,y2),若 y1 = y2,则必有
,即 x1 + x2 = 2h.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
课堂小结
一般地,抛物线 y = a( x - h )2 + k (a≠0) 与 y = ax2 (a≠0)
的形状相同,位置不同.
二次函数
y = a(x - h)2 + k (a ≠ 0) 的图象和性质
图象特点
当a>0,开口向上;当a<0,开口向下.
对称轴是 x = h,
顶点坐标是 (h,k)
平移规律
左右平移:自变量左加右减;
上下平移:常数项上加下减.
22.1.3.3 二次函数 y = a(x h)2 + k (a≠0) 的图象和性质
同课章节目录
