22.1.4.1 二次函数y=ax2+bx+c的图象和性质 课件(共28张PPT)
文档属性
| 名称 | 22.1.4.1 二次函数y=ax2+bx+c的图象和性质 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 365.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 05:50:40 | ||
图片预览






文档简介
(共28张PPT)
二次函数y=ax +bx+c的图象和性质
22.1.4.1二次函数 y=ax +bx+c的图象和性质
学习目标
1.会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x+h)2+k.(难点)
2.会熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.(重点)
22.1.4.1二次函数 y=ax +bx+c的图象和性质
新课导入
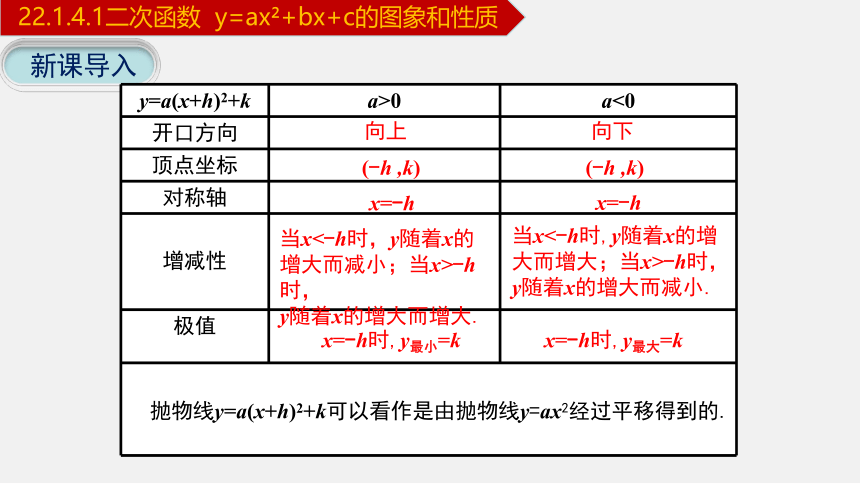
y=a(x+h)2+k a>0 a<0
开口方向
顶点坐标
对称轴
增减性
极值
向上
向下
(-h ,k)
(-h ,k)
x=-h
x=-h
当x<-h时,y随着x的增大而减小;当x>-h时,
y随着x的增大而增大.
当x<-h时,y随着x的增大而增大;当x>-h时,
y随着x的增大而减小.
x=-h时,y最小=k
x=-h时,y最大=k
抛物线y=a(x+h)2+k可以看作是由抛物线y=ax2经过平移得到的.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
新课导入
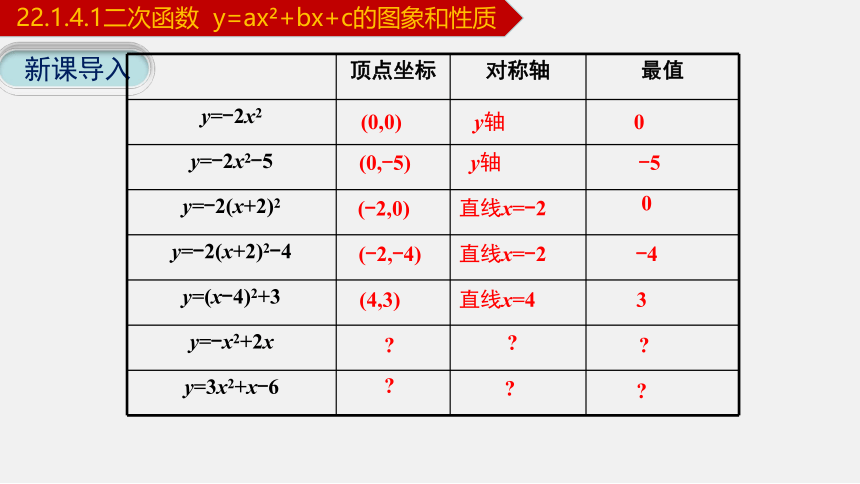
顶点坐标 对称轴 最值
y=-2x2
y=-2x2-5
y=-2(x+2)2
y=-2(x+2)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+x-6
(0,0)
y轴
0
(0,-5)
y轴
-5
(-2,0)
直线x=-2
0
(-2,-4)
直线x=-2
-4
(4,3)
直线x=4
3
22.1.4.1二次函数 y=ax +bx+c的图象和性质
探究归纳
我们已经知道y=a(x+h)2+k的图象和性质,能否利用这些知识来讨论 的图象和性质?
问题1 怎样将 化成y=a(x+h)2+k的形式?
22.1.4.1二次函数 y=ax +bx+c的图象和性质
配方可得
想一想:配方的方法及步骤是什么?
22.1.4.1二次函数 y=ax +bx+c的图象和性质
配方
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
提示:配方后的表达式通常称为配方式或顶点式.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
问题2 你能说出 的对称轴及顶点坐标吗?
答:对称轴是直线x=6,顶点坐标是(6,3).
问题3 二次函数 可以看作是由 怎样平移得到的?
答:平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
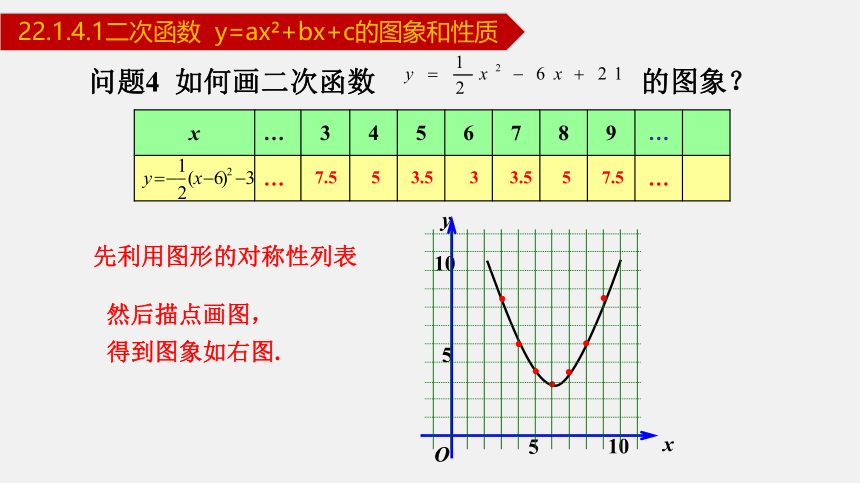
问题4 如何画二次函数 的图象?
…
…
…
…
9
8
7
6
5
4
3
x
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
5
10
x
y
5
10
然后描点画图,
得到图象如右图.
O
22.1.4.1二次函数 y=ax +bx+c的图象和性质
问题5 结合二次函数 的图象,说出其性质.
5
10
x
y
5
10
x=6
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
O
22.1.4.1二次函数 y=ax +bx+c的图象和性质
画出函数 的图象,并说明这个函数具有哪些性质.
x ··· -2 -1 0 1 2 3 4 ···
y ··· ···
-6.5
-4
-2.5
-2
-2.5
-4
-6.5
解: 函数 通过配方可得 ,
先列表:
例1
22.1.4.1二次函数 y=ax +bx+c的图象和性质
2
x
y
-2
0
4
-2
-4
-4
-6
-8
然后描点、连线,得到图象如下图.
由图象可知,这个函数具有如下性质:
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=-2.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).
解:
试一试
22.1.4.1二次函数 y=ax +bx+c的图象和性质
顶点坐标 对称轴 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,3)
x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
( ,-6)
直线x=
练一练
22.1.4.1二次函数 y=ax +bx+c的图象和性质
我们如何用配方法将一般式y=ax2+bx+c(a≠0)化成顶点式y=a(x+h)2+k?
22.1.4.1二次函数 y=ax +bx+c的图象和性质
y=ax +bx+c
22.1.4.1二次函数 y=ax +bx+c的图象和性质
二次函数y=ax2+bx+c的图象和性质
一般地,二次函数y=ax2+bx+c的可以通过配方化成y=a(x+h)2+k的形式,即
因此,抛物线y=ax2+bx+c 的顶点坐标是:
对称轴是:直线
故二次函数y=ax2+bx+c(a≠0)的图象都可以通过二次函数y=ax2的图象平移得到.
归纳总结
22.1.4.1二次函数 y=ax +bx+c的图象和性质
(1)
(2)
x
y
O
x
y
O
二次函数y=ax2+bx+c的图象与性质:
y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
开口方向 向上 向下
顶点坐标
对称轴 直线 直线
22.1.4.1二次函数 y=ax +bx+c的图象和性质
对于二次函数y=ax2+bx+c(c为抛物线与y轴交点的纵坐 标),当c=0时,y=ax2+bx的图象必定经过原点,图象与x轴的另一个交点为
y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
增减性 当 时,y随x的增 大而减小;当 时,y随x的增大而增大 当 时,y随x的增
大而增大;当
时,y随x的增大而减小
最值 当 时,y有最小 值,为 当 时,y有最大
值,为
22.1.4.1二次函数 y=ax +bx+c的图象和性质
已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,
∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,
∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴 ,即b≤1,故选择D .
D
例2
22.1.4.1二次函数 y=ax +bx+c的图象和性质
问题1 一次函数y=kx+b的图象如下图所示,请根据一次函数图象的性质填空:
x
y
O
y=k1x+b1
x
y
O
y=k2x+b2
y=k3x+b3
k1 ___ 0
b1 ___ 0
k2 0
b2 ___ 0
>
>
<
k3 ___ 0
b3 ___ 0
<
>
<
合作探究
22.1.4.1二次函数 y=ax +bx+c的图象和性质
x
y
O
问题2 二次函数 的图象如下图所示,请根据二次函数的性质填空:
a1 ___ 0
b1___ 0
c1___ 0
a2___ 0
b2___ 0
c2___ 0
>
>
>
>
<
=
开口向上,a>0
对称轴在y轴左侧,x<0
对称轴在y轴右侧,x>0
x=0时,y=c.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
x
y
O
a3___ 0
b3___ 0
c3___ 0
a4___ 0
b4___ 0
c4___ 0
<
=
>
<
>
<
开口向下,a<0
对称轴是y轴,x=0
对称轴在y轴右侧,x>0
x=0时,y=c.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
二次函数y=ax2+bx+c的图象与a、b、c的关系
字母符号 图象的特征
a>0 开口__________
a<0 开口__________
b=0 对称轴为_____轴
a、b同号 对称轴在y轴的____侧
a、b异号 对称轴在y轴的____侧
c=0 经过原点
c>0 与y轴交于_____半轴
c<0 与y轴交于_____半轴
向上
向下
y
左
右
正
负
22.1.4.1二次函数 y=ax +bx+c的图象和性质
二次函数y=ax2+bx+c的图象如图,那么abc,2a+b,a+b+c这3个代数式中,值为正数的有( )
A.3个 B.2个 C.1个 D. 0个
∵抛物线的开口向上,∴a>0.
∵对称轴x= >0,∴b<0.
又∵抛物线与y轴的交点在y轴的负半轴上,∴c<0,∴abc>0.
∵x= >1,∴-b>2a,即2a+b<0.
∵当x=1时,抛物线上对应的点在x轴的下方,
∴y=a+b+c<0.
综上所述,abc,2a+b,a+b+c这3个代数式中,值为正数的只有abc.
C
导引:
例3
22.1.4.1二次函数 y=ax +bx+c的图象和性质
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是 ( )
A.1 B.2 C.3 D.4
D
由图象上横坐标为 x=-2的点在第三象限可得4a-2b+c<0,故③正确;
由图象上x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二象限得出 a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.
导引:由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得 c>0,则abc>0,故①正确;
由对称轴x > -1可得2a-b<0,故②正确;
例4
22.1.4.1二次函数 y=ax +bx+c的图象和性质
(1)a决定抛物线的开口方向,简记为“正上负下”;
(2)c决定抛物线与y轴的交点位置,简记为“上正下负原点0”;
(3)a、b的符号共同决定对称轴x= 的位置,简记为:“左同右异y轴0”;可以由各项系数的符号来决定图象的位置,也可以由图象的位置来判断各项系数的符号.
总结
二次函数y=ax2+bx+c的各项系数的符号与图象位置间的关系:
22.1.4.1二次函数 y=ax +bx+c的图象和性质
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
22.1.4.1二次函数 y=ax +bx+c的图象和性质
二次函数y=ax +bx+c的图象和性质
22.1.4.1二次函数 y=ax +bx+c的图象和性质
学习目标
1.会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x+h)2+k.(难点)
2.会熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.(重点)
22.1.4.1二次函数 y=ax +bx+c的图象和性质
新课导入
y=a(x+h)2+k a>0 a<0
开口方向
顶点坐标
对称轴
增减性
极值
向上
向下
(-h ,k)
(-h ,k)
x=-h
x=-h
当x<-h时,y随着x的增大而减小;当x>-h时,
y随着x的增大而增大.
当x<-h时,y随着x的增大而增大;当x>-h时,
y随着x的增大而减小.
x=-h时,y最小=k
x=-h时,y最大=k
抛物线y=a(x+h)2+k可以看作是由抛物线y=ax2经过平移得到的.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
新课导入
顶点坐标 对称轴 最值
y=-2x2
y=-2x2-5
y=-2(x+2)2
y=-2(x+2)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+x-6
(0,0)
y轴
0
(0,-5)
y轴
-5
(-2,0)
直线x=-2
0
(-2,-4)
直线x=-2
-4
(4,3)
直线x=4
3
22.1.4.1二次函数 y=ax +bx+c的图象和性质
探究归纳
我们已经知道y=a(x+h)2+k的图象和性质,能否利用这些知识来讨论 的图象和性质?
问题1 怎样将 化成y=a(x+h)2+k的形式?
22.1.4.1二次函数 y=ax +bx+c的图象和性质
配方可得
想一想:配方的方法及步骤是什么?
22.1.4.1二次函数 y=ax +bx+c的图象和性质
配方
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
提示:配方后的表达式通常称为配方式或顶点式.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
问题2 你能说出 的对称轴及顶点坐标吗?
答:对称轴是直线x=6,顶点坐标是(6,3).
问题3 二次函数 可以看作是由 怎样平移得到的?
答:平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
问题4 如何画二次函数 的图象?
…
…
…
…
9
8
7
6
5
4
3
x
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
5
10
x
y
5
10
然后描点画图,
得到图象如右图.
O
22.1.4.1二次函数 y=ax +bx+c的图象和性质
问题5 结合二次函数 的图象,说出其性质.
5
10
x
y
5
10
x=6
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
O
22.1.4.1二次函数 y=ax +bx+c的图象和性质
画出函数 的图象,并说明这个函数具有哪些性质.
x ··· -2 -1 0 1 2 3 4 ···
y ··· ···
-6.5
-4
-2.5
-2
-2.5
-4
-6.5
解: 函数 通过配方可得 ,
先列表:
例1
22.1.4.1二次函数 y=ax +bx+c的图象和性质
2
x
y
-2
0
4
-2
-4
-4
-6
-8
然后描点、连线,得到图象如下图.
由图象可知,这个函数具有如下性质:
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=-2.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).
解:
试一试
22.1.4.1二次函数 y=ax +bx+c的图象和性质
顶点坐标 对称轴 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,3)
x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
( ,-6)
直线x=
练一练
22.1.4.1二次函数 y=ax +bx+c的图象和性质
我们如何用配方法将一般式y=ax2+bx+c(a≠0)化成顶点式y=a(x+h)2+k?
22.1.4.1二次函数 y=ax +bx+c的图象和性质
y=ax +bx+c
22.1.4.1二次函数 y=ax +bx+c的图象和性质
二次函数y=ax2+bx+c的图象和性质
一般地,二次函数y=ax2+bx+c的可以通过配方化成y=a(x+h)2+k的形式,即
因此,抛物线y=ax2+bx+c 的顶点坐标是:
对称轴是:直线
故二次函数y=ax2+bx+c(a≠0)的图象都可以通过二次函数y=ax2的图象平移得到.
归纳总结
22.1.4.1二次函数 y=ax +bx+c的图象和性质
(1)
(2)
x
y
O
x
y
O
二次函数y=ax2+bx+c的图象与性质:
y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
开口方向 向上 向下
顶点坐标
对称轴 直线 直线
22.1.4.1二次函数 y=ax +bx+c的图象和性质
对于二次函数y=ax2+bx+c(c为抛物线与y轴交点的纵坐 标),当c=0时,y=ax2+bx的图象必定经过原点,图象与x轴的另一个交点为
y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
增减性 当 时,y随x的增 大而减小;当 时,y随x的增大而增大 当 时,y随x的增
大而增大;当
时,y随x的增大而减小
最值 当 时,y有最小 值,为 当 时,y有最大
值,为
22.1.4.1二次函数 y=ax +bx+c的图象和性质
已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,
∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,
∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴 ,即b≤1,故选择D .
D
例2
22.1.4.1二次函数 y=ax +bx+c的图象和性质
问题1 一次函数y=kx+b的图象如下图所示,请根据一次函数图象的性质填空:
x
y
O
y=k1x+b1
x
y
O
y=k2x+b2
y=k3x+b3
k1 ___ 0
b1 ___ 0
k2 0
b2 ___ 0
>
>
<
k3 ___ 0
b3 ___ 0
<
>
<
合作探究
22.1.4.1二次函数 y=ax +bx+c的图象和性质
x
y
O
问题2 二次函数 的图象如下图所示,请根据二次函数的性质填空:
a1 ___ 0
b1___ 0
c1___ 0
a2___ 0
b2___ 0
c2___ 0
>
>
>
>
<
=
开口向上,a>0
对称轴在y轴左侧,x<0
对称轴在y轴右侧,x>0
x=0时,y=c.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
x
y
O
a3___ 0
b3___ 0
c3___ 0
a4___ 0
b4___ 0
c4___ 0
<
=
>
<
>
<
开口向下,a<0
对称轴是y轴,x=0
对称轴在y轴右侧,x>0
x=0时,y=c.
22.1.4.1二次函数 y=ax +bx+c的图象和性质
二次函数y=ax2+bx+c的图象与a、b、c的关系
字母符号 图象的特征
a>0 开口__________
a<0 开口__________
b=0 对称轴为_____轴
a、b同号 对称轴在y轴的____侧
a、b异号 对称轴在y轴的____侧
c=0 经过原点
c>0 与y轴交于_____半轴
c<0 与y轴交于_____半轴
向上
向下
y
左
右
正
负
22.1.4.1二次函数 y=ax +bx+c的图象和性质
二次函数y=ax2+bx+c的图象如图,那么abc,2a+b,a+b+c这3个代数式中,值为正数的有( )
A.3个 B.2个 C.1个 D. 0个
∵抛物线的开口向上,∴a>0.
∵对称轴x= >0,∴b<0.
又∵抛物线与y轴的交点在y轴的负半轴上,∴c<0,∴abc>0.
∵x= >1,∴-b>2a,即2a+b<0.
∵当x=1时,抛物线上对应的点在x轴的下方,
∴y=a+b+c<0.
综上所述,abc,2a+b,a+b+c这3个代数式中,值为正数的只有abc.
C
导引:
例3
22.1.4.1二次函数 y=ax +bx+c的图象和性质
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是 ( )
A.1 B.2 C.3 D.4
D
由图象上横坐标为 x=-2的点在第三象限可得4a-2b+c<0,故③正确;
由图象上x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二象限得出 a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.
导引:由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得 c>0,则abc>0,故①正确;
由对称轴x > -1可得2a-b<0,故②正确;
例4
22.1.4.1二次函数 y=ax +bx+c的图象和性质
(1)a决定抛物线的开口方向,简记为“正上负下”;
(2)c决定抛物线与y轴的交点位置,简记为“上正下负原点0”;
(3)a、b的符号共同决定对称轴x= 的位置,简记为:“左同右异y轴0”;可以由各项系数的符号来决定图象的位置,也可以由图象的位置来判断各项系数的符号.
总结
二次函数y=ax2+bx+c的各项系数的符号与图象位置间的关系:
22.1.4.1二次函数 y=ax +bx+c的图象和性质
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
22.1.4.1二次函数 y=ax +bx+c的图象和性质
同课章节目录
