24.1.1 圆 课件(共26张PPT)
文档属性
| 名称 | 24.1.1 圆 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 06:37:36 | ||
图片预览







文档简介
(共26张PPT)
24.1 圆的有关性质
24.1.1 圆
24.1.1 圆
1. 认识圆,理解圆的本质属性;(重点)
2. 认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、
等弧等与圆有关的概念,并了解它们之间的区别和
联系;(难点)
学习目标
24.1.1 圆
观察下列生活中的图片,找一找你所熟悉的图形.
导入新课
24.1.1 圆
讲授新课
探究圆的概念
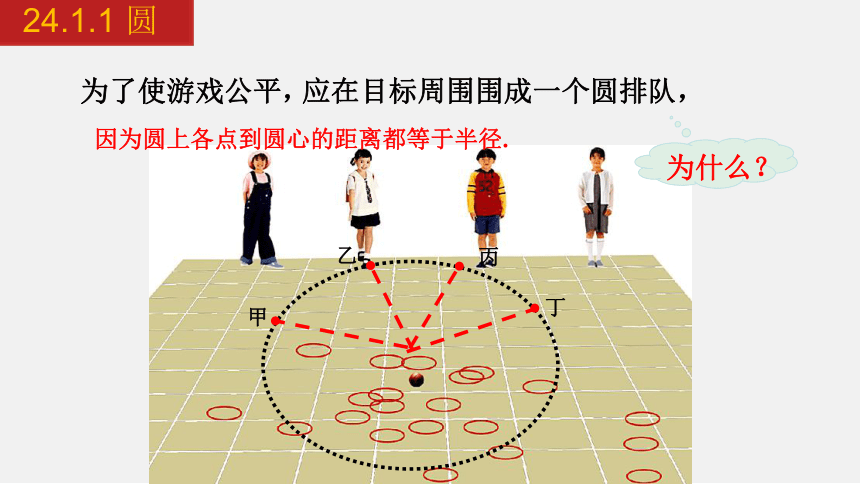
问题1 一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?
24.1.1 圆
甲
丙
乙
丁
为了使游戏公平,
应在目标周围围成一个圆排队,
因为圆上各点到圆心的距离都等于半径.
为什么?
24.1.1 圆
·
r
O
P
圆的旋转定义:
问题2 观察画圆的过程,你能说出圆是如何画出来的吗?
如图,在平面内,线段 OP 绕它固定的一个端点 O 旋转一周,则另一个端点 P 所形成的封闭曲线叫做圆.
固定的端点 O 叫做圆心;
线段 OP 叫做半径;
以点 O 为圆心的圆,记作⊙O,读作“圆O”.
24.1.1 圆
(1)确定一个圆需要两个要素,一是圆心,圆心确定其位置,二是半径,半径确定其大小.
(2)圆是一条封闭的曲线,曲线是“圆周”,而 不能认为是“圆面”.
(3)“圆上的点”指圆周上的点.
要点精析
24.1.1 圆
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
24.1.1 圆
(1) 圆上各点到定点 (圆心O) 的距离都于 .
(2) 平面内到定点 (圆心O) 的距离等于定长(半径r)的所有
点都在 .
由此,我们可以得到圆的集合定义:平面内到定点 (圆心O) 的距离等于定长(半径r)的所有点组成的图形.
O
r
r
r
r
r
定长(半径r)
同一个圆上
想一想:从画圆的过程中,你能说出圆上的点有什么特性吗?
·
24.1.1 圆
例1下列说法中,错误的有( )
(1)经过点P的圆有无数个;
(2)以点P为圆心的圆有无数个;
(3)半径为3 cm且经过点P的圆有无数个;
(4)以点P为圆心,3 cm为半径的圆有无数个.
A.1个 B.2个 C.3个 D.4个
A
导引:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,由此可知(1)(2)正确;(3)半径确定,但圆心不确定,仍有无数个圆;(4)圆心和半径都确定的圆有且只有一个.
典例精析
24.1.1 圆
例2 矩形 ABCD 的对角线 AC、BD 相交于点 O.
求证:A、B、C、D 在以 O 为圆心的同一圆上.
A
B
C
D
O
证明:∵ 四边形 ABCD 是矩形,
∴ AO = OC,OB = OD.
又∵ AC = BD,
∴ OA = OB = OC = OD.
∴ A、B、C、D 在以 O 为圆心,以 OA 为半径的圆上.
典例精析
24.1.1 圆
弦:
·
C
O
A
B
连接圆上任意两点的线段(如图中的 AC)叫做弦.
经过圆心的弦(如图中的 AB)叫做直径.
1. 弦和直径都是线段;
2. 直径是弦,是经过圆心的特殊弦,
但弦不一定 是直径.
注意
圆的有关概念
24.1.1 圆
O
A
B
O
A
B
探索:圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
【发现】直径是最长的弦
24.1.1 圆
知识要点
1. 根据圆的定义,“圆” 指的是 “圆周”,而不是 “圆面”;
2. 直径是圆中最长的弦.
附图解释:
·
C
O
A
B
连接 OC.
在△AOC 中,根据三角形三边关系有 AO + OC>AC,
而 AB = 2OA,AO = OC,所以 AB>AC.
封闭曲线
↗
24.1.1 圆
弧:
·
C
O
A
B
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
半圆
劣弧与优弧
小于半圆的弧叫做劣弧,如图中的 AC ;
大于半圆的弧叫做优弧,如图中的 ABC .
·
C
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧. 以 A、B 为端点的弧记作 ,读作“圆弧 AB”或“弧 AB”.
AB
(
(
(
24.1.1 圆
例3 如图.
(1) 请写出以点 A 为端点的劣弧及优弧;
(2) 请写出以点 A 为端点的弦及直径;
弦 AF,AB,AC. 其中弦 AB 也是直径.
(3) 请任选一条弦,写出这条弦所对的弧.
A
B
C
E
F
D
O
劣弧:
优弧:
答案不唯一,如:弦 AF,它所对的弧是 和 .
24.1.1 圆
等圆:
能够重合的两个圆叫做等圆.
容易看出:
等圆是两个半径相等的圆.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
·
C
O
A
·
C
O1
A
24.1.1 圆
结论:等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
相等“等弧”要区别于“长度的弧”
如图,如果 AB 和 CD 的拉直长度都是 10 cm,移动并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
想一想:长度相等的弧是等弧吗?
24.1.1 圆
例4 如图,在△ABC 中,∠ACB = 90°,∠A = 40°,以 C 为圆心,CB 为半径的圆交 AB 于点 D,连接 CD,
求∠ACD 的度数.
∴∠ACD = 90° - 80° = 10°.
解:∵∠ACB = 90°,∠A = 40°,
∴∠B = 50°.
∵CD = CB,
∴∠BCD = 180° - 2×50° = 80°.
注意
在圆中常利用半径相等得等腰三角形求角度.
24.1.1 圆
例5 以下命题:(1)半圆是弧,但弧不一定是半圆;
(2)过圆上任意一点只能作一条弦,且这条弦是直径;
(3)弦是直径;
(4)直径是圆中最长的弦;
(5)直径不是弦;
(6)优弧大于劣弧;
(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
24.1.1 圆
圆
定义
旋转定义
要画一个确定的圆,关键是确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
半圆
劣弧
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
课堂小结
24.1.1 圆
1. 填空:
(1)______是圆中最长的弦,它是______的 2 倍.
(2)图中有 条直径, 条非直径的弦,
圆中以 A 为一个端点的优弧有 条,劣弧
有 条.
直径
半径
1
2
4
4
当堂练习
A
B
C
D
O
F
E
24.1.1 圆
2. 判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
24.1.1 圆
3.如图,点A,B,C在⊙O上,点O在线段AC上,点
D在线段AB上,下列说法正确的是( )
A.线段AB,AC,CD,OB都是弦
B.与线段OB相等的线段有OA,OC,CD
C.图中的优弧有2条
D.AC是弦,AC又是⊙O的直径,所以弦是直径
C
24.1.1 圆
4. 如图,AB 是⊙O 的直径,点 C、D 在⊙O 上,且点 C、D 在 AB 的异侧,连接 AD、OD、OC.若∠AOC = 70°,且 AD∥OC,求∠AOD 的度数.
解:∵AD∥OC,
∴∠DAO =∠AOC = 70°.
又∵OD = OA,
∴∠ADO =∠DAO = 70°.
∴∠AOD = 180-70°-70° = 40°.
24.1.1 圆
5.已知:如图,在⊙O中,AB为弦,C、D两点在 AB上,且AC=BD.
求证:OC=OD.
证明:∵OA、OB为⊙O的半径,
∴OA=OB. ∴∠A=∠B.
又∵AC=BD,
∴△ACO≌△BDO. ∴OC=OD.
24.1.1 圆
24.1 圆的有关性质
24.1.1 圆
24.1.1 圆
1. 认识圆,理解圆的本质属性;(重点)
2. 认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、
等弧等与圆有关的概念,并了解它们之间的区别和
联系;(难点)
学习目标
24.1.1 圆
观察下列生活中的图片,找一找你所熟悉的图形.
导入新课
24.1.1 圆
讲授新课
探究圆的概念
问题1 一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?
24.1.1 圆
甲
丙
乙
丁
为了使游戏公平,
应在目标周围围成一个圆排队,
因为圆上各点到圆心的距离都等于半径.
为什么?
24.1.1 圆
·
r
O
P
圆的旋转定义:
问题2 观察画圆的过程,你能说出圆是如何画出来的吗?
如图,在平面内,线段 OP 绕它固定的一个端点 O 旋转一周,则另一个端点 P 所形成的封闭曲线叫做圆.
固定的端点 O 叫做圆心;
线段 OP 叫做半径;
以点 O 为圆心的圆,记作⊙O,读作“圆O”.
24.1.1 圆
(1)确定一个圆需要两个要素,一是圆心,圆心确定其位置,二是半径,半径确定其大小.
(2)圆是一条封闭的曲线,曲线是“圆周”,而 不能认为是“圆面”.
(3)“圆上的点”指圆周上的点.
要点精析
24.1.1 圆
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
24.1.1 圆
(1) 圆上各点到定点 (圆心O) 的距离都于 .
(2) 平面内到定点 (圆心O) 的距离等于定长(半径r)的所有
点都在 .
由此,我们可以得到圆的集合定义:平面内到定点 (圆心O) 的距离等于定长(半径r)的所有点组成的图形.
O
r
r
r
r
r
定长(半径r)
同一个圆上
想一想:从画圆的过程中,你能说出圆上的点有什么特性吗?
·
24.1.1 圆
例1下列说法中,错误的有( )
(1)经过点P的圆有无数个;
(2)以点P为圆心的圆有无数个;
(3)半径为3 cm且经过点P的圆有无数个;
(4)以点P为圆心,3 cm为半径的圆有无数个.
A.1个 B.2个 C.3个 D.4个
A
导引:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,由此可知(1)(2)正确;(3)半径确定,但圆心不确定,仍有无数个圆;(4)圆心和半径都确定的圆有且只有一个.
典例精析
24.1.1 圆
例2 矩形 ABCD 的对角线 AC、BD 相交于点 O.
求证:A、B、C、D 在以 O 为圆心的同一圆上.
A
B
C
D
O
证明:∵ 四边形 ABCD 是矩形,
∴ AO = OC,OB = OD.
又∵ AC = BD,
∴ OA = OB = OC = OD.
∴ A、B、C、D 在以 O 为圆心,以 OA 为半径的圆上.
典例精析
24.1.1 圆
弦:
·
C
O
A
B
连接圆上任意两点的线段(如图中的 AC)叫做弦.
经过圆心的弦(如图中的 AB)叫做直径.
1. 弦和直径都是线段;
2. 直径是弦,是经过圆心的特殊弦,
但弦不一定 是直径.
注意
圆的有关概念
24.1.1 圆
O
A
B
O
A
B
探索:圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
【发现】直径是最长的弦
24.1.1 圆
知识要点
1. 根据圆的定义,“圆” 指的是 “圆周”,而不是 “圆面”;
2. 直径是圆中最长的弦.
附图解释:
·
C
O
A
B
连接 OC.
在△AOC 中,根据三角形三边关系有 AO + OC>AC,
而 AB = 2OA,AO = OC,所以 AB>AC.
封闭曲线
↗
24.1.1 圆
弧:
·
C
O
A
B
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
半圆
劣弧与优弧
小于半圆的弧叫做劣弧,如图中的 AC ;
大于半圆的弧叫做优弧,如图中的 ABC .
·
C
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧. 以 A、B 为端点的弧记作 ,读作“圆弧 AB”或“弧 AB”.
AB
(
(
(
24.1.1 圆
例3 如图.
(1) 请写出以点 A 为端点的劣弧及优弧;
(2) 请写出以点 A 为端点的弦及直径;
弦 AF,AB,AC. 其中弦 AB 也是直径.
(3) 请任选一条弦,写出这条弦所对的弧.
A
B
C
E
F
D
O
劣弧:
优弧:
答案不唯一,如:弦 AF,它所对的弧是 和 .
24.1.1 圆
等圆:
能够重合的两个圆叫做等圆.
容易看出:
等圆是两个半径相等的圆.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
·
C
O
A
·
C
O1
A
24.1.1 圆
结论:等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
相等“等弧”要区别于“长度的弧”
如图,如果 AB 和 CD 的拉直长度都是 10 cm,移动并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
想一想:长度相等的弧是等弧吗?
24.1.1 圆
例4 如图,在△ABC 中,∠ACB = 90°,∠A = 40°,以 C 为圆心,CB 为半径的圆交 AB 于点 D,连接 CD,
求∠ACD 的度数.
∴∠ACD = 90° - 80° = 10°.
解:∵∠ACB = 90°,∠A = 40°,
∴∠B = 50°.
∵CD = CB,
∴∠BCD = 180° - 2×50° = 80°.
注意
在圆中常利用半径相等得等腰三角形求角度.
24.1.1 圆
例5 以下命题:(1)半圆是弧,但弧不一定是半圆;
(2)过圆上任意一点只能作一条弦,且这条弦是直径;
(3)弦是直径;
(4)直径是圆中最长的弦;
(5)直径不是弦;
(6)优弧大于劣弧;
(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
24.1.1 圆
圆
定义
旋转定义
要画一个确定的圆,关键是确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
半圆
劣弧
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
课堂小结
24.1.1 圆
1. 填空:
(1)______是圆中最长的弦,它是______的 2 倍.
(2)图中有 条直径, 条非直径的弦,
圆中以 A 为一个端点的优弧有 条,劣弧
有 条.
直径
半径
1
2
4
4
当堂练习
A
B
C
D
O
F
E
24.1.1 圆
2. 判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
24.1.1 圆
3.如图,点A,B,C在⊙O上,点O在线段AC上,点
D在线段AB上,下列说法正确的是( )
A.线段AB,AC,CD,OB都是弦
B.与线段OB相等的线段有OA,OC,CD
C.图中的优弧有2条
D.AC是弦,AC又是⊙O的直径,所以弦是直径
C
24.1.1 圆
4. 如图,AB 是⊙O 的直径,点 C、D 在⊙O 上,且点 C、D 在 AB 的异侧,连接 AD、OD、OC.若∠AOC = 70°,且 AD∥OC,求∠AOD 的度数.
解:∵AD∥OC,
∴∠DAO =∠AOC = 70°.
又∵OD = OA,
∴∠ADO =∠DAO = 70°.
∴∠AOD = 180-70°-70° = 40°.
24.1.1 圆
5.已知:如图,在⊙O中,AB为弦,C、D两点在 AB上,且AC=BD.
求证:OC=OD.
证明:∵OA、OB为⊙O的半径,
∴OA=OB. ∴∠A=∠B.
又∵AC=BD,
∴△ACO≌△BDO. ∴OC=OD.
24.1.1 圆
同课章节目录
